Дополнительные комментарии и объяснения:
«ГДЗшник.ru» не только предлагает готовые ответы, но и дает дополнительные комментарии и объяснения к решениям. Это позволяет лучше понять материал, исправить ошибки и запомнить правильный подход к задачам. Таким образом, сервис становится не только инструментом для проверки, но и обучающим ресурсом.
Итак, если вам нужно быстро и бесплатно найти решения домашних заданий, обратитесь к сервису «ГДЗшник.ру». Удобство использования, бесплатность, актуальность информации и дополнительные комментарии делают этот ресурс отличным помощником для школьников. Не теряйте времени на поиски — «ГДЗшник.ру» поможет вам успешно справиться с учебными заданиями!
На ГДЗшник.ru вы найдете не только готовые ответы, но и подробные разъяснения к ним, что поможет вам глубже понять учебный материал и успешно справиться с домашними заданиями. Не забывайте использовать ГДЗ как инструмент для обучения и развития, а не как способ легкого пути к решению задач.
Проверь себя
Задание 1. Что такое окружность?
- Замкнутая кривая, все точки которой равноудалены от центра;
- Геометрическая фигура, которая ограничена замкнутой кривой, все точки которой равноудалены от центра;
- Геометрическая фигура, которая имеет круглую форму;
- Часть плоскости, ограниченная замкнутой кривой, все точки которой равноудалены от центра.
Задание 2. Что такое диаметр окружности?
- Это отрезок, соединяющий центр окружности и любую точку на окружности;
- Это отрезок, соединяющий две произвольные точки на окружности;
- Это отрезок, соединяющий две точки на окружности и проведенный через центр окружности;
- Это половина дуги окружности.
Задание 3.По какой формуле можно найти длину окружности?
- \(l = \frac{R}{180} * n\)
- \(C=2 \pi R\)
- C=2R
- \(l = \pi R\)
Задание 4. На окружности выделили дугу в 60 градусов. Какую часть от всей окружности занимает эта дуга?
- \(\frac{1}{2}\)
- \(\frac{1}{3}\)
- \(\frac{1}{6}\)
- \(\frac{1}{4}\)
Задание 5. Вписанный угол равен 50 градусов. Чему равен центральный угол, опирающийся на ту же дугу?
- 200
- 50
- 100
- 150
Ответы: 1. – 1 2. – 3 3. – 2 4. – 3 5. – 3
Вычитание числа из суммы
Страница 28 — 29
1. Расставь скобки так, чтобы записи стали верными.
Решение: 63 - (30 + 3) = 30 18 : (6:3) = 9 (44 + 6) * 2 = 100 35 - (30 + 5) = 0 16 - (10 - 6) = 12 3 * (6 + 14) = 60
2. Выполни действия.
Решение:
3. Велосипедист спешит на станцию. Помоги ему найти самую короткую дорогу, ответ числовой цепочки на которой будет меньше остальных. Обведи эту дорогу красным цветом и напиши ответ в пустом окошке.
Решение:
4. В мешке было 30 кг муки. После того как за 3 дня израсходовали несколько килограммов муки (во все дни поровну), в мешке осталось 18 кг муки. По скольку килограммов муки расходовали каждый день? Реши задачу выражением.
Решение: (30 - 18) : 3 = 4 (кг) Ответ: каждый день расходовали по 4 кг муки.
5. Разгадай закономерность, по которой записаны числа в кружках и квадратах. Заполни пропуски нужными числами.
Решение:
6. Для поездки в летний лагерь на вокзал приехали дети. Из них 47 мальчиков, а остальные девочки. Все дети разместились в трёх автобусах, по 30 человек в каждом. Сколько было девочек? Реши задачу выражением.
Решение: 30 * 3 - 47 = 43 (д.) Ответ: в лагерь поехало 43 девочки.
7. На пунктирной линии начерти отрезок OL в 2 раза короче данного отрезка SK.
Решение: SK = 10 см OL = 5 см Ответ: длина отрезка OL - 5 см.
8. В двух залах музея было 54 человек. Когда в первый зал пришли еще 9 человек, а во второй — 7 человек, то в залах людей стало поровну. Сколько человек в каждом зале первоначально?
Решение: Пусть в 1 зале - Х человек, тогда во втором зале - (54 - Х) человек. Тогда по условию задачи получаем, следующее равенство: X + 9 = (54 - X) + 7 X + 9 - 54 - Х + 7 2 X = 54 + 7 - 9 2 X = 52 X = 26 (ч.) - в первом зале. Тогда во втором зале: 54 - 26 = 28 (ч.) Ответ: в первом зале было 26 человек, а во втором 28 человек.
Часть 1:
стр. 4
стр. 5
стр. 6
стр. 7
стр. 8
стр. 9
стр. 10
стр. 11
стр. 12
стр. 13
стр. 14
стр. 15
стр. 16
стр. 18
стр. 19
стр. 20
стр. 21
стр. 22
стр. 23
стр. 24
стр. 25
стр. 26
стр. 27
стр. 28
стр. 29
стр. 30
стр. 31
стр. 32
стр. 33
стр. 34
стр. 35
стр. 36
стр. 37
стр. 38
стр. 39
стр. 40
стр. 41
стр. 42
стр. 43
стр. 44
стр. 45
стр. 46
стр. 47
стр. 48
стр. 49
стр. 52
стр. 53
стр. 54
стр. 55
стр. 57
стр. 58
стр. 59
стр. 60
стр. 61
стр. 62
стр. 63
стр. 64
стр. 65
стр. 66
стр. 67
стр. 68
стр. 69
стр. 70
стр. 71
стр. 72
стр. 73
стр. 74
стр. 75
стр. 76
стр. 77
стр. 78
стр. 79
стр. 80
стр. 81
стр. 82
стр. 83
стр. 84
стр. 85
стр. 86
стр. 87
стр. 88
стр. 89
стр. 90
стр. 92
стр. 93
стр. 94
стр. 95
стр. 96
стр. 97
стр. 98
стр. 99
стр. 100
стр. 101
стр. 102
стр. 103
стр. 104
стр. 105
стр. 106
стр. 107
стр. 108
стр. 109
стр. 110
стр. 111
Числа от 0 до 100 (повторение)
Страница 4 -5
1. Восстанови записи.
Решение:
46=40+6 70=10+60 68=75-7 89=90-1 91=90+1 30=50-20 14=53-39 50=0+50 28=30-2 55=60-5 29=54-25 36=36-0
2. Запиши числа в порядке возрастания:
49, 90, 44, 9, 50, 99, 40, 95, 59, 55, 94
Решение:
9, 40, 44, 49, 50, 55, 59, 90, 94, 95, 99
3. Сравни.
Решение:
5 дм 4 см > 53 см 1 м 8 дм < 81 дм 3 м < 31 дм 2 дм 8 см < 30 см 4 м 1 дм > 40 дм 7 дм > 69 см
4. Выдели прямоугольной рамкой те числа, сумма которых равна 80.
Решение:
5. Длина прямоугольника равна 10 см, а ширина 6 см. Найди периметр этого прямоугольника.
Решение: 10 + 6 + 10 + 6 = 32 (см) Ответ: периметр прямоугольника равен 32 см.
6. Выполни вычисления. Прочитай загадку, записав в таблицы под значениями выражений соответствующие части слов. Отгадай ее и запиши отгадку.
Решение:
В результате вычислений получилась загадка: крашеное коромысло через реку повисло.
Отгадка: радуга.
7. Заполни пропуски и реши взаимно обратные задачи.
| Было — 60 р. Потратили — 19 р. Осталось — ?Решение:60 — 19 = 41 (р.)Ответ: 41 р. | Было — ? Потратили — 19 р. Осталось — 41 р.Решение:19 + 41 = 60 (р.)Ответ: 60 р. | Было — 60 р. Потратили — ? Осталось — 41 р.Решение:60 — 41 = 19 (р.)Ответ: 19 р. |
8. Запиши, сколько времени показывают каждые часы.
| 1 ч 20 мин | 10 ч 15 мин | 17 ч 55 мин |
Страница 6 — 7
9. Выполни действия.
Решение:
10. Расшифруй старинное русское название прямоугольника. Для этого выполни вычисления и запиши в таблицы под значениями выражений соответствующие буквы.
Решение:
Ответ: старинное русское название прямоугольника — решётка долгая.
11. Зачеркни лишнее выражение под каждым рисунком. Запиши в ответе количество кругов на рисунке.
Решение:
12. Реши задачи.
1) В магазин привезли яблоки и груши. Яблок было 20 ящиков, а груш — в 4 раза меньше. Сколько ящиков груш привезли в магазин?
Решение: 20 : 4 = 5 (ящ.) Ответ: 5 ящиков груш привезли в магазин.
2) Длина одной из сторон прямоугольника 49 м, а другая сторона в 2 раза длиннее. Найди длину другой стороны прямоугольника.
Решение: 49 * 2 = 98 (м.) Ответ: длина другой стороны прямоугольника 98 метров.
3) Дочке 10 лет, а мама в 3 раза старше дочки. Сколько лет маме?
Решение: 10 * 3 = 30 (л.) Ответ: маме 30 лет.
4) На выполнение домашней работы по математике Саша потратил 23 мин, а Лена на 5 мин меньше. За сколько минут Лена выполнила домашнюю работу по математике?
Решение: 23 - 5 = 18 (мин.) Ответ: Лена выполнила домашнюю работу по математике за 18 минут.
13. Сравни.
Решение:
78 - 35 > 80 - 40 23 + 47 = 30 + 40 96 - 50 < 9 + 65 73 - 2 > 73 - 20
14. Построй другой прямоугольник с таким же периметром.
Решение: Найдем периметр прямоугольника АБСД 3 + 3 + 3 + 3 = 12 см
Углы в окружности
Центральный угол – это угол, вершина которого лежит в центре окружности. При этом угол опирается на дугу окружности.
На рисунке угол АОВ будет центральным.
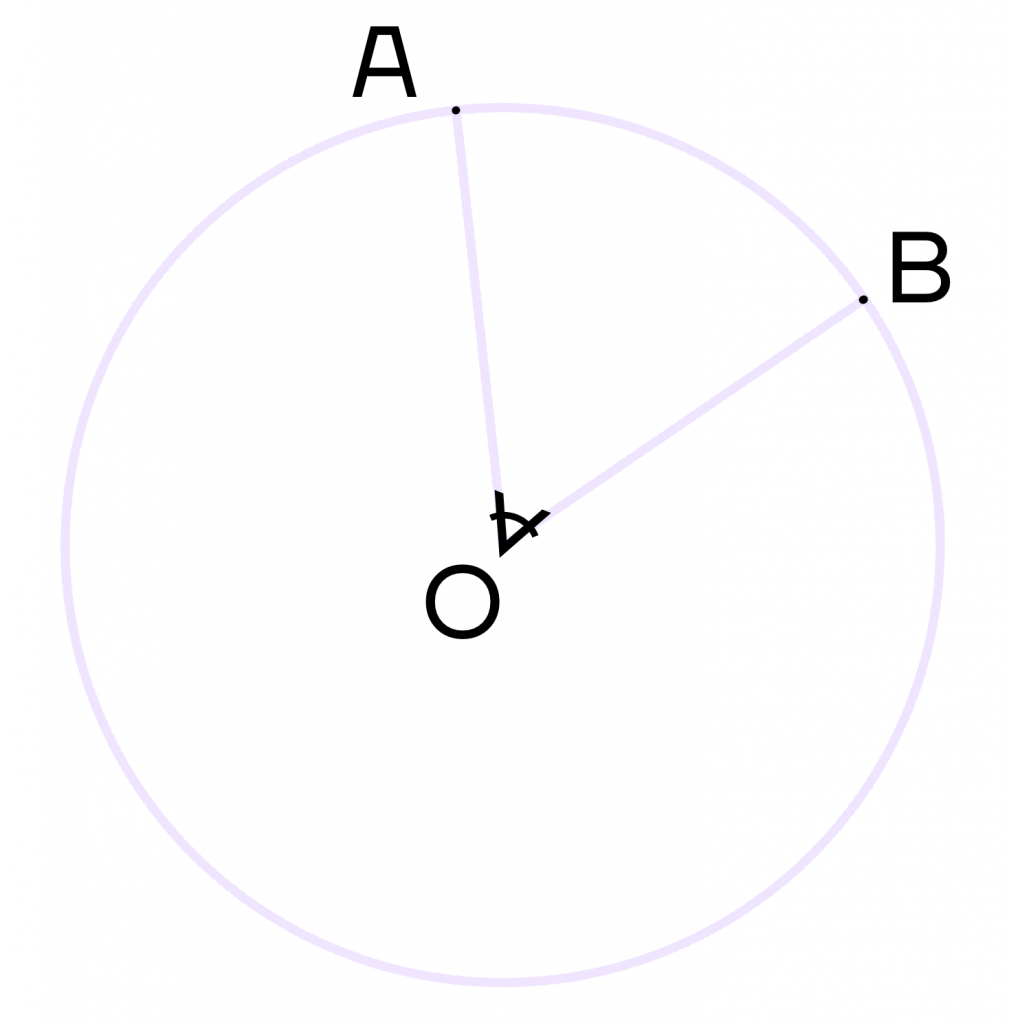
Свойство центрального угла:
Центральный угол равен градусной мере дуги, на которую он опирается.
Например, дуга АВ равна 36\(\circ\), тогда угол АОВ также равен 36\(\circ\).
Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол также должен опираться на дугу окружности.
На рисунке угол АСВ – вписанный.
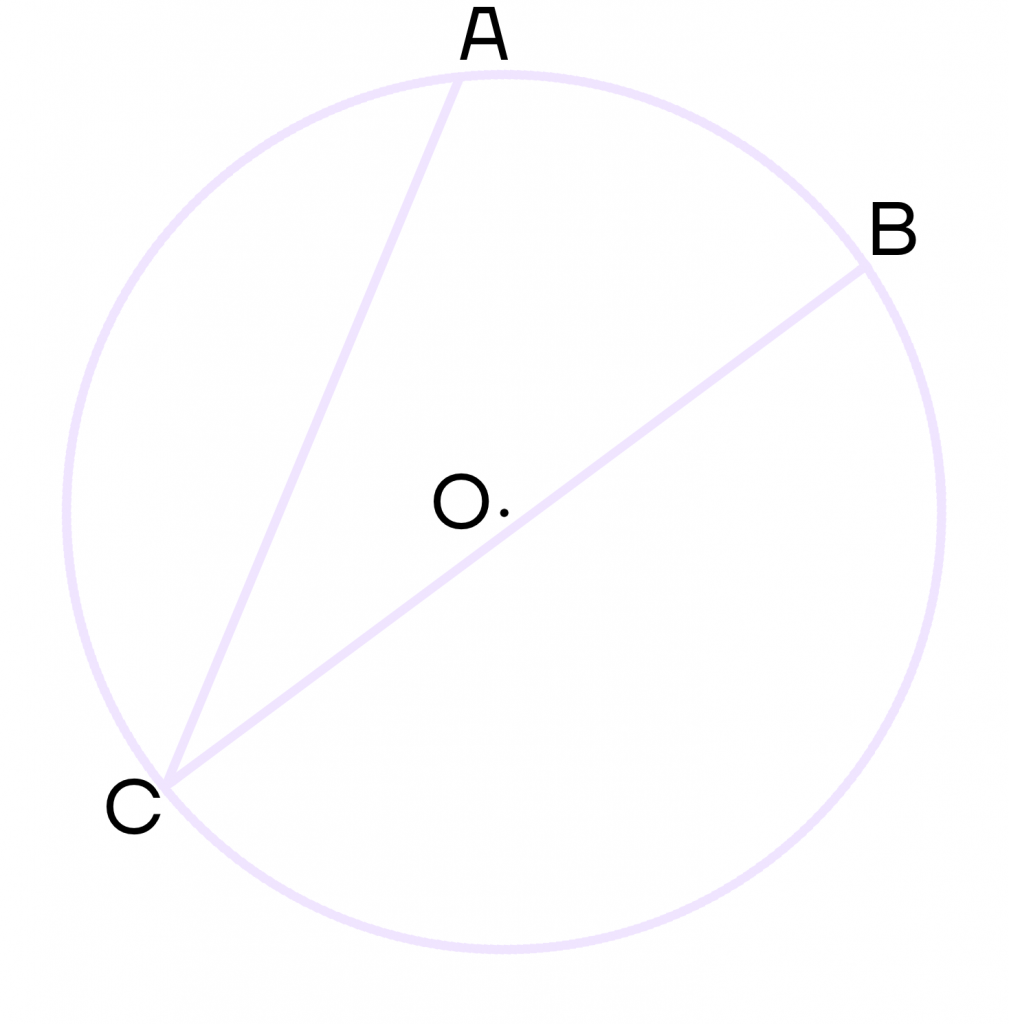
Свойства вписанного угла окружности:
Вписанный угол равен половине градусной меры дуги, на которую он опирается.
Например, дуга АВ равна 50\(\circ\), тогда угол АСВ равен 25\(\circ\).
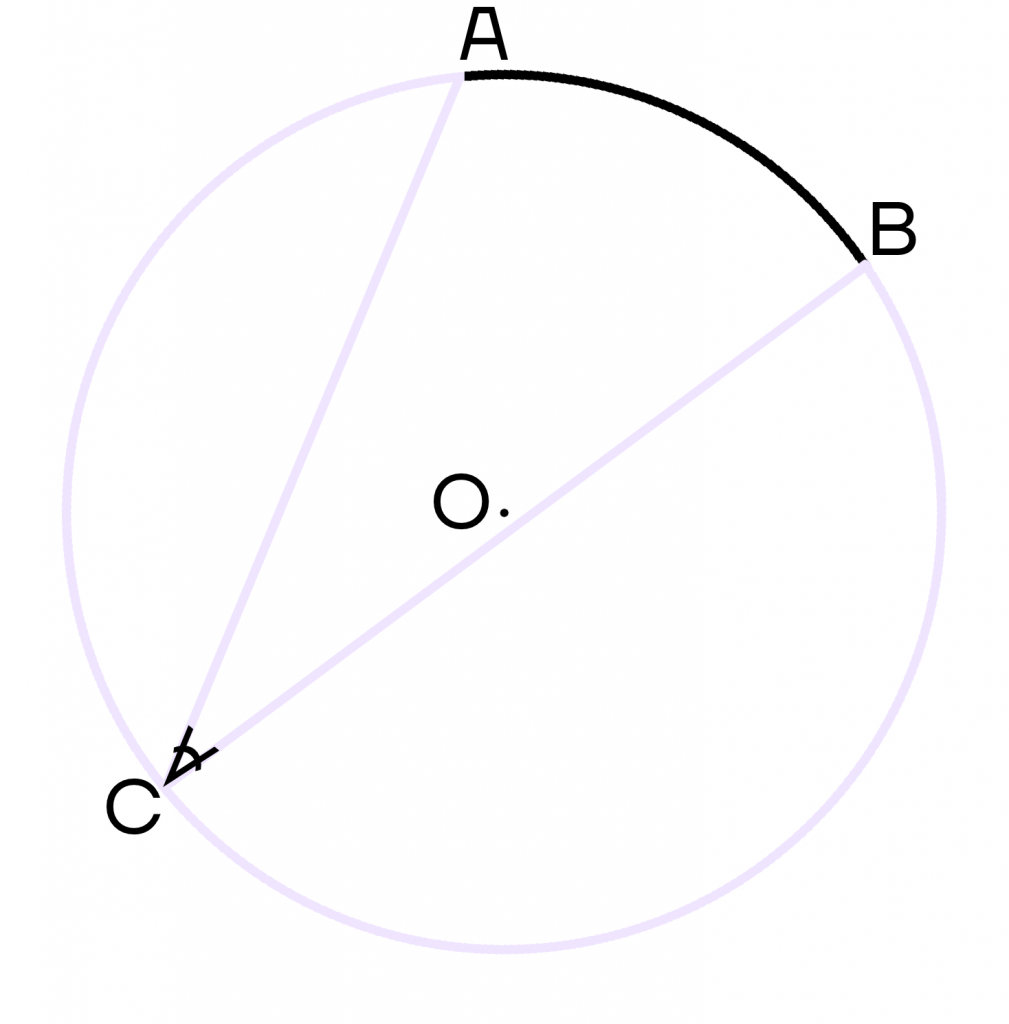
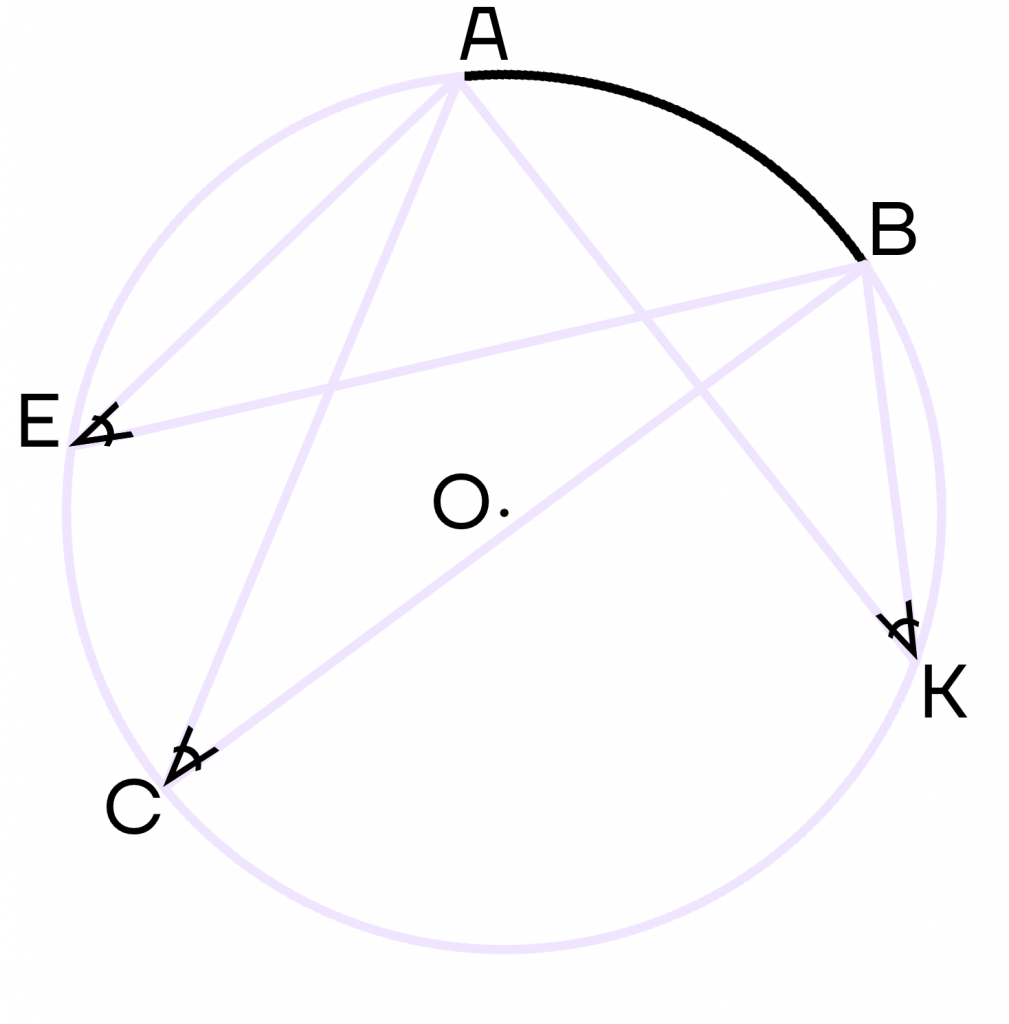
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Пусть углы АСВ, АЕВ и АКВ опираются на душу АВ. Тогда эти углы будут равны между собой.
Вписанный угол, опирающийся на диаметр, равен 90\(\circ\).
Вспомним, что диаметр делит окружность на две полуокружности, градусные меры которых равны 180\(\circ\). Тогда вписанный угол будет равняться 180\(\circ\) : 2 = 90\(\circ\).
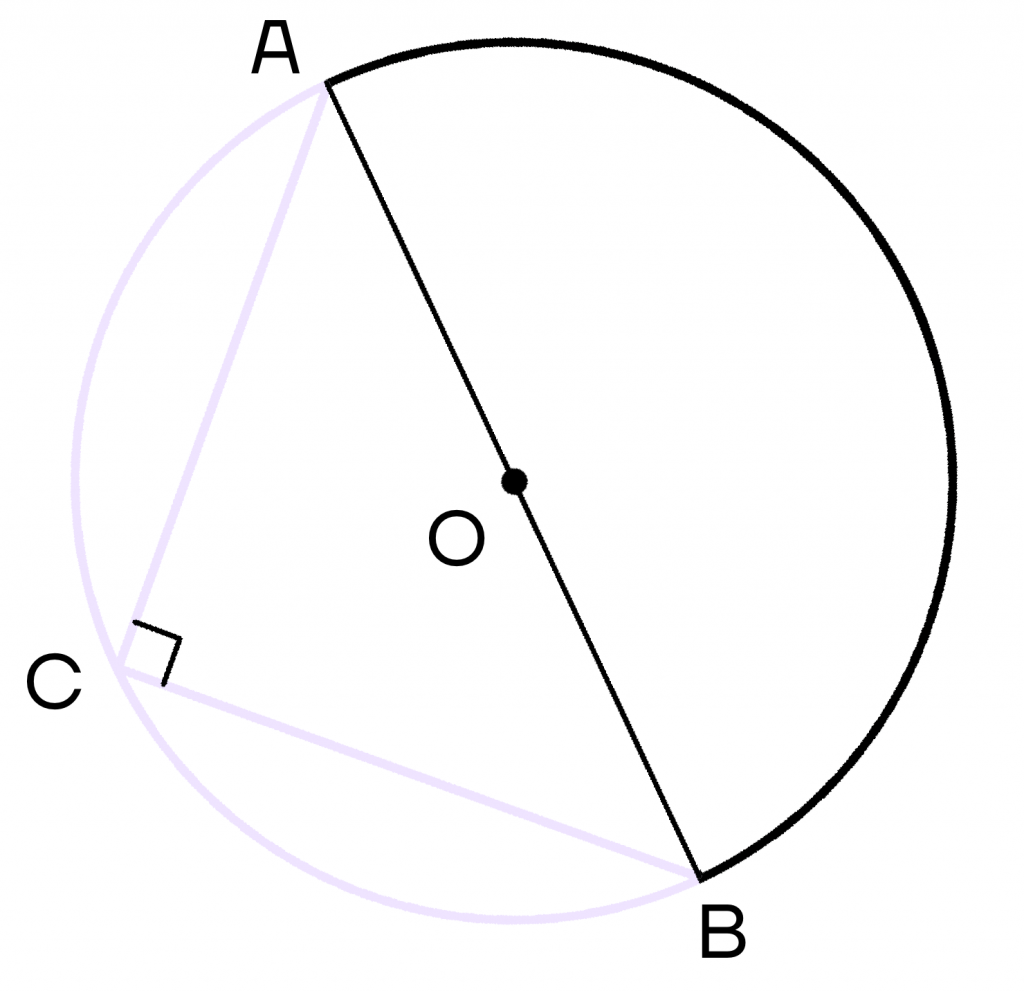
Также важно заметить, что вписанный угол равен половине центрального угла. При этом данные углы обязательно должны опираться на одну дугу.
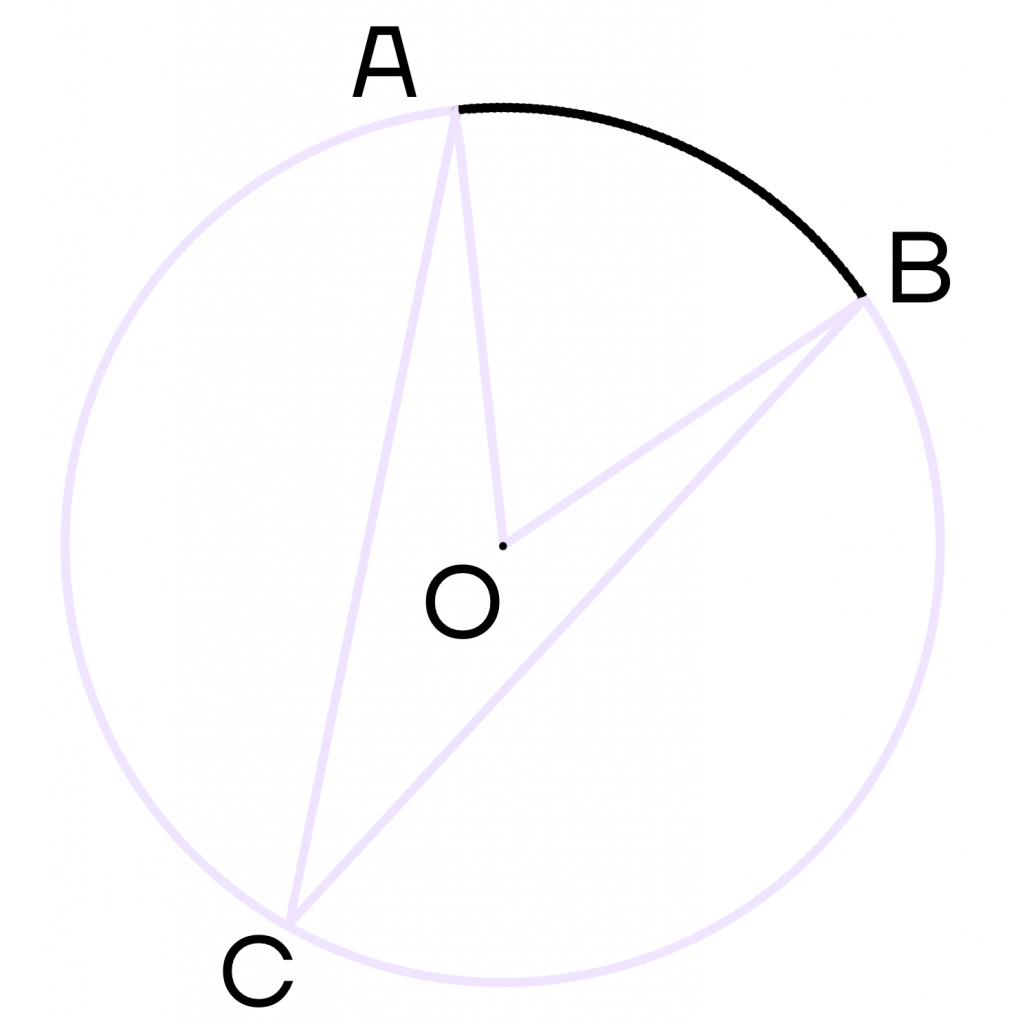
Это легко доказать, если вспомнить, что:
- центральный угол равен градусной мере дуги, на которую он опирается,
- вписанный угол равен половине градусной меры дуги, на которую он опирается.
Следовательно, \(∠ACB = \frac{1}{2}∠AOB\).
Элементы окружности
Радиус – это отрезок, построенный от центра окружности до любой точки на окружности.
Если вспомнить обруч с ленточками, то одна ленточка – это радиус. Радиус обозначается буквой R. В окружности можно построить множество радиусов, и все они будут равны между собой.
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
Можно сразу заметить, что диаметр будет состоять из двух радиусов, которые проведены по разные стороны от центра окружности.
Диаметр обозначается буквой D и равняется двум радиусам.
D = 2R
Хорда – это отрезок, соединяющий две любые точки на окружности. При этом хорда не обязательно проходит через центр окружности.
| Где в ловце снов спрятана хорда?Представим ловец снов. Когда его изготавливают, натягивают нитку от точки на ободе до точки на другом конце обода. Чтобы получился красивый узор, нитки должны быть разной длины и проходить через разные точки – не обязательно через центр. Получается, каждая ниточка внутри ловца слов будет хордой. |
Таким образом, хорда может иметь любой размер и любое направление, главное, чтобы ее начало и конец лежали на окружности.
Рассмотрим свойства хорды.
1 свойство. При пересечении двух хорд произведения их отрезков равны.
Пусть в окружности проведены хорды АВ и CD, которые пересекаются в точке О. Тогда выполняется равенство АО * ОВ = СО * OD.
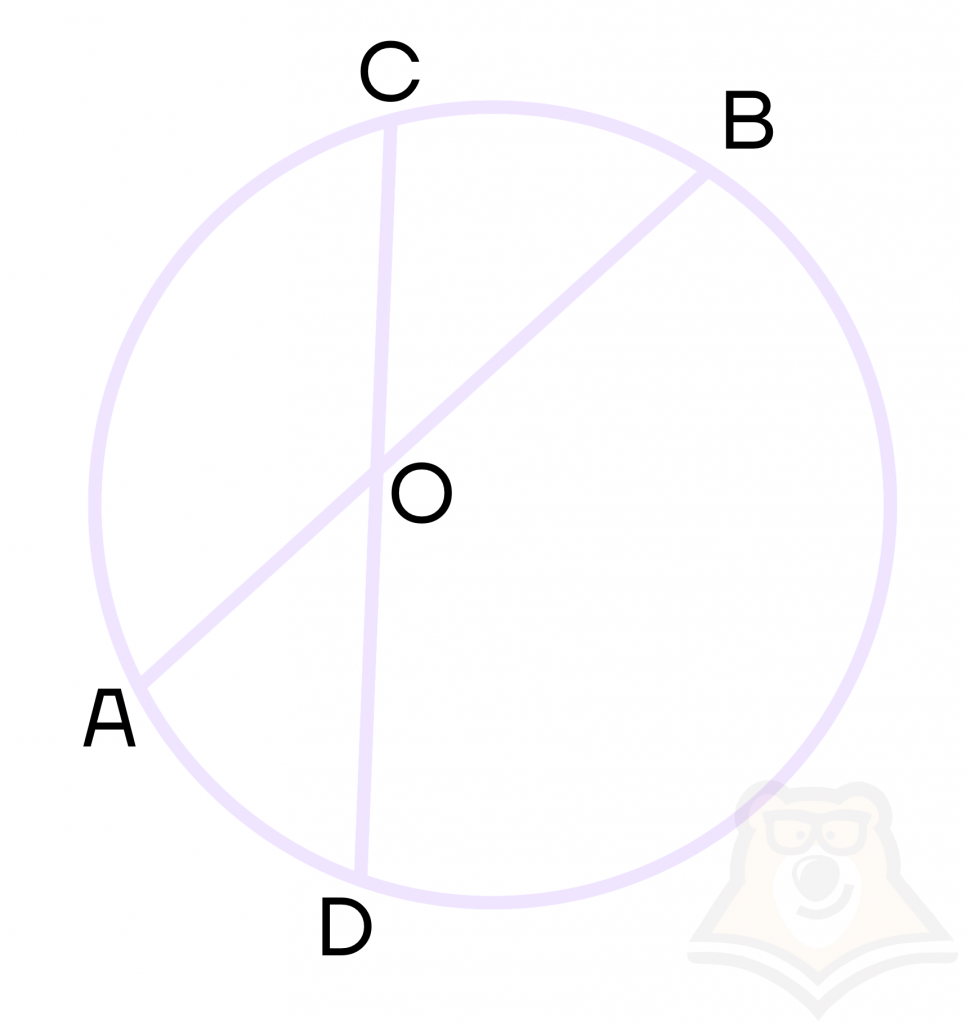
2 свойство. Равные хорды стягивают равные дуги.
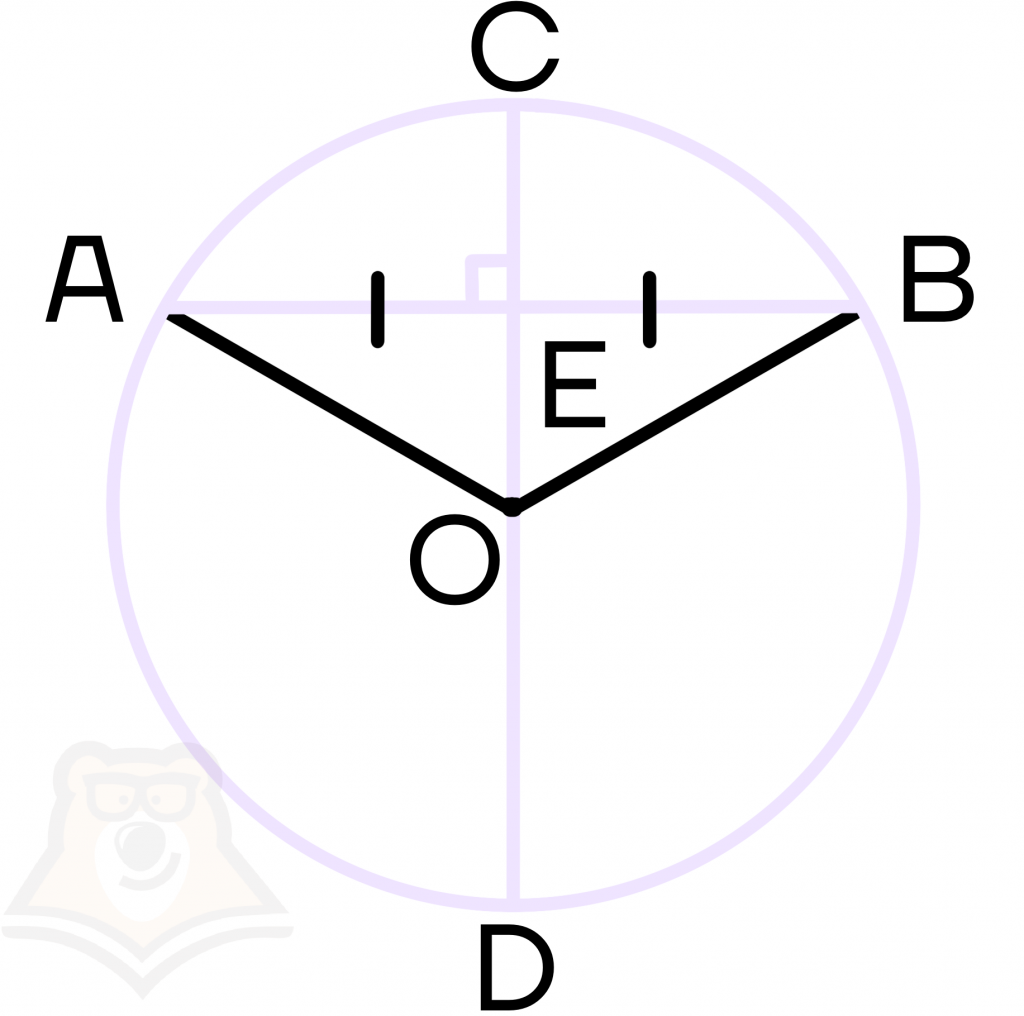
3 свойство. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ей дуги пополам.
Если диаметр CD перпендикулярен хорде АВ, то АЕ = ЕВ.

Рассмотрим, почему выполняется это свойство. Достроим треугольник АОВ, в котором АО и ОВ – радиусы. Радиусы в окружности равны, следовательно, треугольник равнобедренный.
Рассмотрим ОЕ – высота в равнобедренном треугольнике, проведенная к основанию.
Высота в равнобедренном треугольнике, проведенная к основанию, совпадает с медианой и биссектрисой, следовательно, ОЕ – медиана, а значит АЕ = ЕВ.
Свойство 4. Угол между пересекающимися хордами окружности равен половине суммы дуг, заключенных между ними.
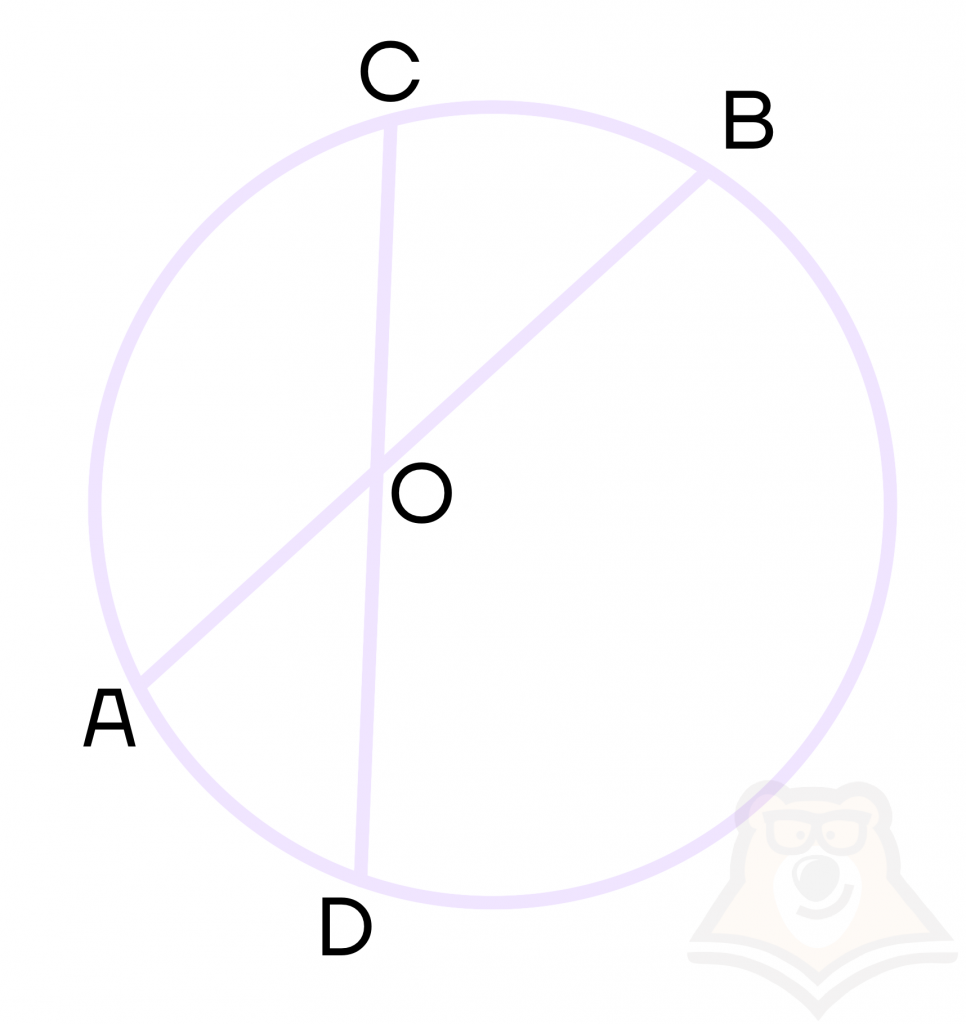
\(∠COB=∠AOD=\frac{1}{2}(\cup BC+ \cup AD)\)
Заметим, что углы COB и AOD равны между собой, поскольку являются .
Дуга – это часть окружности, началом и концом которой являются две произвольные точки.
Допустим, из нашего обруча вырежут какую-то часть. Тогда и вырезанная часть, и оставшаяся часть будут дугами.
Элементы круга
Рассмотрим элементы круга.
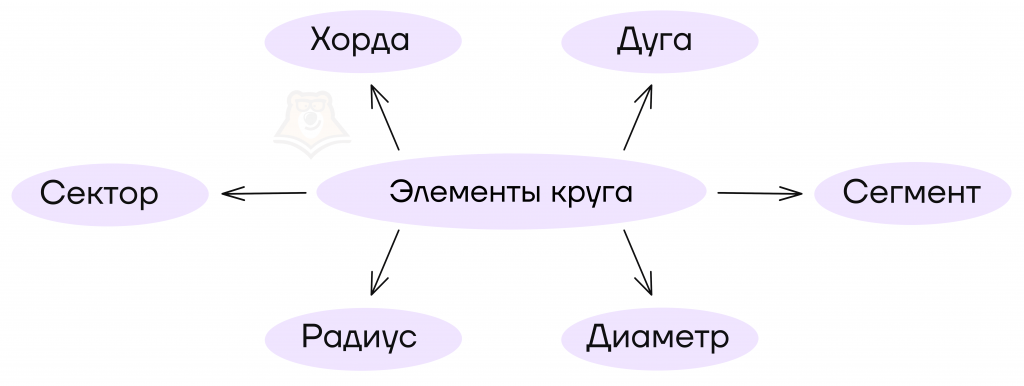
Радиус, диаметр хорды в круге имеют такие же определения, как и в окружности. Поскольку мы теперь рассматриваем не только контур, а всю фигуру, то появляются новые элементы.
Предположим, к нам в гости пришли друзья, и теперь нужно разделить пиццу между всеми. Разумеется, мы разрежем ее на несколько кусочков.

Форма кусочков пиццы очень напоминает сектор круга.
Сектор – это часть круга, которую ограничивают радиусы и дуга.
При этом два радиуса делят круг на два сектора: один больший, а другой меньший. На рисунке один из них закрашен фиолетовым, а другой белым.
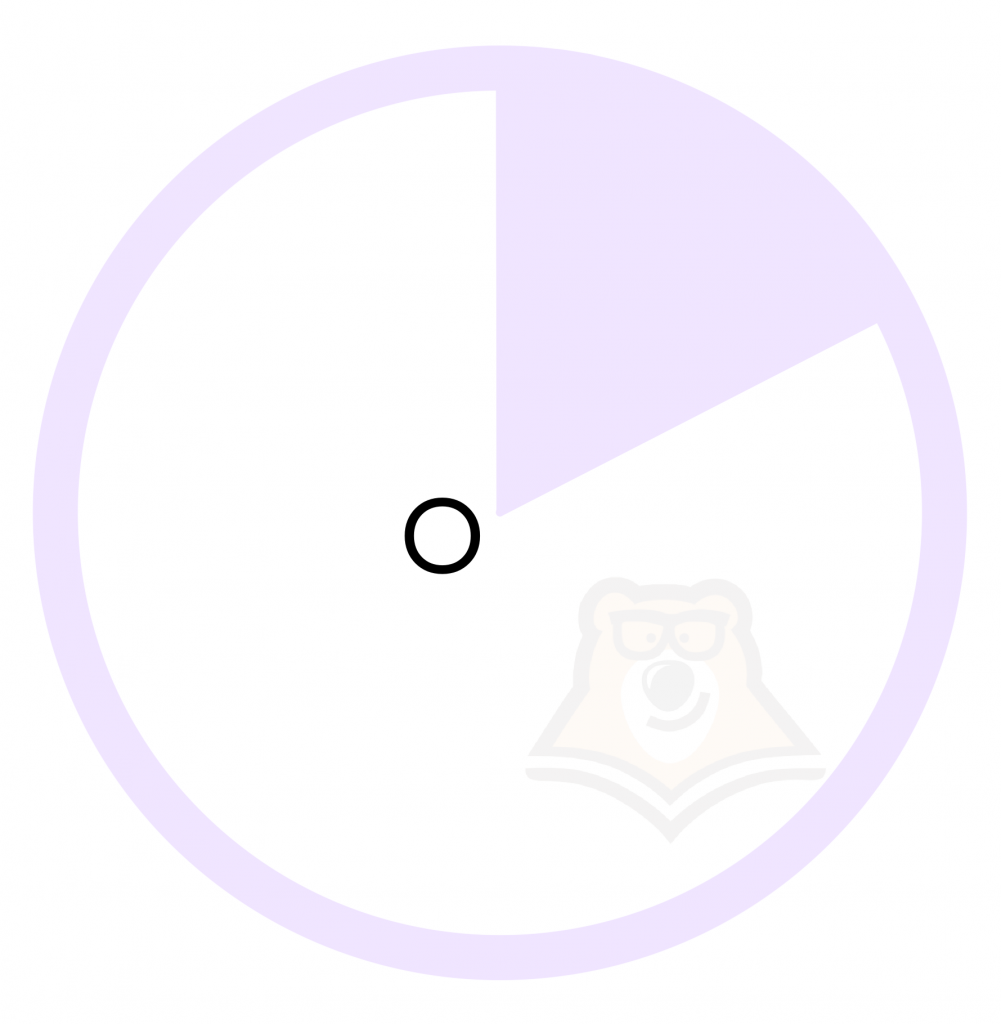
Если мы захотим отрезать только один кусочек пиццы, то и отрезанный кусочек, и оставшаяся пицца будут секторами круга.

Теперь разрежем пиццу иначе. Отрежем кусочек по прямой, не проходя через ее середину:
Таким образом, мы отрежем уже не сектор, а сегмент от пиццы.
Сегмент – это часть круга, которая ограничена хордой и дугой.
Причем одна хорда является границей для двух сегментов: и отрезанный кусочек пиццы, и оставшаяся часть будут сегментами. На рисунке ниже один сегмент закрашен фиолетовым, а другой белым.
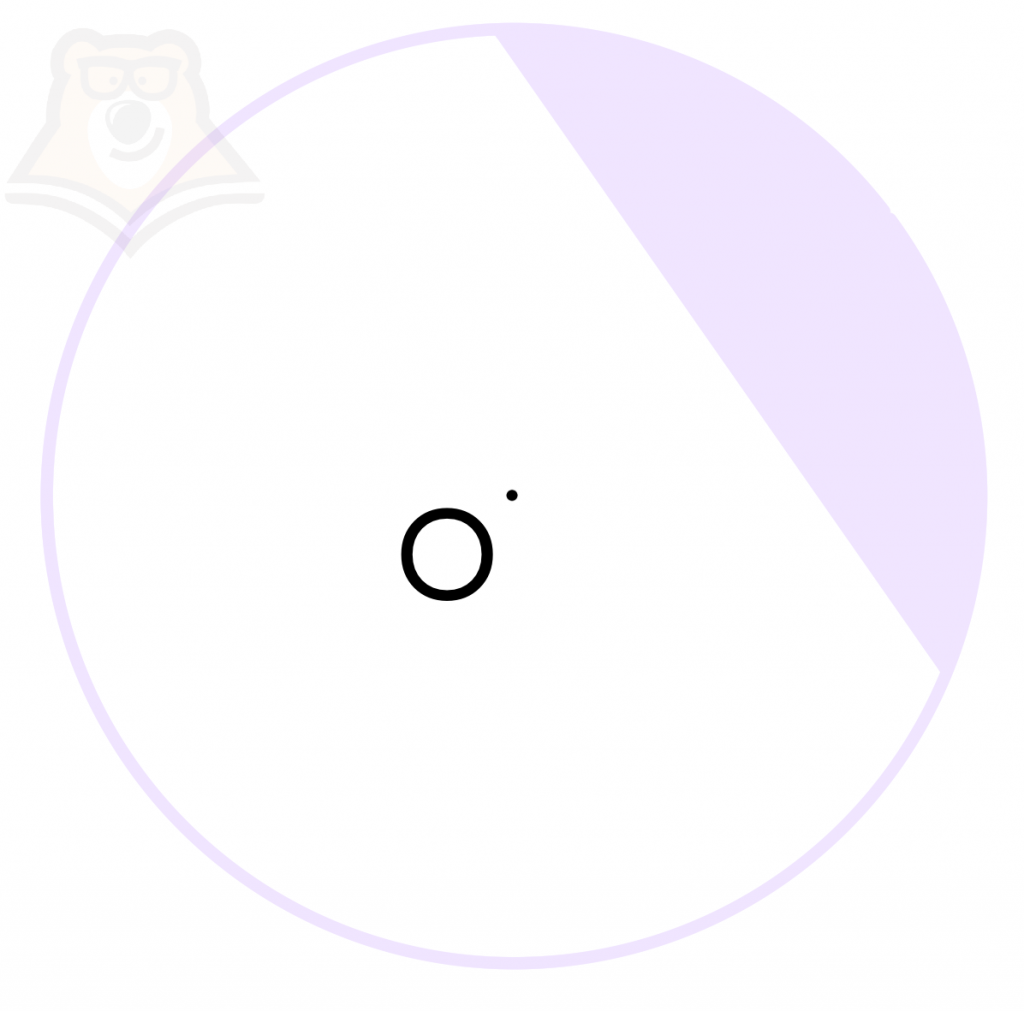
| Подведем итог:И в окружности, и в круге можно встретить радиус, диаметр, хорду и дугу. В круге дополнительно появляются сектор и сегмент. |
Формулы для окружности и круга
Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их.
Однако перед этим необходимо ввести еще несколько терминов.
Длина окружности – это длина кривой, которая образует окружности.
Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности.
Длина дуги – это длина части кривой, которая образует окружность.
Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть.
В таблице ниже приведены основные формулы, которые могут встретиться при решении задач.
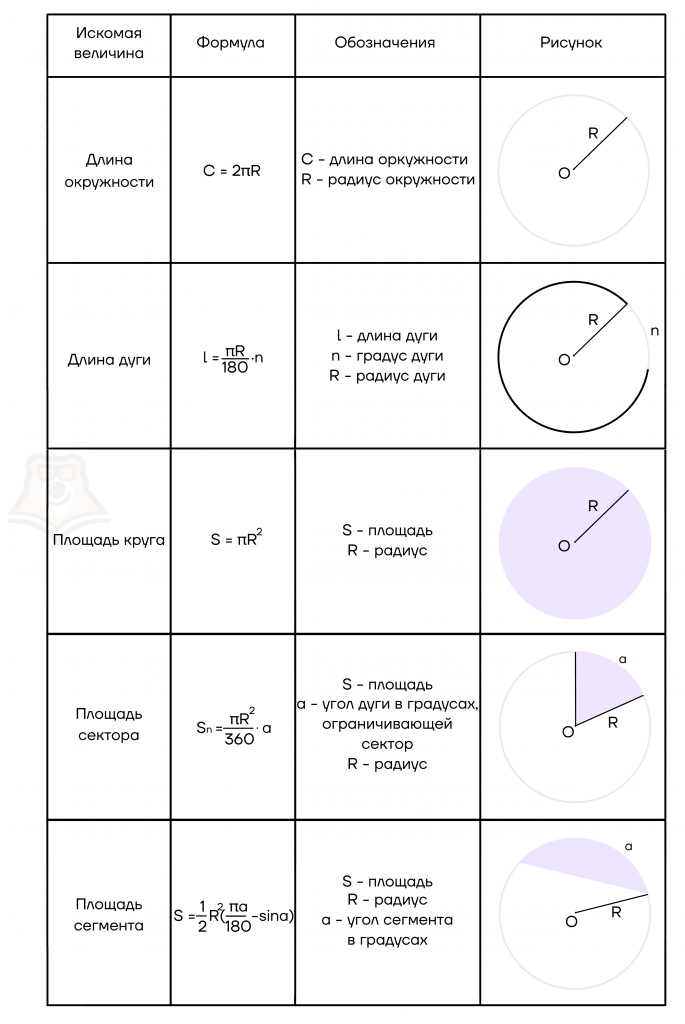
Дуга окружности
Дугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360\(\circ\). Тогда половина дуги окружности будет равняться 180.
При этом дуга, равная 180\(\circ\), называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.
Думаем, хоть раз в жизни вы слышали фразу “повернуться на 180\(\circ\) градусов” или “поменять свое мнение на 180\(\circ\) градусов”. Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180\(\circ\).
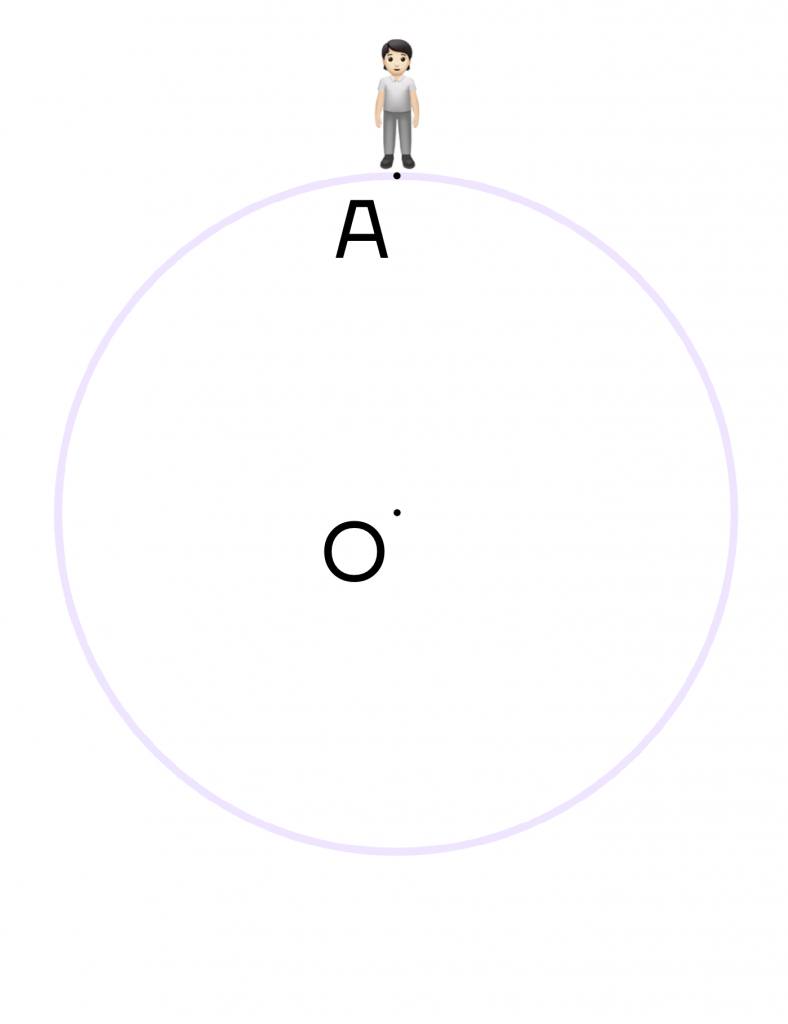
Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности.
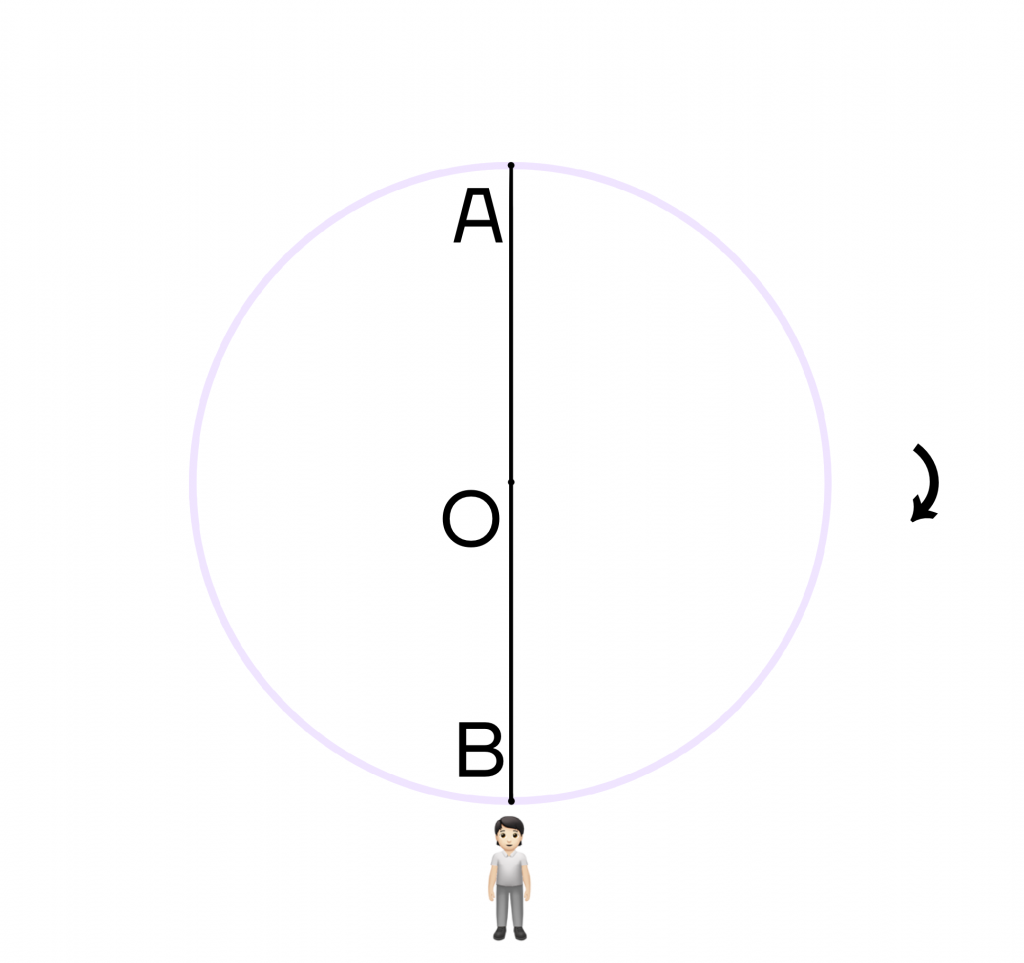
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.
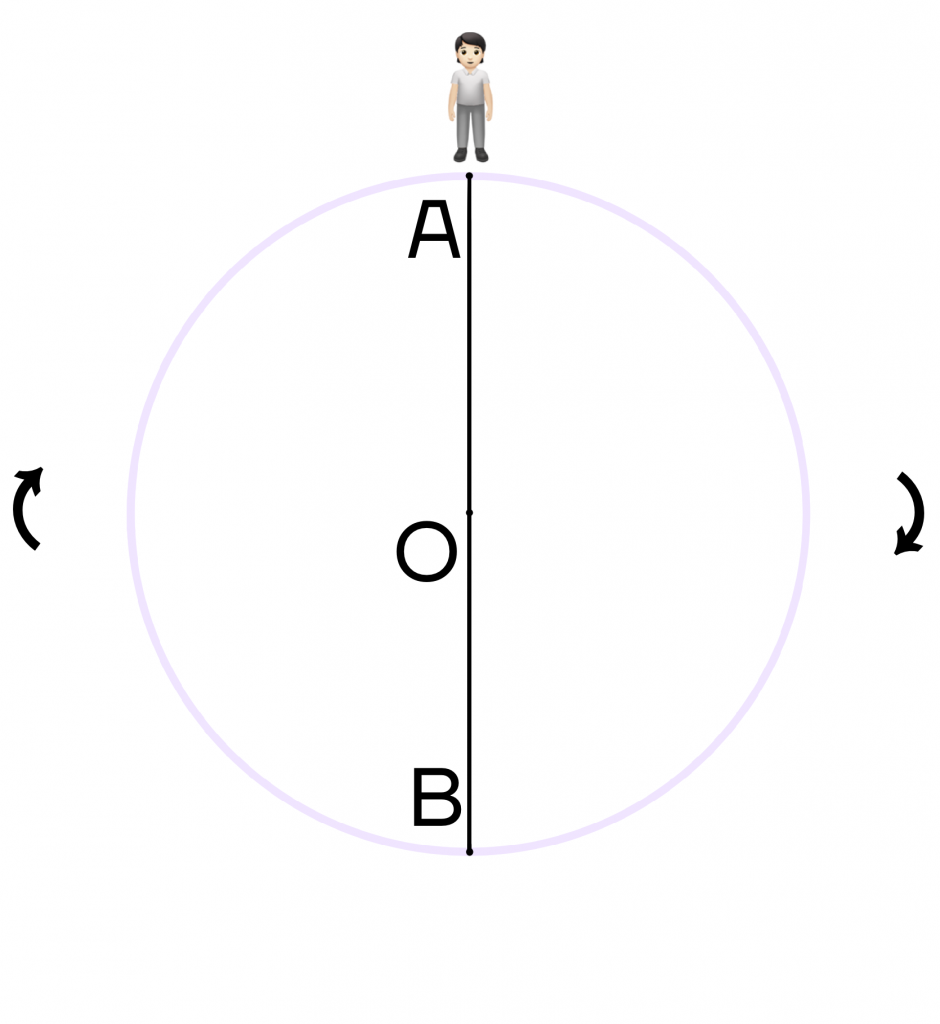
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А.
| Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360? При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально. |
Сумма нескольких слагаемых
Страница 8 — 9
1.Выдели прямоугольником те два числа, сумма которых — круглое число.
Решение:
2. Восстанови по каждому рисунку выражение и найди его значение. Отметь справа галочкой самый удобный способ вычисления.
Решение:
3. Выполни сложение.
Разгадай закономерность, по которой составлены эти суммы. Запиши следующее выражение и вычисли его значение.
Решение: Выпишем первые слагаемые в каждом из примеров: 24, 25, 26, 27, 28 - видим, что каждый последующий элемент, больше предыдущего на единицу, значит следующим в данной последовательности будет число - 29. Далее выпишем вторые слагаемые из примеров: 39, 38, 37, 36, 35 - видим, что каждый последующий элемент, меньше предыдущего на единицу. Значит следующим в данной последовательности будет число 34. Теперь решим примеры и запишем последний пример:
4. Под каждым углом напиши его обозначение. Подчеркни обозначение прямого угла.
Решение:
| Угол ДГУ | Угол АБС | Угол МЕВ |
5. Выполни вычисления. Расшифруй название цветущего кустарника, записав значения выражений в порядке уменьшения.
Решение:
Ответ: название цветущего кустарника — гортензия.
6. Заполни пропуски такими числами, чтобы получились верные записи.
Решение:
7. У Пети, Саши и Коли вместе 80 марок. У Пети столько марок, сколько у Саши и Коли вместе. Сколько марок у Пети?
Можно ли из этого условия узнать, сколько марок у Саши и сколько у Коли?
Решение: Глядя на рисунок можно сделать вывод, что у Пети половина всех марок. Значит: 80 : 2 = 40 (м.) Ответ: у Пети 40 марок. Так как о соотношении марок у Саши и Коли ничего не сказано, то вычислить количество марок у Коли мы не можем.
Страница 10 — 11
8. Восстанови рисунки по выражениям, записанным под ними. Вычисли значения этих выражений удобным способом. Покажи это на рисунке, как сделано в образце.
Решение:
9. Составь выражение для решения каждой задачи и вычисли его значение.
1) В трёх пакетах 60 сушек, во всех поровну. Сколько сушек в одном пакете?
Решение: 60 : 3 = 20 (с.) Ответ: в одном пакете 20 сушек.
2) Вася купил 3 булочки, по 6 р. каждая. Сколько денег он заплатил за всю покупку?
Решение: 6 * 3 = 18 (р.) Ответ: Вася заплатил 18 рублей за 3 булочки.
3) В парке установили 7 деревянных скамеек, а металлических в 2 раза больше. Сколько всего скамеек установили в парке?
Решение: 1) 7 * 2 = 14 (с.) 2) 14 + 7 = 21 (с.) Ответ: в парке установили 21 скамейку.
4) В мешке было 15 кг риса, а в банке — в 5 раз меньше. На сколько больше килограммов риса было в мешке, чем в банке?
Решение: 1) 15 : 5 = 3 (кг) 2) 15 - 3 = 12 (кг) Ответ: в мешке было на 12 кг риса больше, чем в банке.
Страница 10 — 11
10. Отправь в море корабли. Для этого восстанови суммы и разности, записав в окошки нужные цифры, и выполни вычисления.
Решение:
11. За два дня с аэродрома вылетело 96 самолётов. В первый день вылетело на 6 самолётов больше, чем во второй. Сколько самолётов вылетело во второй день?
Решение: 1) 96 - 6 = 90 (с.) 2) 90 : 2 = 45 (с.) 3) 45 + 6 = 51 (с.) Ответ: во второй день вылетел 51 самолёт.
12. Догадайся, как разрезать фигуру голубого цвета по линиям клеток на части, равные жёлтой фигуре. Проведи линии разреза. Сколько таких частей получилось?
Можно ли из этих частей сложить квадрат? Если да, то нарисуй его справа, раскрасив каждую часть своим цветом.
Решение:
Ответ: фигуру голубого цвета можно разрезать на 4 части; из этих 4 частей можно сложить квадрат.
Часть 2:
Страница 4
1
2
3
4
5
6
7
?
Страница 5
1
2
3
4
5
6
7
?
Страница 6
1
2
3
?
Страница 7
1
2
3
4
5
6
7
8
?
Страница 8
1
2
3
4
5
6
7
?
Страница 9
1
2
3
4
5
6
7
8
9
?
Страница 10
1
2
3
4
5
6
7
8
9
?
Страница 11
1
2
3
4
?
Страница 12. Странички для любознательных
1
2
3
4
Страница 13
1
2
3
4
5
6
?
Страница 14
1
2
3
4
5
6
?
Страница 15
1
2
3
4
5
6
7
?
Страница 16
1
2
3
4
5
6
?
Страница 17
1
2
3
4
5
6
?
Страница 18
1
2
3
4
5
6
7
?
Страница 19
1
2
3
4
5
6
7
?
Страница 20
1
2
3
4
5
6
7
8
?
Страница 21
1
2
3
4
5
6
7
8
9
10
Страница 22-23. Странички для любознательных
1
2
3
Страница 24-25. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
Страница 26
1
2
3
4
5
?
Страница 27
1
2
3
4
5
?
Страница 28
1
2
3
4
5
6
7
?
Страница 29
1
2
3
4
5
6
?
Страница 30
1
2
3
4
5
6
?
Страница 31
1
2
3
4
5
6
7
8
Страница 32
1
2
3
4
5
6
7
?
Страница 33-35. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Страница 38-39. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
10
11
Вариант 2
1
2
3
4
5
6
7
8
9
10
11
Страница 40. Странички для любознательных
1
2
Страница 42
1
2
3
4
5
6
7
8
?
Страница 43
1
2
3
4
5
6
7
?
Страница 44
1
2
3
4
Страница 45
5
6
7
8
9
10
11
12
?
Страница 46
1
2
3
4
5
6
7
8
9
10
?
Страница 47
1
2
3
4
5
6
7
?
Страница 48
1
2
3
4
5
6
?
Страница 49
1
2
3
4
5
6
7
8
?
Страница 50
1
2
3
4
5
6
?
Страница 51
1
2
3
4
5
6
7
8
9
Страница 52-53. Странички для любознательных
1
2
3
4
5
6
7
8
Страница 54
1
2
3
4
5
?
Страница 55. Задачи — Расчеты
1
2
3
4
Страница 56-57. Странички для любознательных
1
2
3
4
Страница 58-61. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Страница 62-63. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
Вариант 1
1
2
3
4
5
6
7
8
9
Страница 64. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
Страница 66
1
2
3
4
5
6
7
?
Страница 67
1
2
3
4
5
6
7
8
?
Страница 68
1
2
3
4
5
?
Страница 69
1
2
3
4
5
6
7
?
Страница 70
1
2
3
4
5
6
7
8
9
?
Страница 71
1
2
3
4
5
6
?
Страница 72
1
2
3
4
5
6
7
?
Страница 73
1
2
3
4
Страница 74
1
2
3
4
5
6
?
Страница 75. Странички для любознательных
1
2
3
4
5
Страница 76-79. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Страница 80. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
Страница 82
1
2
3
4
5
6
7
?
Страница 83
1
2
3
4
5
6
7
?
Страница 84
1
2
3
4
5
6
7
8
?
Страница 85
1
2
3
4
5
?
Страница 86
1
2
3
4
?
Страница 87. Странички для любознательных
1
2
3
Страница 88
1
2
3
4
5
?
Страница 89
1
2
3
4
5
6
?
Страница 90
1
2
3
4
5
6
7
8
?
Страница 91
1
2
3
4
5
6
?
Страница 92
1
2
3
4
5
6
7
?
Страница 93
1
2
3
Страница 94
4
5
6
?
Страница 95
1
2
3
4
5
6
7
?
Страница 96
1
2
3
4
5
6
7
8
Страница 98
1
2
3
4
5
6
?
Страница 99-102. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Что узнали, чему научились в 3 классе?Страница 103. Нумерация
1
2
3
4
5
6
7
8
Страница 103-104. Сложение и вычитание
1
2
3
4
5
6
7
8
Страница 105-106. Умножение и деление
1
2
3
4
5
6
7
8
Страница 107. Правила о порядке выполнения действий
1
Страница 107-108. Задачи
1
2
3
4
5
6
7
8
9
10
11
Страница 109. Геометрические фигуры и величины
1
2
3
4
5
Тексты для итоговой контрольной работыСтраница 110. Задания базового уровня
1
2
3
4
5
6
7
Страница 111. Задания повышенного уровня
1
2
3
4
5
6
7































