Задачи на умножение-деление в предалах 100.
1. Ученики 1 класса по заданию учительницы взяли в библиотеке по 2 сказки Пушкина. Сколько всего сказок Пушкина выдал библиотекарь второклассникам, если известно, что во втором классе учится 20 человек?
2. Концертный зал имеет 11 рядов, в каждом ряду по 12 кресел. Сколько зрительских мест в этом зале?
3. Чтобы полить одну грядку с огурцами, бабушке нужно 3 л воды. Сколько литров воды потребуется бабушке, чтобы полить 6 таких грядок?
4. В первой банке 12 литров сока. Во второй — в 2 раза меньше. Сколько сока надо перелить из первой банки во вторую, чтобы в обеих банках стало сока поровну?
5. У белки в дупле заготовлены на зиму грибы и орехи. Грибов белка заготовила 86 штук, а орехов всего 4 штуки. Во сколько раз больше белка заготовила грибов, чем орехов?
6. Расстояние от глаз телезрителя до экрана телевизора должна быть в 4 раза больше, чем диагональ экрана. каким должно быть это расстояние, если диагональ экрана равна 36 см?
7. Акула за 10 минут проплывает 1 000 м. Какое расстояние она проплывает за 1 минуту?
8. Заяц за час может пробежать 60 км, а волк на 15 км меньше. какое расстояние может пробежать волк за 1 час?
9. Миша каждый день решал по 5 математических задач. Сколько задач Миша решил за неделю?
10. В магазине в понедельник продали 26 сказок Пушкина, а во вторник в 2 раза меньше. Сколько сказок было всего продано за 2 дня?
Уважаемые читатели!
Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.
Материалы в архиве не помечены водяными знаками!
Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.
Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо!!!
Порядок выполнения арифметических действий в выражениях со скобками
Рассмотри выражения и объясни почему действия следует выполнять в порядке указанном синими цифрами
Нажмите Ctrl+D , чтобы добавить сайт в избранное.
ГДЗ к странице 33
1. Рассмотри выражения в каждой рамке. Объясни порядок выполнения действий, указанный синими цифрами.Выполни вычисления. Сравни значения выражений.
1) 32 − 7 = 252) 100 : 25 = 43) 88 : 2 = 444) 4 + 44 = 48
1) 15 + 9 = 242) 6 * 5 = 303) 30 − 28 = 24) 24 * 2 = 48
27 * 3 − (12 + 56 : 4) − 28 : 4 = 48
1) 56 : 4 = 142) 12 + 14 = 263) 27 * 3 = 814) 28 : 4 = 75) 81 − 26 = 556) 55 − 7 = 48
2. Укажи порядок выполнения действий и вычисли значения выражений.Сравни выражения и их значения. Сделай вывод.
2 3 196 : 6 * (2 + 4)=96
2 1 396 : (6 * 2) + 4=12
Ответы разные, значит порядок действий имеет большое значение.
3. Садоводам надо было посадить 230 кустов смородины и 150 кустов крыжовника. В первый день они посадили 8 рядов смородины, по 20 кустов в каждом ряду, и 4 ряда крыжовника, по 30 кустов в каждом ряду.Объясни, что означают выражения.
4. Начерти в тетради отрезки AC и BD, как показано на рисунке. Восстанови четырехугольник ABCD по его диагоналям AC и BD.Выполни измерения и вычисли периметр этого четырехугольника в сантиметрах. Что можно сказать о длинах сторон этого четырехугольника?Является ли он квадратом? (Нет) Почему? (Углы не прямые) Можно ли изменить чертеж, чтобы четырехугольник ABCD стал квадратом? (Да) Объясни свой ответ.
Порядок вычисления простых выражений
Определение 1
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Пример 1
Условие: вычислите, сколько будет 7−3+6.
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7−3+6=4+6=10
Ответ: 7−3+6=10.
Пример 2
Условие: в каком порядке нужно выполнять вычисления в выражении 62·83?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Пример 3
Условие: подсчитайте, сколько будет 17−5·63−2+42.
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30, потом 30 разделить на 3 и получить 10. После этого делим 4 на 2, это 2. Подставим найденные значения в исходное выражение:
17−5·63−2+42=17−10−2+2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17−10−2+2=7−2+2=5+2=7
Ответ: 17−5·63−2+42=7.
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6.
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3, получаем 4, после чего к полученной разности 4 прибавляем 6, получаем 10.
Кратко решение можно записать так: 7−3+6=4+6=10.
Ответ:
7−3+6=10.
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3.
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
сначала 6 делим на 2, это частное умножаем на 8, наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2.
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6, получаем 30, это число делим на 3, получаем 10. Теперь 4 делим на 2, получаем 2. Подставляем в исходное выражение вместо 5·6:3 найденное значение 10, а вместо 4:2 — значение 2, имеем 17−5·6:3−2+4:2=17−10−2+2.
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7.
Ответ:
17−5·6:3−2+4:2=7.
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Ответы к стр. 6
11. Рассмотри выражения и объясни, почему действия следует выполнять в порядке, указанном синими цифрами.
2 1 3 3 2 1 320 (60 — 52) • 6 = 240 230 + (170 + 40 2) = 420
1 3 2 2 1 3 (820 + 80) — (310 — 60) = 650 (420 + 16 • 5) 100 = 5
Сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание; затем выполняются остающиеся действия, причём опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
12. В каждом выражении сначала укажи порядок выполнения действий, а потом вычисли его значение.
3 2 1 2 3 1 470 — (500 — 25 • 3) = 45 (120 — 80) (100 25) = 10
2 1 3 3 2 1 (300 + 160 4) 2 = 170 100 — 32 • (87 — 84) = 4
3 1 2 2 1 3 500 + (400 — 160 + 40) = 780 280 — 140 • 2 + 7 = 7
2 1 3 1 3 2 (870 — 240 • 3) 5 = 30 (81 3) (9 • 3) = 1
13. У Нины было 50 р. и ещё 8 монет, по 5 р. каждая. Сколько всего денег было у Нины?
1) 5 • 8 = 40 (р.) — всего монет 2) 50 + 40 = 90 (р.) О т в е т: всего у Нины было 90 рублей.
14. В 2 одинаковых спальных вагонах поезда 120 мест. Сколько мест в 7 таких вагонах? в 10 таких вагонах?
1) 120 2 = 60 (м.) — в одном спальном вагоне 2) 60 • 7 = 420 (м.) — в 7 вагонах 3) 60 • 10 = 600 (м.) — в 10 вагонах О т в е т: 420 мест; 600 мест.
Задачи на умножение и деление 2 класс в два действия
КАРТОЧКА 1
Прочитай задачи. Запиши решение и ответ.
- В магазине продаются 5 наборов кастрюль по 3 штуки в наборе и ещё 9 кастрюль отдельно. Сколько всего кастрюль продаётся в магазине?
- Антон поймал 16 окуней, а щук в 2 раза меньше. Сколько всего рыб поймал Антон?
- Идёт колонна солдат: 9 рядов по 2 солдата и 3 солдата впереди. Сколько солдат идёт в колонне?
КАРТОЧКА 2
Прочитай задачи. Запиши решение и ответ.
- Борис отжимается от пола 27 раз, а Руслан в 3 раза меньше. На сколько меньше отжиманий делает Руслан?
- Один класс выучил 7 песен, это в 2 раза меньше, чем второй. Сколько всего песен выучили два класса?
- Оксана сложила из спичек один шестиугольник и 8 одинаковых треугольников. Сколько спичек использовала Оксана?
КАРТОЧКА 3
Прочитай задачи. Запиши решение и ответ.
- 12 красных и 6 жёлтых яблок разложили поровну на 2 тарелки. Сколько яблок лежит на каждой тарелке?
- Школьники посадили 2 ряда яблонь по 8 деревьев и 17 грушевых деревьев. Сколько всего деревьев посадили школьники?
- На трёх ветках сидело по 6 воробьёв. Прилетело ещё 13 воробьёв. Сколько стало птиц?
КАРТОЧКА 4
Прочитай задачи. Запиши решение и ответ.
- 3 ящика с бананами весят 30 кг, а ящик с хурмой 4 кг. На сколько легче ящик с хурмой?
- Глубина колодца 50 метров, а глубина оврага на 40 метров меньше. Во сколько раз глубина оврага меньше, чем глубина колодца?
- Когда портниха пришила по 5 пуговиц к 3 пальто, у неё осталось 37 пуговиц. Сколько пуговиц было у портнихи?
КАРТОЧКА 5
Прочитай задачи. Запиши решение и ответ.
- На двух этажах 14 окон. Сколько окон на трёх этажах?
- В двух вёдрах 20 литров молока. Сколько молока в 8 таких же вёдрах?
- Почтальон разнёс 8 журналов, а газет в 3 раза больше. Сколько газет и журналов разнёс почтальон?
КАРТОЧКА 6
Прочитай задачи. Запиши решение и ответ.
- Таня купила 4 ручки по 3 рубля и тетрадь по 19 рублей. Сколько денег она заплатила?
- С одной грядки собрали 17кг клубники, а с другой 13кг. Клубнику разложили в корзины по 3 кг в каждом. Сколько получилось корзин?
- Настя собрала 38 орехов, а Петя — 42 ореха. Все орехи рассыпали в пакеты по 10 орехов в каждый. Сколько понадобилось пакетов?
КАРТОЧКА 7
Прочитай задачи. Запиши решение и ответ.
- Для приготовления раствора строители взяли 7 кг цемента, а песка в 3 раза больше. Сколько строительного материала было приготовлено?
- 20 яиц идёт на приготовление 10 порций омлета. Сколько яиц нужно для приготовления 5 порций?
- У Саши 15 жёлтых шаров. Это в 3 раза больше, чем красных. На сколько меньше красных шаров у Саши?
КАРТОЧКА 8
Прочитай задачи. Запиши решение и ответ.
- Катя нарисовала 14 картин, а её подруга в 2 раза меньше. На сколько больше картин нарисовала Катя?
- В зале 5 колонн украсили 50 шариками. Сколько нужно шариков, чтобы украсить 8 колонн?
- В 10 коробках — 60 карандашей. Сколько надо взять коробок, чтобы разместить 12 таких же карандашей?
КАРТОЧКА 9
Прочитай задачи. Запиши решение и ответ.
- В трёх вазах лежало по 9 яблок. 8 яблок съели. Сколько яблок осталось?
- Когда в кафе сидело 9 посетителей, свободных мест оставалось в 3 раза больше, сколько посетителей может принять кафе?
- Одна курочка снесла 6 яиц, это в 3 раза меньше, чем другая. Сколько яиц они снесли вместе?
КАРТОЧКА 10
Прочитай задачи. Запиши решение и ответ.
- Для уроков труда купили 4 набора цветной бумаги по10 листов в каждом наборе. На поделки истратили 18 листов. Сколько листов осталось?
- Свете 18 лет, а Юля в 2 раза моложе. На сколько лет Юля младше Светы?
- 3 утки вывели по 9 утят, а гусыня — 8. На сколько меньше родилось гусят, чем утят?
КАРТОЧКА 11
Прочитай задачи. Запиши решение и ответ.
- Соловей летел 3 дня по 10 км и ещё день 14 км. Какой путь пролетел соловей?
- У Алёши 63 сказки. В трёх книгах по 8 сказок, остальные на дисках. Сколько сказок на дисках?
- Дети смастерили 54 игрушки. 10 мальчиков сделали по 2 игрушки. Сколько игрушек изготовили девочки?
Числа от 1 до 100 Умножение и делениеПорядок выполнения действийОтветы к стр. 27
1. Вспомни, в каком порядке надо выполнять действия (с. 24). Определи порядок выполнения действий в следующих выражениях и вычисли их значения.
18 : (11 — 5) + 47 2 • 9 — 6 • 3 24 : 3 + 9 – 3
2 1 3
18 (11 — 5) + 47 = 18 6 + 47 = 3 + 47 = 50 1 3 2
2 • 9 — 6 • 3 = 18 — 6 • 3 = 18 — 18 = 0 2 1 3
24 3 + 9 — 3 = 8 + 9 — 3 = 17 — 3 = 14
2. Составь выражения по схемам; определи в них порядок действий и вычисли их значения.
[] — [] + [] [] — [] : [] [] — ([] + []) : []
[] : [] • [] [] + [] • [] [] + [] • ([] — [])
[] — [] • [] [] + [] : [] [] • ([] + []) + []
72 — 53 + 12 = 19 + 12 = 31
21 3 • 5 = 7 • 5 = 35
56 — 12 • 3 = 56 — 36 = 20
43 — 18 3 = 43 — 6 = 2735 + 13 • 4 = 35 + 52 = 87
63 + 24 8 = 63 + 3 = 66
95 — (44 + 76) 4 = 95 — 120 4 = 95 — 30 = 65
81 + 2 • (46 — 34) = 81 + 2 • 12 = 81 + 24 = 105
14 • (2 + 3) + 18 = 14 • 5 + 18 = 70 + 18 = 88
3. Составь по таблице три задачи и реши их.
| Расход ткани на один костюм | Количество костюмов | Расход ткани на все костюмы |
| 3 м | 2 шт. | ? |
| ? | 2 шт. | 6 м |
| 3 м | ? | 6 м |
1) На изготовление одного костюма расходуется 3 м ткани. Сколько метров ткани потребуется для изготовления двух таких костюмов?
3 • 2 = 6 (м) — ткани на два костюма
О т в е т: на два костюма потребуется 6 м ткани.
2) На изготовление двух одинаковых костюмов потратили 6 м ткани. Сколько метров ткани пошло на один костюм?
6 2 = 3 (м) — ткани на один костюм
О т в е т: на один костюм пошло 3 м ткани.
3) На изготовление одного костюма требуется 3 м ткани. Сколько таких костюмов можно изготовить из 6 м ткани?
6 2 = 3 (шт.) — костюмов
О т в е т: можно изготовить 3 костюма.
4.Сшили 4 плаща, расходуя на каждый по 3 м ткани. Поставь вопрос и реши задачу. Составь и реши две задачи, обратные данной.
Сколько всего метров ткани потратили на изготовление плащей?
3 • 4 = 12 (м) — ткани потратили всего
О т в е т: всего потратили 12 м ткани.
1) Из 12 м ткани изготовили 4 одинаковых плаща. Сколько метров ткани пошло на один плащ?
12 4 = 3 (м) — ткани пошло на один плащ
О т в е т: на один плащ пошло 3 м ткани.
2) На изготовление одного плаща требуется 3 м ткани. Сколько таких плащей можно изготовить из 12 м ткани?
12 3 = 4 (шт.) — плащей
О т в е т: можно изготовить 4 плаща.
5. Какая фигура лишняя? Найди разные решения.

1) Лишняя фигура 2 — треугольник, так как все остальные фигуры четырёхугольники.
2) Лишняя фигура 5 — закрашенный четырёхугольник, так как все остальные фигуры не закрашены.
3) Лишняя фигура 1 — параллелограмм, так как у всех остальных фигур есть хотя бы один прямой угол.
7 • 3 — (16 + 4) 12 : (3 • 2) — 2 18 : 9 + 27 : 3
7 • 3 — (16 + 4) = 7 • 3 — 20 = 21 — 20 = 1
12 (3 • 2) — 2 = 12 6 — 2 = 2 — 2 = 0
18 9 + 27 3 = 2 + 27 3 = 2 + 9 = 11
Задание на полях
К 1 прибавили 5 — получили 6, к 6 прибавили 6 (5 + 1) — получили 12, к 12 прибавили 7 (6 + 1) и так далее, то есть каждый раз прибавляется число на 1 больше того, которое прибавили. Следующие числа 36 + 10 = 46 и 46 + 11 = 57.
| ← Предыдущая | Следующая → |
Математика 2 класс. Разрезные карточки
В настоящем пособии предложен дидактический материал по математике для 2 класса. Задания-карточки предназначены для организации самостоятельной дифференцированной работы обучающихся и содержат разнообразный материал, который может быть использован на различных этапах изучения темы. Данное пособие окажет помощь учителю в подборе дополнительных заданий как для усвоения, так и закрепления программного материала. Пособие адресовано учителям начальной школы, может быть полезно студентам педагогических заведений, а также родителям.
Подробное описание Введение Дидактический материал по математике для 2 класса (1–4) окажет помощь в подборе дополнительных заданий для усвоения программного материала, закрепления по всем темам Основными целями данного пособия являются: – помощь в достижении и овладении обязательным уровнем усвоения программы по математике за 2 класс; – развитие у детей интереса к математике; – формирование стремления к решению все более сложных задач и упражнений; – приобретение новых вычислительных навыков и их совершенствование; – воспитание самостоятельности в принятии и поиске вариантов решения. Материал включает в себя задания по основным разделам и темам курса, указанным на протяжении всего пособия. Например: I Раздел: Числа от 1 до 100. Нумерация. Тема № 1: Числа от 1 до 20. Тема № 2: Счет десятками. Образование и запись чисел от 20 до 100. Тема № 3: Поместное значение цифр. И так далее. В каждой теме предлагается по 3 карты. В целях обеспечения дифференциации обучения и самостоятельности детей карта дана в трех вариантах. В-1. – Ориентирован на минимальный уровень требований и предлагается слабо- и среднеуспевающим детям. В-2. – Рассчитан на учащихся с хорошим уровнем математических знаний и умений. В-3. – Предлагается «сильным» ученикам, так как имеет задания повышенной трудности. Надо отметить, что к концу учебного года во всех вариантах прослеживается усложнение предлагаемых заданий. Данными карточками могут пользоваться учителя, работающие в классах как традиционного, так и развивающего обучения. Содержание Раздел I. Числа от 1 до 100. Нумерация 4 Тема: Числа от 1 до 20 4 Тема: Счет десятками. Образование и запись чисел от 20 до 100 8 Тема: Поместное значение цифр 13 Тема: Однозначные и двузначные числа 18 Тема: Миллиметр. Закрепление 22 Тема: Число 100 28 Тема: Метр. Таблица единиц длины 31 Тема: Сложение и вычитание вида 35 + 5, 35 – 30, 35– 5. 36 Тема: Замена двузначного числа суммой разрядных слагаемых (36 = 30 + 6). 40 Тема: Рубль, копейка. Закрепление 44 Раздел II. Сложение и вычитание 48 Тема: Задачи, обратные данной. Сумма и разность отрезков. 48 Тема: Задачи на нахождение неизвестного уменьшаемого и вычитаемого. 53 Тема: Час, минута. Определение времени по часам. Закрепление 58 Тема: Длина ломаной. Закрепление 62 Тема: Порядок действий. Скобки 67 Тема: Числовое выражение 71 Тема: Сравнение числовых выражений 75 Тема: Периметр многоугольника 81 Тема: Свойства сложения 84 Тема: Упражнения для закрепления 87 Раздел III. Числа от 1 до 100. Умножение и деление 91 Тема: Конкретный смысл действия умножения 91 Тема: Прием умножения с помощью сложения 96 Тема: Задачи на нахождение произведения 100 Тема: Периметр прямоугольника 104 Тема: Приемы умножения единицы и нуля 108 Тема: Названия компонентов и результата умножения 112 Тема: Переместительное свойство умножения 117 Тема: Конкретный смысл действия деления (с помощью решения задач на деление по содержанию) 122 Тема: Конкретный смысл действия деления (с помощью решения задач на деление на равные части) 127 Тема: Названия компонентов и результата деления 131 Тема: Связь между компонентами и результатом умножения 135 Тема: Прием деления, основанный на связи между компонентами и результатом умножения 139 Тема: Приемы умножения и деления на 10 144 Тема: Задачи с величинами: цена, количество, стоимость 148 Тема: Табличное умножение и деление. Умножение числа 2 и на 2. Приемы умножения числа 2 151 Тема: Деление на 2. Закрепление 155 Тема: Умножение числа 3 и на 3 159 Тема: Деление на 3. Закрепление 163 Тема: Повторение пройденного материала за год 167 Литература 172
Авторы: Стромчинская Е. М. Код: 320е Страниц: 175 ISBN: 978-5-7057-1774-3 Серия: Дидактический материал Вес: 131г
Предварительный просмотр:
1) 1000 — (310 — 9 + 587 + 8 — 94 + 189) — 4
2) 782 — (2 + 72 + 2) — (13 — 7) — 686 — 8
3) 47 + 284 — 17 — (66 + 188) — (1000 — 956 + 9)
4) (65 + 145) + 99 — (41 — 32) — (360 — 67 — 1)
5) 193 + 7 — 193 — (335 + 349 — 93 — 579 — 9)
6) 23 + 1 + 483 — 19 — (904 + 96 — 991) — 474
7) 845 — 38 — (18 — 3 — ![]() — (819 — 21) + 4
— (819 — 21) + 4
![]() 811 — (70 — 6) — 6 — 651 — (1000 — 951 + 34)
811 — (70 — 6) — 6 — 651 — (1000 — 951 + 34)
9) 804 — (560 — 556) — (726 — 3) — (134 + 2 — 67)
10) 519 + 3 — (906 — 6 — 890 — 2 + 506 + 1) — 3
11) 35 + 6 + 51 + 346 — 4 — (1 + 914 + 85 — 571)
12) 701 — 1 — (129 — 57 — 5 + 625) — (42 — 6 — 34)
13) 1000 — (849 — 693 — 154 + 4 + 67 — 3) — (925 — 2)
14) 69 + (893 — 884) + 426 + (200 — 195) — 49 — (8 + 444)
15) 98 + 151 — 7 + 58 — (25 — 18 + 842 — 4 — 549)
16) 998 + 2 — (899 + 89 — 2) + 51 + 189 + 5 — 254
17) 506 — 6 — (808 — 376 + 59) — (432 + 7 — 438 + 2)
18) 1000 — (969 — 1) — (797 — 6 — 698 — 19 + 2 — 51)
19) 118 — (802 — 2 — 763) — 7 — (75 — 3) + (14 — ![]()
20) 623 — 23 — (593 — 9 — 85 + 2) — 98 + 3
21) 14 — (902 + 98 — 991) + 924 — 8 — 825 — 91
22) 914 + 36 — 348 — (8 — 6) — (59 + 488 + 47)
23) 1000 — (4 + 924 — 6) — (703 — 6 — 642 + 16)
24) (400 — 326) + 441 — (81 — ![]() + 4 — (436 + 2)
+ 4 — (436 + 2)
25) 669 — 69 — (42 + 520 — 5 + 36) — 3
26) 876 — (1000 — 910 + 1) — 2 + 79 — 857
27) 450 — (2 + 6) — (908 — 8 — 388 — 76)
28) 1000 — (32 + 881 — 4) — (109 — 21) + 4
29) (34 — 23) + (12 + 252) — 75 — (84 + 108)
30) 853 + 3 — (73 + 18 — 1 — 34) — 796
31) 997 + 3 — (3 + 941 — 45) — 9 — 87
32) 174 — (65 — 15 — 42) + 34 — (132 + 62)
33) 72 + 6 — (136 — 73) — (1000 — 987 — 5)
34) (46 + 868) — (16 — 2) — (837 — 17) — 72
35) 378 + 4 — (196 + 43 — 156 — 1) — 296
36) 991 + 9 — (60 — 56 — 3 + 988 + 6)
37) 38 + 491 — (10 — 8 + 27) — (503 — 9)
38) 1000 — (541 + 429) — (729 — 61 — 9 — 636)
39) (14 — 9) + (268 + ![]() — 81 — (239 — 47)
— 81 — (239 — 47)
40) 660 + 14 — 595 — (694 — 94 — 529 + 4)
41) 1000 — (78 + 1 + 473 — 74 + 516) — 1
42) 94 — (937 — 933) — (91 + 357 — 48 — 316)
43) 1000 — (938 — 4) — 8 — (5 + 40 + 6)
44) (811 — 57) — (40 + ![]() — 6 — (620 + 72)
— 6 — (620 + 72)
45) 787 + 7 — (57 — 8 + 45) — 699 + 3
46) 710 — (996 + 4 — 997 + 38 — 5) — 669
47) 416 + 5 — (31 — 1 — 9) — (467 — 73)
48) 1000 — (68 + 912) — (847 + 4 — 846 + ![]()
49) (600 — 428) — (63 — 4) — 2 — (102 + 1)
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
- Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
- Если в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
А теперь закрепляем решение примеров на порядок действий на тренажерах!
Учебник Моро 4 класс 1 часть. Страница 6
Четыре арифметических действия: сложение, вычитание, умножение, деление
Упражнения
11. Рассмотри выражения и объясни, почему действия следует выполнять в порядке, указанном синими цифрами.
Комментарий: правильный порядок выполнения действий в выражении можно посмотреть на странице 103.
12. В каждом выражении сначала укажи порядок выполнения действий, а потом вычисли его значение.

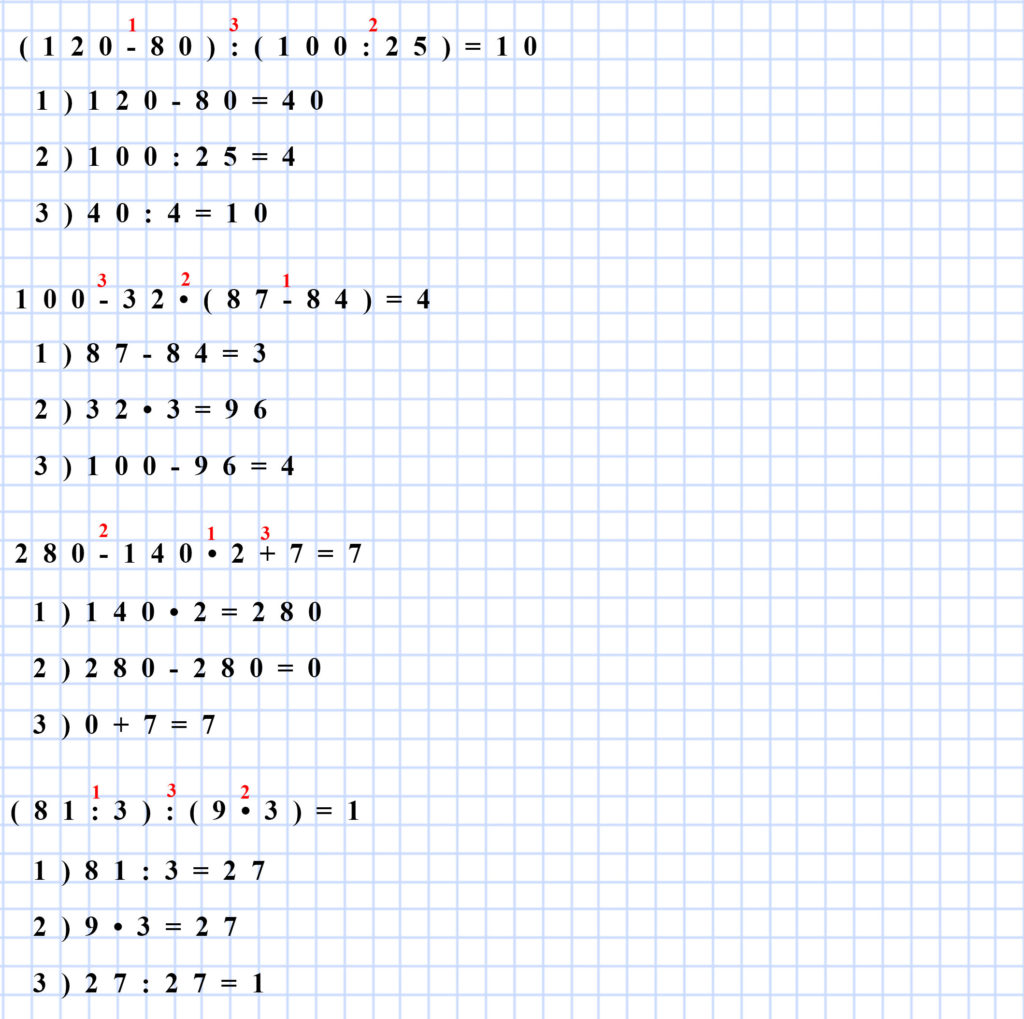
13. У Нины было 50 р. и ещё 8 монет, по 5 р. каждая. Сколько всего денег было у Нины?

1) 5 • 8 = 40 (рублей) — было у Нины в монетах.
2) 50 + 40 = 90 (рублей) — было всего денег.
Ответ: У Нины всего было 90 рублей.
14. В 2 одинаковых спальных вагонах поезда 120 мест. Сколько мест в 7 таких вагонах? в 10 таких вагонах?
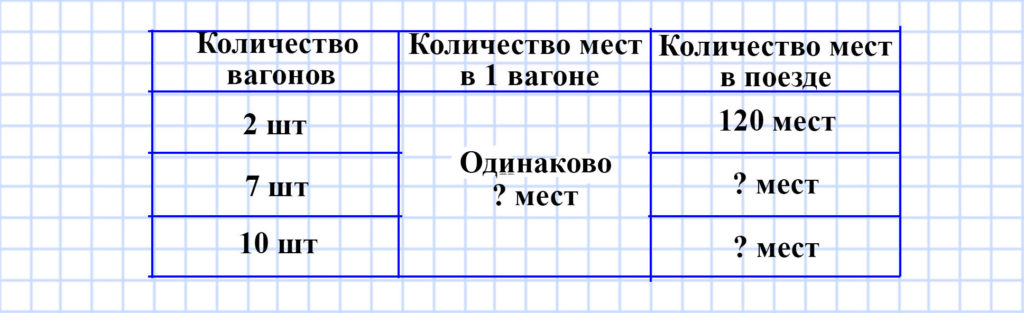
1) 120 : 2 = 60 (мест) — в одном спальном вагоне.
2) 60 • 7 = 420 (мест) — в 7 спальных вагонах.
3) 60 • 10 = 600 (мест) — в 10 спальных вагонах.
Ответ: в семи вагонах 420 мест, в десяти вагонах 600 мест.
Четыре арифметических действия: сложение, вычитание, умножение, деление
Рассмотри выражения и объясни, почему действия следует выполнять в порядке, указанном синими цифрами.
320 : (60 − 52) ∙ 6 (820 + − (310 − 60) 230 + (170 + 40 : 2) (420 + 16 ∙ 5) : 100 При вычислении числовых выражений сначала выполняют действия умножения и деления, а затем сложения и вычитания, слева направо. При наличии скобок вычисляют сначала значение выражения в них. Если выражение содержит несколько пар скобок, то сначала находят значения выражений в скобках (слева направо), а затем выполняют действия по первым двум правилам.
В каждом выражении сначала укажи порядок выполнения действий, а потом вычисли его значение.
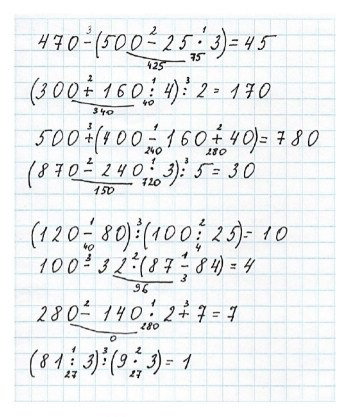
Другой способ оформления:
1) 25 ∙ 3 = 75 2) 500 – 75 = 425 3) 470 – 425 = 45
1) 160 : 4 = 40 2) 300 + 40 = 340 3) 340 : 2 = 170
1) 400 – 160 = 240 2) 240 + 40 = 280 3) 500 + 280 = 780
1) 240 ∙ 3 = 720 2) 870 – 720 = 150 3) 150 : 5 = 30
1) 120 – 80 = 40 2) 100 : 25 = 4 3) 40 : 4 = 10
1) 87 – 84 = 3 2) 32 ∙ 3 = 96 3) 100 – 96 = 4
1) 140 ∙ 2 = 280 2) 280 – 280 = 0 3) 0 + 7 = 7
1) 81 : 3 = 27 2) 9 ∙ 3 = 27 3) 27 : 27 = 1
У Нины было 50 р. и ещё 8 монет, по 5 р. каждая. Сколько денег было у Нины?
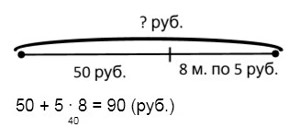
Ответ: 90 рублей было всего.
В 2 одинаковых спальных вагонах поезда 120 мест. Сколько мест в 7 таких вагонах? В 10 таких вагонах?

1) 120 : 2 = 60 (м.) – в одном вагоне. 2) 60 ∙ 7 = 420 (м.) – в семи вагонах. 3) 60 ∙ 10 = 600 (м.) – в десяти вагонах. Ответ: 420 мест и 600 мест.
Числа от 1 до 100 Умножение и деление (продолжение) Деление с остатком Ответы к стр. 32
1. Выполни деление с остатком и проверь:
50 15 = 3 (ост. 5) 89 22 = 4 (ост. 1)
15 • 3 + 5 = 50 22 • 4 + 1 = 89
18 27 = 0 (ост. 18) 75 18 = 4 (ост. 3)
27 • 0 + 18 = 18 18 • 4 + 3 = 75
100 30 = 3 (ост. 10) 57 42 = 1 (ост. 15)
30 • 3 + 10 = 100 42 • 1 + 15 = 57
76 20 = 3 (ост. 16) 28 17 = 1 (ост. 11)
3 • 20 + 16 = 76 1 • 17 + 11 = 28
25 26 = 0 (ост. 25) 9 13 = 0 (ост. 9)
26 • 0 + 25 = 25 13 • 0 + 9 = 9
2.
| A | 72 | 72 | 72 | 72 | 72 | 72 | 72 |
| B | 2 | 3 | 4 | 6 | 8 | 1 | 72 |
| A b | 36 | 24 | 18 | 12 | 9 | 72 | 1 |
3. Половину пути от дома до школы мальчик прошёл за 15 мин, а на остальной путь он затратил на 6 мин больше. Сколько времени он затратил на весь путь до школы?
1) 15 + 6 = 21 (мин) — на остальной путь
2) 15 + 21 = 36 (мин)
О т в е т: на весь путь до школы мальчик затратил 36 мин.
4. Начерти квадрат, площадь которого равна 4 см 2 . Раскрась его четвёртую часть. Покажи, как это можно сделать по-разному. Сколько квадратных сантиметров раскрашено? Чему равна площадь нераскрашенной части?
Раскрашен 1 см 2 . Площадь нераскрашенной части 3 см 2 .
5.
45 15 = 3 78 6 • 3 = 39 100 — 2 • 18 = 64
99 33 = 3 51 3 • 4 = 68 100 — 3 • 18 = 46
80 16 = 5 84 4 • 3 = 63 100 — 4 • 18 = 28
(34 + 36) 10 = 7
(75 — 33) 3 = 14
(82 — 16) 33 = 2
6. Измерь стороны многоугольников в миллиметрах и найди периметр каждого из них.
1) 24 • 4 = 96 мм 2) 33 • 3 = 99 мм 3) 15 • 6 = 90 мм
7. Используя только цифры 1, 2, 3, 4, 5, 6, 7 и не повторяя ни одну из них, составь такие 4 числа, чтобы при их сложении получилось 100.
2 + 17 + 35 + 46 = 100 6 + 15 + 32 + 47 = 100
5 + 12 + 36 + 47 = 100 7 + 14 + 23 + 56 = 100
6 + 15 + 37 + 42 = 100 7 + 16 + 35 + 42 = 100
Выполни проверку деления с остатком.
65 20 = 3 (ост. 5) 39 12 = 3 (ост. 3)
20 • 3 + 5 = 65 12 • 3 + 3 = 39
Раскрашен 1 см 2 . Площадь нераскрашенной части 3 см 2 .
3 класс. Моро. Учебник №2. Ответы к стр. 32
1. Выполни деление с остатком и проверь:
50 15 = 3 (ост. 5) 89 22 = 4 (ост. 1)
15 • 3 + 5 = 50 22 • 4 + 1 = 89
18 27 = 0 (ост. 18) 75 18 = 4 (ост. 3)
27 • 0 + 18 = 18 18 • 4 + 3 = 75
100 30 = 3 (ост. 10) 57 42 = 1 (ост. 15)
30 • 3 + 10 = 100 42 • 1 + 15 = 57
76 20 = 3 (ост. 16) 28 17 = 1 (ост. 11)
3 • 20 + 16 = 76 1 • 17 + 11 = 28
25 26 = 0 (ост. 25) 9 13 = 0 (ост. 9)
26 • 0 + 25 = 25 13 • 0 + 9 = 9
2.
| A | 72 | 72 | 72 | 72 | 72 | 72 | 72 |
| B | 2 | 3 | 4 | 6 | 8 | 1 | 72 |
| A b | 36 | 24 | 18 | 12 | 9 | 72 | 1 |
3. Половину пути от дома до школы мальчик прошёл за 15 мин, а на остальной путь он затратил на 6 мин больше. Сколько времени он затратил на весь путь до школы?
1) 15 + 6 = 21 (мин) — на остальной путь
2) 15 + 21 = 36 (мин)
О т в е т: на весь путь до школы мальчик затратил 36 мин.
4. Начерти квадрат, площадь которого равна 4 см 2 . Раскрась его четвёртую часть. Покажи, как это можно сделать по-разному. Сколько квадратных сантиметров раскрашено? Чему равна площадь нераскрашенной части?
Раскрашен 1 см 2 . Площадь нераскрашенной части 3 см 2 .
5.
45 15 = 3 78 6 • 3 = 39 100 — 2 • 18 = 64
99 33 = 3 51 3 • 4 = 68 100 — 3 • 18 = 46
80 16 = 5 84 4 • 3 = 63 100 — 4 • 18 = 28
(34 + 36) 10 = 7
(75 — 33) 3 = 14
(82 — 16) 33 = 2
6. Измерь стороны многоугольников в миллиметрах и найди периметр каждого из них.
1) 24 • 4 = 96 мм 2) 33 • 3 = 99 мм 3) 15 • 6 = 90 мм
7. Используя только цифры 1, 2, 3, 4, 5, 6, 7 и не повторяя ни одну из них, составь такие 4 числа, чтобы при их сложении получилось 100.
2 + 17 + 35 + 46 = 100 6 + 15 + 32 + 47 = 100
5 + 12 + 36 + 47 = 100 7 + 14 + 23 + 56 = 100
6 + 15 + 37 + 42 = 100 7 + 16 + 35 + 42 = 100
Выполни проверку деления с остатком.
65 20 = 3 (ост. 5) 39 12 = 3 (ост. 3)
20 • 3 + 5 = 65 12 • 3 + 3 = 39
Числа от 1 до 100 Умножение и деление (продолжение) Деление с остатком Ответы к стр. 32
Выполни деление с остатком и проверь.
18.05.2017 15:49:05
2017-05-18 15:49:05
Учитель начальных классов
2 класс. Математика. ТЕМА: Выражения со скобками
ТЕМА: Выражения со скобками
Математический диктант. Запиши каллиграфически результаты через запятую.
· Найди сумму чисел 7 и 4.
· Найди разность чисел 13 и 5.
· К какому числу нужно прибавить 3, чтобы получить 11?
· Из какого числа надо вычесть 4, чтобы получить 8?
· Слагаемые 9 и 5. Найди сумму.
· Уменьшаемое 13, вычитаемое 4. Чему равна разность?
· На сколько 11 больше 3?
· На сколько 4 меньше 12?
· Сумма равна 14, первое слагаемое 5. Чему равно второе?
· Первое число 11, второе на 2 меньше. Чему равно второе?
· Первое число 8, второе на 5 больше. Чему равно второе?
· На сколько надо увеличить 9, чтобы получить 14?
2) Вставь пропущенные знаки действий «+» или « — ».
· 5 … 4 … 3 … 2 … 1 … = 3
· 5 … 4 … 3 … 2 … 1 … = 5
3) У дощечки было 4 угла, один отпилили. Сколько углов осталось? Ответ покажи, начертив эту фигуру.
4) ПРАВИЛО: Если надо прибавить или вычесть сумму либо разность , то ее записывают в скобках.
Учись правильно читать выражения со скобками:
К числу 8 прибавить разность 7 и 5. 8 + (7 – 5)
Из числа 12 вычесть сумму 6 и 4. 12 – (6 + 4)
ЗАДАНИЕ: Запиши выражения, используя скобки. Научись правильно читать их!
· К сумме чисел 2 и 6 прибавить 2.
· Из числа 9 вычесть сумму 5 и 2.
· К числу 3 прибавить разность 7 и 6.
· К числу 4 прибавить сумму 2 и 3.
5) Какое выражение записано в скобках – сумма или разность? Прочитай выражения, как мы только что учились.
70 – (60 – 50) 40 – (80 – 70) 84 + (7 – 6) (65 – 5) – 20 (90 — 19) – 8 99 – (19 – 10)
6) Лена и Саша находили значения выражений по-разному. Объясни, как каждый из них рассуждал. Почему результаты вычислений получились одинаковыми?
Лена: 6 + 1 + 3 = (6 + 1) + 3 = 10 Саша: 6 + 1 + 3 = 6 + (1 + 3) = 10
ВЫВОД: Числа можно складывать в любом порядке!
7) Как разными способами можно найти значение суммы: 7 + 1 + 3?
Прокомментируй запись: 7 + (1 + 3) = (7 + 1) + 3. Сравни записи выражений.
Сделай предположение о значениях этих выражений. Каков вывод можно сделать?
В выражении со скобками первыми выполняют действия в скобках.
В выражении без скобок действия выполняют так, как они записаны, — слева направо.
ЗАДАНИЕ: Прочитай выражения, запиши, укажи над каждым действием порядок выполнения действий .
6 + (12 – 2) 8 – (4 + 2) (34 + 12) – 23 56 – 43 + 21 45 – 12 + 22
34 + (67 – 55) 45 – (3 + 2) (44 + 22) – 6 42 – (36 – 6) 44 + 6 – 22
9) Вычисли, соблюдая порядок выполнения действий, подписывая промежуточный ответ.
24 + ( 9 – 7) 7 + (9 – 6)
89 – (67 – 55) 8 — (4 + 3)
(45 – 32) + 23 9 – (5 – 4)
10) Работа по учебнику: с. 40 № 222, 223, 224
11) Домашнее задание: выучить все правила! Реши № 225, 226.
Источник




























