ГДЗ по Математике за 5 класс Виленкин Н.Я., Жохов В.И. часть 1, 2 ФГОС
авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И..
Издательство: Мнемозина 2018 год.
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 5 класс Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. часть 1, 2. Ответы сделаны к книге 2018 года от Мнемозина ФГОС
ГДЗ к учебнику по математике за 5 класс Виленкин Н.Я. (синий) можно посмотреть тут.
ГДЗ к тестам по математике за 5 класс Рудницкая В.Н. можно посмотреть тут.
ГДЗ к рабочей тетради по математике за 5 класс Рудницкая В.Н. можно посмотреть тут.
ГДЗ к дидактическим материалам по математике за 5 класс Попов М.А. можно посмотреть тут.
ГДЗ к дидактическим материалам по математике за 5 класс Чесноков А.С. можно посмотреть тут.
ГДЗ к рабочей тетради по математике за 5 класс Ерина Т.М. можно посмотреть тут.
ГДЗ к рабочей тетради Универсальные учебные действия по математике за 5 класс Ерина Т.М. можно посмотреть тут.
ГДЗ к контрольным работам по математике за 5 класс Жохов В.И. можно посмотреть тут.
ГДЗ к математическому тренажёру за 5 класс Жохов В.И. можно посмотреть тут.
ГДЗ к рабочей тетради по математике за 5 класс Лебединцева Е.А. можно посмотреть тут.
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206.
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.556>206, поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на , 1, 2, 3.. и получаем:
206·=<556; 206·1=206<556; 206·2=412<556; 206·3=618>556
618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144. Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442.
Повторяем с ним пункты 2-4. Получаем:
206·5=1030<1442; 206·6=1236<1442; 206·7=1442
Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
Ответ: 27
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34.
Ответ: 7002
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Часть 1:
Числа от 1 до 1000Нумерация
1
2
3
4
5
6
7
8
9
10
?
Четыре арифметических действия: сложение, вычитание, умножение, деление
11
12
13
14
15
16
17
18
19
20
21
22
?
23
24
25
26
27
28
?
29
30
31
32
33
34
35
36
?
37
38
39
40
41
42
43
?
44
45
46
47
48
49
50
51
52
53
?
54
55
56
57
58
59
?
60
61
62
63
64
65
66
67
?
68
69
70
71
72
73
?
74
75
76
77
78
79
80
?
Диаграммы
81
82
83
Страница 18. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Страница 19. Вопросы для повторения
1
2
3
4
Страница 20. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
12
Числа, которые больше 1000Нумерация
84
85
86
87
88
89
90
91
92
93
?
94
95
96
97
98
99
?
100
101
102
103
104
105
106
?
107
108
109
110
111
112
113
114
115
116
?
117
118
119
120
121
122
123
124
?
125
126
127
128
129
130
131
132
133
?
134
135
136
137
138
139
140
141
142
?
143
144
145
146
147
Страница 31. Странички для любознательных
1
2
3
Страница 34. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Страница 35. Вопросы для повторения
1
2
3
4
5
6
7
Величины
148
149
150
151
152
153
154
155
?
156
157
158
159
160
161
162
163
164
165
?
166
167
168
169
170
171
172
173
174
175
176
177
?
178
179
180
181
182
183
184
185
186
187
188
189
190
?
191
192
193
194
195
196
197
198
199
?
200
201
202
203
204
205
206
207
208
?
209
210
211
212
213
214
215
216
?
217
218
219
220
221
222
?
223
224
225
226
227
228
229
230
?
231
232
233
234
235
236
237
238
?
239
240
241
242
243
244
245
?
246
247
248
249
250
251
252
253
?
254
255
256
257
258
259
Страница 53. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Страница 55. Вопросы для повторения
1
2
3
Страница 58. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
10
Вариант 2
1
2
3
4
5
6
7
8
9
10
Сложение и вычитание
260
261
262
263
264
265
266
?
267
268
269
270
271
272
273
274
275
?
276
277
278
279
280
281
282
?
283
284
285
286
287
288
289
290
?
291
292
293
294
295
?
296
297
298
299
300
301
302
303
304
305
?
306
307
308
309
310
311
312
?
313
314
315
316
317
318
?
319
320
321
322
323
324
Страница 69. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
Страница 70. Странички для любознательных
1
2
3
4
Страница 71. Задачи — Расчеты
1
2
Страница 72. Что узнали. Чему научились
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Страница 73. Вопросы для повторения
1
2
3
4
5
6
Страница 74. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
10
Вариант 2
1
2
3
4
5
6
7
8
9
10
Умножение и деление
325
326
327
328
329
330
331
332
?
333
334
335
336
337
338
339
?
340
341
342
343
344
345
346
347
348
349
?
350
351
352
353
354
355
356
?
357
358
359
360
361
362
?
363
364
365
366
367
368
369
370
371
?
372
373
374
375
?
376
377
378
379
?
380
381
382
383
384
385
386
387
?
388
389
390
391
392
393
394
?
395
396
397
398
399
400
401
402
403
?
404
405
406
407
408
409
410
?
411
412
413
414
415
416
417
?
418
419
420
421
422
423
424
425
?
426
427
428
429
430
431
432
433
434
435
436
Страница 91. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Страница 95. Вопросы для повторения
1
2
3
4
5
6
7
8
Страница 96. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
Вариант 2
1
2
3
4
5
6
7
8
9
Тексты для контрольных работСтраница 98. Задания базового уровня
1
2
3
4
5
6
7
8
Страница 99. Задания повышенного уровня сложности
1
2
3
4
5
6
7
8
9
Часть 1:
стр. 4
стр. 5
стр. 6
стр. 7
стр. 8
стр. 9
стр. 10
стр. 11
стр. 12
стр. 13
стр. 14
стр. 15
стр. 16
стр. 17
стр. 18
стр. 19
стр. 20
стр. 21
стр. 22
стр. 23
стр. 24
стр. 25
стр. 26
стр. 27
стр. 28
стр. 29
стр. 30
стр. 31
стр. 32
стр. 33
стр. 34
стр. 35
стр. 36
стр. 37
стр. 38
стр. 39
стр. 40
стр. 41
стр. 42
стр. 43
стр. 44
стр. 45
стр. 46
стр. 47
стр. 48
стр. 49
стр. 50
стр. 51
стр. 52
стр. 53
стр. 54
стр. 55
стр. 56
стр. 57
стр. 58
стр. 59
стр. 60
стр. 61
стр. 62
стр. 63
стр. 64
стр. 65
стр. 66
стр. 67
стр. 68
стр. 69
стр. 70
стр. 71
стр. 72
стр. 73
стр. 74
стр. 75
стр. 76
стр. 77
стр. 78
стр. 79
стр. 80
стр. 81
стр. 82
стр. 83
стр. 84
стр. 85
стр. 86
стр. 87
стр. 88
стр. 89
стр. 90
стр. 91
стр. 92
стр. 93
стр. 94
стр. 95
стр. 96
стр. 97
стр. 98
стр. 99
Ответы к стр. 86
Продолжаем учиться решать задачи и выполнять вычисления.
395. Два куска одинаковой ткани стоят 360 р. В одном из них 5 м, а в другом − 4 м.Сколько стоит каждый кусок ткани?
1) 5 + 4 = 9 (м) − ткани всего в двух кусках
2) 360 9 = 40 (р.) − стоит 1 м ткани
3) 5 • 40 = 200 (р.) − стоит первый кусок
4) 4 • 40 = 160 (р.) − стоит второй кусок
Ответ: первый кусок стоит 200 р., а второй 160 р.
396. В одном мешке было 56 кг муки, а в другом − 24 кг муки. Эту муку расфасовали в 40 пакетов поровну. Сколько потребовалось пакетов для расфасовки муки из каждого мешка?
1) 56 + 24 = 80 (кг) − муки в двух мешках
2) 80 40 = 2 (кг) − муки в одном пакете
3) 56 2 = 28 (п.) − потребовалось для первого мешка
4) 24 2 = 12 (п.) − потребовалось для второго мешка
Ответ: для первого мешка потребовалось 28 пакетов, а для второго − 12 пакетов.
397. Определи заранее, сколько цифр должно получится в записи частного и выполни деление.6336 : 2 58135 : 7 251052 : 6 136012 : 46336 : 9 34472 : 8 411258 : 3 254105 : 5
Надо разделить 6336 на 2.
В записи частного будет 4 цифры, так как первая цифра делимого 6 больше делителя 2.— 6336|2 6 |3168 —03 2 _13 12 _16 16 0
Надо разделить 6336 на 9.
В записи частного будет 3 цифры, так как первая цифра делимого 6 меньше делителя 9.— 6336|9 63 |704 —036 36 0
Надо разделить 58135 на 7.
В записи частного будет 4 цифры, так как первая цифра делимого 5 меньше делителя 7.— 58135|7 56 |8305 —21 21 _035 35 0
Надо разделить 34472 на 8.
В записи частного будет 4 цифры, так как первая цифра делимого 3 меньше делителя 8.— 34472|8 32 |4309 —24 24 _072 72 0
Надо разделить 251052 на 6.
В записи частного будет 5 цифр, так как первая цифра делимого 2 меньше делителя 6.— 251052|6 24 |41842 —11 6 _50 48 _25 24 _12 12
Надо разделить 411258 на 3.
В записи частного будет 6 цифр, так как первая цифра делимого 4 больше делителя 3.— 411258|3 3 |137086 —11 9 _21 21 _025 24 _18 18
Надо разделить 136012 на 4.
В записи частного будет 5 цифр, так как первая цифра делимого 1 меньше делителя 4.— 136012|4 12 |34003 —16 16 _0012 12 0
Надо разделить 254105 на 5.
В записи частного будет 5 цифр, так как первая цифра делимого 2 меньше делителя 5.— 254105|5 25 |50821 —041 40 _10 10 _05 5 0
398. Ребята заполнили водой два больших аквариума: в один они влили 300 л воды, а в другой − 312 л. Сколько ведер воды им пришлось для этого принести? Дополни задачу недостающими данными и реши ее.
Чтобы решить задачу, надо знать, сколько литров воды вмещает одно ведро.
Ребята заполнили водой два больших аквариума: в один они влили 300 л воды, а в другой − 312 л. Сколько ведер воды им пришлось для этого принести, если одно ведро вмещает 12 л воды?
1) 300 + 312 = 612 (л) − воды в двух аквариумах
2) 612 12 = 51 (в.) − понадобилось для наполнения аквариумов
Ответ: ребятам пришлось принести 51 ведро воды.
399.
23 м 06 см = 23 • 100 + 6 = 2300 + 6 = 2306 см
1 мин 6 с = 1 • 60 + 6 = 66 с
1 ч 45 мин = 1 • 60 + 45 = 105 мин
2355 кг = 2000 + 355 = 2000 1000 + 355 = 2 т 355 кг
62335 кг = 62000 + 335 = 62000 1000 + 335 = 62 т 335 кг
584 мм = 580 + 4 = 580 10 + 4 = 58 см 4 мм
400. 10 км 875 м + 925 м 17 м 30 см • 6 12 т 015 кг − 98 кг 25 ц 80 кг : 3
10 км 875 м + 925 м = 11 км 800 м+10875 925 11800
12 т 015 кг − 98 кг = 11 т 917 кг_12015 98 11917
17 м 30 см • 6 = 103 м 80 см×1730 6
10380
25 ц 80 кг 3 = 8 ц 60 кг— 2580|3 24 |860 —18 18 0
401. Реши только те уравнения, в которых неизвестное число должно быть найдено делением.x : 9 = 900 100 • x = 6800 101 + x = 101x • 5 = 4500 7000 : x = 100 x − = 999
x • 5 = 4500x = 4500 5x = 900
100 • x = 6800x = 6800 100x = 68
7000 x = 100x = 7000 100x = 70
402. Вычисли и выполни проверку:1) 201500 : 5 25600 : 8 3070 • 82) 67030 + 15097 + 4378 70100 − 29306
— 201500|5 Проверка: × 40300 6 |40300 5 —11 201500 9 _25 24 _18 18
— 25600|8 Проверка: × 3200 24 |3200 8 —16 25600 16 0
× 3070 Проверка: _ 24560|8 8 24 |307024560 _056 56 0
67030
+ 15097 4378 86505
Проверка: _86505 _19475 67030 15097 19475 4378
_70100 Проверка: +40794 29306 29306 40794 70100
403. Во время экскурсии в один автобус сели 48 человек, а в другой − на 6 человек меньше. Сколько человек должны перейти из первого автобуса во второй, чтобы в них пассажиров стало поровну?
1) 48 − 6 = 42 (чел.) − во втором автобусе
2) 48 + 42 = 90 (чел.) − в двух автобусах
3) 90 2 = 45 (чел.) − поровну в автобусах
4) 48 — 45 = 3 (чел.) — должно перейти
Ответ: из первого автобуса во второй должны перейти 3 человека.
Вычисли. 8 м2 26 дм2 + 74 дм2 9 см 2 мм • 5
1) 8 м2 26 дм2 + 74 дм2 = 8 м2 + 26 дм2 + 74 дм2 = 8 м2 + (26 дм2 + 74 дм2) = 8 м2 + 100 дм2 = 8 м2 + 1 м2 = 9 м2
2) 9 см 2 мм • 5 = (9 см + 2 мм) • 5 = 9 см • 5 + 2 мм • 5 = 45 см + 10 мм = 45 см + 1 см = 46 см
ЗАДАНИЕ НА ПОЛЯХРебус
×5384 ×7329 3 9
16152 65961
| ← Предыдущая | Следующая → |
Решение задач с единицами площади
Ребята, взрослые люди часто испытывают досаду, занимаясь ремонтом дома или квартиры. Почему? Знакома ситуация, когда чуть-чуть не хватило краски или обоев? Нужно срочно бежать в магазин, чтобы купить недостающие материалы. Можно ли этого избежать? Конечно, можно! Главное, правильно выполнить расчеты. Например, правильно измерить площадь пола под покраску или площадь стен под обои.
Задача
В комнате длиной 7 м и шириной 8 м укладывают на пол ламинат квадратами 50х50 см. Сколько штук ламината потребуется для этой комнаты?
Подсказка. Вычислите площадь комнаты и площадь одного квадрата ламината. Одинаковые ли единицы площади вы использовали? Выразите квадратные метры в квадратных сантиметрах.
Решите задачу самостоятельно.
Проверь себя.
S пола = 7 ∙ 8 = 56 (м²)
S лам. = 50 ∙50 = 2 500 (см²)
1 м² = 10 000 см²
10 000 : 2 500 = 4 (шт.) – ламината в 1 м².
56 ∙ 4 = 224 (шт.) – ламината потребуется.
Ответ: 224 штук ламината.
Задача
Для покраски пола комнаты площадью 35 м² купили 3 кг краски. Хватит ли этой краски, если на 1 м² пола расходуется 100 г краски.
Выразим 3 кг в граммах.
1 кг = 1 000 г
3 кг = 3 000 г
35 ∙ 100 = 3 500 (г) – краски потребуется.
3 500 – 3000 = 500 (г) – краски не хватит для покраски пола.
Ответ: 500 г краски не хватит.
Решите аналогичную задачу самостоятельно и проверьте по образцу.
Задача
Стены комнаты решили оклеить обоями. Площадь поверхности составляет 80 м². На одной стене есть окно – 3 м², а на другой – дверь занимает 4 м². Хватит ли 7 рулонов обоев, если в одном рулоне 10 м² обоев.
Проверь себя.
3 + 4 = 7 (м²) – занимают окно и дверь.
80 – 7 = 73 (м²) – нужно оклеить обоями.
7 ∙ 10 = 70 (м²) – в семи рулонах.
73 – 70 = 3 (м²) – обоев не хватит.
Ответ: не хватит 3 м².
Ребята, на уроке мы учились делить на трехзначное число без остатка и с остатком, решали сложные задачи с единицами площади. А теперь настало время подвести итоги! Устроим небольшое соревнование на звание «Знатока математики».
Решите примеры за одну минуту!
(12 543 – 3 890 + 15 498) ∙ 69 ∙ 0 ∙594 =
640 ∙5 ∙0 +640 : 1 – 630 =
? + 150 – 240 – 10 + 26 = 526
Проверь себя.
0, 10, 600.
Кому удалось справиться с заданием за одну минуту, может смело назвать себя большим молодцом!
В первом и втором выражениях самые наблюдательные заметили умножение на нуль (можно не вычислять все выражение, а ∙ 0 = 0).
В третьем выражении первое число можно быстро найти, вычисляя с конца обратным действием: 526 – 26 + 10 + 240 – 150 = 600
Часть 2:
стр. 4
стр. 5
стр. 6
стр. 7
стр. 8
стр. 9
стр. 10
стр. 11
стр. 12
стр. 13
стр. 14
стр. 15
стр. 16
стр. 17
стр. 18
стр. 19
стр. 20
стр. 21
стр. 22
стр. 23
стр. 24
стр. 25
стр. 26
стр. 27
стр. 28
стр. 29
стр. 30
стр. 31
стр. 32
стр. 33
стр. 34
стр. 35
стр. 36
стр. 37
стр. 38
стр. 39
стр. 40
стр. 41
стр. 42
стр. 43
стр. 44
стр. 45
стр. 46
стр. 47
стр. 48
стр. 49
стр. 50
стр. 51
стр. 52
стр. 53
стр. 54
стр. 55
стр. 56
стр. 57
стр. 58
стр. 59
стр. 60
стр. 61
стр. 62
стр. 63
стр. 64
стр. 65
стр. 66
стр. 67
стр. 68
стр. 69
стр. 70
стр. 71
стр. 72
стр. 73
стр. 74
стр. 75
стр. 76
стр. 77
стр. 78
стр. 79
стр. 80
стр. 81
стр. 82
стр. 83
стр. 84
стр. 85
стр. 86
стр. 87
стр. 88
стр. 89
стр. 90
стр. 91
стр. 92
стр. 93
стр. 94
стр. 95
стр. 96
стр. 97
стр. 98
стр. 99
стр. 100
стр. 101
стр. 102
стр. 103
стр. 104
стр. 105
стр. 106
стр. 107
стр. 108
стр. 109
стр. 110
стр. 111
стр. 112
стр. 113
стр. 115
стр. 116
Учебник Моро 4 класс. 1 часть. Страница 86
395. Два куска одинаковой ткани стоят 360 р. В одном из них 5 м, а в другом − 4 м. Сколько стоит каждый кусок ткани?
396. В одном мешке было 56 кг муки, а в другом − 24 кг муки. Эту муку расфасовали в 40 пакетов поровну. Сколько потребовалось пакетов для расфасовки муки из каждого мешка?
397. Определи заранее, сколько цифр должно получится в записи частного и выполни деление.
398. Ребята заполнили водой два больших аквариума: в один они влили 300 л воды, а в другой − 312 л. Сколько ведер воды им пришлось для этого принести? Дополни задачу недостающими данными и реши ее.
Недостающие данные — ёмкость одного ведра, на пример 6 л.
399. Реши:
23 м 06 см = 2 306 см 1 мин 6 с = 60 с • 1+ 6 с = 66 с 1 ч 45 мин = 60 мин • 1 + 45 мин = 105 мин
2 355 кг = 2 т 355 кг 62 335 кг = 62 т 335 кг 584 мм = 58 см 4 мм
400. Реши:
401. Реши только те уравнения, в которых неизвестное число должно быть найдено делением.
402. Вычисли и выполни проверку:
403. Во время экскурсии в один автобус сели 48 человек, а в другой − на 6 человек меньше. Сколько человек должны перейти из первого автобуса во второй, чтобы в них пассажиров стало поровну?
Ответы к стр. 77
Учимся выполнять умножение многозначного числа на однозначное.
Письменное умножение любого многозначного числа на однозначное выполняется так же, как умножение трёхзначного числа на однозначное: сначала умножают единицы, потом десятки, сотни и т. д.
Объясни, как выполнено умножение. × 5432 3 16296
Второй множитель подписываем под единицами первого множителя. Будем умножать начиная с единиц: 2 умножить на 3 — получится 6, подписываем под единицами. Умножаем десятки: 3 умножить на 3 — получится 9, подписываем 9 под десятками. Умножаем сотни: 4 умножить на 3 — получится 12 сотен – это 1 тысяча и 2 сотни: 2 сотни подписываем под сотнями, а 1 тысячу запоминаем. Умножаем тысячи: 5 умножить на 3 — получится 15, да еще 1 тысяча: получится 16. Записываем 16 ниже. Получаем ответ: 16 296.
2 т 375 кг • 3
2 т 375 кг = 2375 кг× 2375 3 7125
7125 кг = 7 т 125 кг
Сначала надо перевести величины к одной размерности (наименованию), затем умножить на однозначное число, как в предыдущем примере, и потом перевести полученный результат в исходные единицы исчисления: тонны и килограммы.
333. Выполни умножение, используя, когда это удобно, перестановку множителей.
1) 5124 • 2 6 • 274 23452 • 7 9 • 56492
2) 2 км 425 м • 8 18 ц 02 кг • 4 230 см2 • 4
1) × 5124 × 274 × 23452 × 56492 2 6 7 9 10248 1644 164164 508428
2) 2 км 425 м = 2425 м, 18 ц 02 кг = 1802 кг× 2425 × 1802 × 230 8 4 4 19400 7208 920
19400 м = 19 км 400 м, 7208 кг = 72 ц 08 кг
334. В куске 40 м полотна. От него отрезали полотна на 6 детских простыней, по 1 м 80 см на каждую, и на наволочки 10 м 20 см. Сколько метров полотна осталось?
1) 1 м 80 см • 6 = 180 см • 6 = 1080 см = 10 м 80 см (п.) − отрезали на детские простыни
2) 10 м 80 см + 10 м 20 см = 21 м (п.) − всего отрезали
3) 40 м − 21 м = 19 м (п.) — осталось
О т в е т: осталось 19 м полотна.
335. В мастерской сшили 6 простыней, расходуя на каждую по 2 м 20 см полотна, и 8 наволочек, расходуя на каждую по 1 м 25 см полотна.Поставь вопрос и реши задачу.
Сколько всего было израсходовано полотна?1) 2 м 20 см • 6 = 220 см • 6 = 1320 см = 13 м 20 см (п.) − израсходовали на простыни2) 1 м 25 см • 8 = 125 см • 8 = 1000 см = 10 м (п.) − израсходовали на наволочки3) 13 м 20 см + 10 м = 23 м 20 см
О т в е т: всего израсходовали 23 м 20 см полотна.
336. Папа прошел 500 м за 5 мин. Сколько километров он пройдет за 1 ч, если считать, что за каждую минуту он проходит одинаковое количество метров?
1) 500 5 = 100 (м) − проходит папа за 1 минуту2) 100 • 60 = 6000 (м) = 6 (км) − проходит папа за 1 ч
О т в е т: за 1 час папа пройдёт 6 км.
337.
35894 + 7068 − 9408 = 42962 − 9408 = 33554
+35894 — 42962 7068 9408 42962 33554
(90 + 1) • 100 − 64 4 = 91 • 100 − 64 4 = 9100 − 16 = 9084
98888 + (60100 − 7302) = 98888 + 52798 = 151686
—60100 — 98888 7302 52798 52798 151686
90 + 1 • (100 − 64) 4 = 90 + 36 4 = 90 + 9 = 99
338. 1) Сравни площади прямоугольников ABCD и KMOP.2) Сравни площади квадрата квадрата ABCD и треугольника KOP.
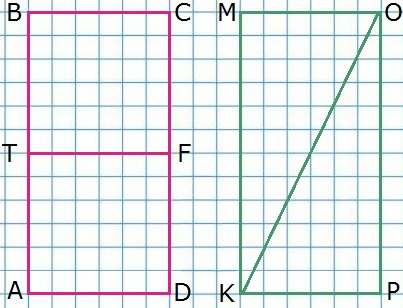АB = CD = KM = OP = 6 смBC = AD = MO = KP = 3 см
1) SABCD = SKMOP = 6 см • 3 см = 18 см2 — площади прямоугольников равны.
2) Квадрат ATFD − это половина прямоугольника ABCD, а треугольник KOP − половина прямоугольника KMOP. Площади этих прямоугольников равны 18 см2, следовательно, площадь квадрата равна площади треугольника.
339. В первой корзине было 25 кг слив, а во второй − на 7 кг меньше. Из первой корзины переложили во вторую 4 кг слив. Догадайся, в какой корзине слив стало больше и на сколько килограммов. Проверь себя вычислением.
Слив стало больше во второй корзине на 1 кг: 4 − 3 = 1 (кг).
1) 25 − 7 = 18 (кг) − слив было во второй корзине
2) 25 − 4 = 21 (кг) − стало в первой корзине
3) 18 + 4 = 22 (кг) − стало во второй корзине
21 < 22, значит, во второй корзине слив стало больше на: 22 − 21 = 1 (кг).
О т в е т: на 1 кг стало больше слив во второй корзине.
26 м 85 см • 7 = 2685 см • 7 = 18795 см = 187 м 95 см1 т 250 кг • 8 = 1250 кг • 8 = 10000 кг = 10 т190 мм2 • 5 = 950 мм2
× 2685 × 1250 × 190 7 8 5 18795 10000 950
| ← Предыдущая | Следующая → |
Математика 4 класс учебник Моро, Бантова 1 часть ответы — страница 86
️️Ответ к странице 86. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.
Решебник — страница 86Готовое домашнее задание
Два куска одинаковой ткани стоят 360 р. В одном из них 5 м, а в другом – 4 м. Сколько стоит каждый кусок ткани?
1) 5 + 4 = 9 (м) – ткани, общая длина. 2) 360 : 9 = 40 (р) – 1 метр ткани. 3) 5 ∙ 40 = 200 (р) – стоимость 1-ого куска. 4) 4 ∙ 40 = 160 (р) – стоимость 2-ого куска. Ответ: 1 к. т. – 200 руб., 2 к. т. – 160 руб.
В одном мешке было 56 кг муки, а в другом – 24 кг муки. Эту муку расфасовали в 40 пакетов поровну. Сколько потребовалось пакетов для расфасовки муки из каждого мешка?
1) 56 + 24 = 80 (кг) – в двух мешках. 2) 80 : 40 = 2 (кг) – в 1-ом пакете. 3) 56 : 2 = 28 (п.) – для 1-ого мешка. 4) 24 : 2 = 12 (п) – для 2-ого мешка. Ответ: 1-й м. – 28 п., 2-й м. – 12 п.
Определи заранее, сколько цифр должно получиться в записи частного, и выполни деление.
6336 : 2 = 3168 58135 : 7 = 8305 6336 : 9 = 704 34472 : 8 = 4309 251052 : 6 = 41842 136012 : 4 = 34003 411258 : 3 = 137086 254105 : 5 = 50821
Ребята заполнили водой два больших аквариума: в один они влили 300 л воды, а в другой – 312 л. Сколько вёдер воды им пришлось для этого принести? Дополни задачу недостающими данными и реши её.
В одно ведро вмещается 6 литров. 1) 300 : 6 = 50 (в) – воды, для первого акв. 2) 312 : 6 = 52 (в.) – воды, для второго акв. 3) 50 + 52 = 102 (в.) – всего. Ответ: 102 ведра воды. Или 1)300 + 312 = 612 литров воды влили в оба аквариума. 2)612 : 6 = 102 ведра воды понадобятся для того, чтобы наполнить оба аквариума. Ответ: 102 ведра.
23 м 06 см = 2306 см 1 мин 6 с = 66 с 1 ч 45 мин = 105 мин 2355 кг = 2 т 355 кг 62335 кг = 62 т 335 кг 584 мм = 58 см 4 мм
10 км 875 м + 925 м = 10875 м + 925 м = 11800 м = 11 км 925 м 12 т 015 кг − 98 кг = 12015 кг − 98 кг = 11917 кг = 11 т 917 кг 17 м 30 см ∙ 6 = 1730 см ∙ 6 = 10380 см = 103 м 80 см 25 ц 80 кг : 3 = 2580 кг : 3 = 860 кг = 8 ц 60 кг
Реши только те уравнения, в которых неизвестное число должно быть найдено делением.
х ∙ 5 = 4500 х = 4500 : 5 х = 900 100 ∙ х = 6800 х = 6800 : 100 х = 68 7000 : х = 100 х = 7000 : 100 х = 70
Вычисли и выполни проверку.
1) 201500 : 5 = 40300 Проверка: 40300 ∙ 5 = 201500 25600 : 8 = 3200 Проверка: 3200 ∙ 8 = 25600 3070 ∙ 8 = 24560 Проверка: 24560 : 8 = 3070 2) 67030 + 15097 + 4378 = 86505 Проверка: 86505 − 67030 − 4378 = 15097 70100 − 29306 = 40794 Проверка: 40794 + 29306 = 70100
Во время экскурсии в один автобус сели 48 человек, а в другой – на 6 человек меньше. Сколько человек должны перейти из первого автобуса во второй, чтобы в них пассажиров стало поровну?
1) 48 − 6 = 42 (п.) – сели в другой автобус. 2) 48 + 42 = 90 (п.) – в двух автобусах. 3) 90 : 2 = 45 (п.) – в каждом авт. 4) 48 − 45 = 3 (п.) – должны пересесть. Ответ: 3 человека.
Задание внизу страницы
8 м² 26 дм² + 74 дм² = 9 м² 9 см 2 мм ∙ 5 = 46 см
Часть 2:
Числа, которые больше 1000Умножение и деление на однозначное число (продолжение)
1
2
3
4
5
6
7
?
8
9
10
11
12
13
?
14
15
16
17
18
19
20
?
21
22
23
24
25
26
?
27
28
29
30
31
32
33
34
Страница 9. Задачи — Расчеты
1
2
3
Страница 10. Странички для любознательных
1
2
3
4
Умножение на числа, оканичвающиеся нулями
35
36
37
38
39
?
40
41
42
43
44
45
46
?
47
48
49
50
51
52
53
?
54
55
56
57
58
59
60
?
61
62
63
64
?
65
66
67
68
69
70
71
72
?
Страница 18. Странички для любознательных
1
2
3
4
5
6
Страница 20. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Страница 23. Вопросы для повторения
1
2
Страница 24. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
12
Деление на числа, оканчивающиеся нулями
73
74
75
76
77
?
78
79
80
81
82
83
84
85
86
87
?
88
89
90
91
92
93
94
?
95
96
97
98
99
100
101
?
102
103
104
105
106
107
108
?
109
110
111
112
113
?
114
115
116
117
118
119
?
120
121
122
123
124
?
125
126
127
128
?
129
130
131
132
133
134
135
136
137
138
Страница 35. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Страница 37. Вопросы для повторения
1
2
Страница 38. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
10
Вариант 2
1
2
3
4
5
6
7
8
9
10
Страница 40. Наши проекты
1
2
3
4
5
6
Умножение на двузначное и трехзначное число
139
140
141
142
143
144
145
?
146
147
148
149
150
151
152
153
154
155
?
156
157
158
159
160
?
161
162
163
164
165
166
167
168
?
169
170
171
172
173
?
174
175
176
177
178
179
180
181
?
182
183
184
?
185
186
187
188
189
190
?
191
192
193
194
195
196
197
?
198
199
200
201
202
203
204
?
Страница 52. Странички для любознательных
1
2
3
4
5
Страница 54. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Страница 56. Вопросы для повторения
1
2
Деление на двузначное и трехзначное число
205
206
207
208
209
210
?
211
212
213
214
215
216
217
218
?
219
220
221
222
223
224
225
?
226
227
228
229
230
231
?
232
233
234
235
236
237
?
238
239
240
241
242
243
244
245
246
?
247
248
249
250
251
252
253
254
255
?
256
257
258
259
260
261
262
263
264
?
265
266
267
268
269
?
270
271
272
273
274
275
276
277
278
Страница 67. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
Страница 68. Задачи — Расчеты
1
2
3
4
5
6
Страница 70. Что узнали. Чему научились
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Письменное деление на трехзначное число
279
280
281
282
283
?
284
285
286
287
288
289
?
290
291
292
293
294
295
296
297
298
?
299
300
301
302
303
304
305
306
307
?
308
309
310
311
312
313
314
315
?
316
317
318
319
320
321
322
?
Страница 78. Странички для любознательных
1
2
3
4
5
6
7
Страница 80. Готовимся к олимпиаде
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Страница 82. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Итоговое повторение всего изученногоСтраница 86. Нумерация
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Страница 89. Выражения и уравнения
1
2
3
4
5
6
7
8
Страница 90. Сложение и вычитание
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Страница 92. Умножение и деление
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Страница 94. Правила о порядке выполнения действий
1
2
3
4
5
6
7
Страница 95. Величины
1
2
3
4
5
6
Страница 96. Геометрические фигуры
1
2
3
4
5
6
7
8
9
10
11
12
Страница 97. Задачи
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
Страница 103. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Материал для расширения и углубления знанийСтраница 104. Доли
1
2
3
Страница 105. Единицы площади — ар и гектар
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Страница 108. Диагонали прямоугольника (квадрата) и их свойства
1
2
3
4
Страница 110. Куб
1
2
Страница 111. Прямоугольный параллелепипед
1
2
Страница 112. Пирамида
1
2
Страница 113. Цилиндр
1
2
Страница 113. Шар
1
2
Тексты для контрольных работСтраница 114. Задания базового уровня
1
2
3
4
5
6
7
8
Страница 115. Задания повышенного уровня сложности
1
2
3
4
5
6
7
8
9
Базовая информация
Деление — это сложная арифметическая операция, состоящая из делимого, делителя и результата — частного. Если под рукой нет устройства, позволяющего быстро выполнять расчеты, то рекомендуется выполнять действие в столбик аналогично умножению, сложению и вычитанию. Однако существуют некоторые особенности в алгоритмах.
Следует отметить, что арифметическая операция классифицируется на два типа: без остатка и с ним. Первый вариант предусматривает полное деление одной величины на другую без дробного значения. Если невозможно выполнить его без использования дроби, то говорят, что получена целая часть и некоторый остаток. Например, 7/3=2 (+1). Кроме того, существуют определенные правила — признаки делимости числовых величин.
Принцип составления чисел
В основном изучают деление двузначного на однозначное в 3 классе. Однако перед этим требуется знать принципы построения чисел. К ним относятся следующие:
- Число составляется из цифр.
- Цифры — математические символы, необходимые для составления чисел и представляющие количественные характеристики.
- Разряд — положение количественного математического символа, показывающее определенное значение.
- Любое значение или величина состоит из разрядов (единиц, десятков, сотен, тысяч и т. д. ).
Признаки деления
При величинах, являющимися внетабличными (отсутствуют в таблице умножения) делить столбиком двузначное число на однозначное очень просто. Для этого следует руководствоваться некоторыми правилами, к которым относятся такие:
- На нулевое значение делить нельзя, поскольку получается пустое множество.
- На 1 можно поделить любое число, т. е. р/1=р.
- При делении на двойку разряд единиц принимает только четные значения.
- Числовое значение делится на 3, когда сумма цифр разрядов делится на нее.
- На 4 величина делится нацело, когда алгебраическую сумму разрядов единиц и десятков можно разделить на это значение.
- Если разряд единиц эквивалентен 0 или 5, то, значит, и число делится на 5.
- На шесть можно разделить при выполнении 3 и 4 пунктов.
- Чтобы разделить на 7, нужно перемножить разряды десятков и единиц. Полученный результат — делится на семерку.
- Если величина делится на 2 и 4, то ее можно разделить на 8.
- Искомое числовое значение делится на девятку, когда алгебраическую сумму всех цифр, составляющих его, возможно поделить на этот делитель.
Классификация величин
Ученые классифицируют числа на простые и составные. Первые возможно поделить только на единицу и равное значение искомому, а составные — на любые значения, кроме 1 и эквивалентных им. Пример простого — 13 (13/1=13 и 13/13=1), а составного — 26 (26/1=26, 26/26=1, 26/2=13 и 26/13). Математики разработали специальный алгоритм, позволяющий правильно классифицировать искомую величину. Суть его состоит в том, что нужно пройтись по всем признакам деления («+» — делится, а «-» — невозможно разделить нацело). Например, требуется идентифицировать число 99:
- 1: +.
- 2: -.
- 3: + (9+9=18/3=6).
- 4: -.
- 5: -.
- 6: -.
- 7: -.
- 8: -.
- 9: + (9+9=18/2=9).
- 11: + (99/9=11, а 99/11=9 — правило переместительного свойства умножения).
- 99: 99/99=1.
Можно сделать выводы, что 99 — составная величина, поскольку делится не только на 1 и 99, но и на 9, 3 и 11. Однако для выявления принадлежности достаточно первых трех и последнего пунктов. Перебор множителей был произведен, чтобы учащиеся понимали суть метода.