Гдз решебник по окружающему миру 4 класс дмитриева, казаков рабочая тетрадь дом федорова

Среднее значение

Каждый из нас в жизни встречается с выражениями «в среднем», «средняя температура», «средний заработок». Что это значит?

Рассмотрим на конкретной задаче.

Три друга Иван, Костя и Владимир каждую среду идут вместе от школы до музыкальной студии, где учатся игре на гитаре. Иван от школы до студии насчитал 251 шаг. Костя – 248 шагов, а Владимир насчитал 254 шага. Сколько в среднем шагов от школы до музыкальной студии?

В математике существует понятие «среднее арифметическое». Чтобы найти среднее арифметическое в этой задаче, нужно сложить количество шагов трех друзей, а затем полученную сумму разделить на 3 (по количеству слагаемых).

251 + 248 + 254 = 753 шага.

753 : 3 = 251 шаг

Можно сказать, что от школы до музыкальной студии в среднем 251 шаг.

Составим алгоритм.

Например, найти среднее арифметическое чисел: 5, 8, 7, 4.

Находим сумму чисел 5 + 8 + 7 + 4 = 24

Количество слагаемых – 4, значит, полученную сумму разделим на 4.

24 : 4 = 6

Среднее арифметическое – 6.

Пользуясь алгоритмом, найдите среднее арифметическое чисел: 12, 10, 8.

Проверь себя.

12 + 10 + 8 = 30

30 : 3 = 10

Среднее арифметическое – 10.

Рассмотрим более сложную задачу на нахождение среднего арифметического.

Задача

В столовой детского сада для приготовления завтраков малышам расходовали молоко три дня по 20 л и два дня по 25 л. Сколько в среднем расходовали молока в день?

Решим задачу вместе.

Сначала узнаем, сколько всего молока израсходовали.

20 ∙ 3 + 25 ∙ 2 = 110 (л) – израсходовали всего.

Затем узнаем, сколько дней расходовали молоко на завтрак.

3 + 2 = 5(дн.) – расходовали молоко.

Осталось количество израсходованного молока разделить на число дней.

110 : 5 = 22 (л) – расходовали в среднем за день.

Попробуйте самостоятельно решить подобную задачу.

Задача

Для игрового уголка в классе родители закупили 3 настольные игры: «Пазлы», «Домино», «Математический тренажер». Игра «Пазлы» стоила 160 р., «Домино» – 210 р., а «Математический тренажер» – 230 р.. Найди среднюю стоимость настольной игры.

Проверь себя.

160 + 210 + 230 = 600 (р.) – заплатили за все игры.
600 : 3 = 200 (р.) – стоит в среднем одна настольная игра.
Ответ: 200 рублей

Зачем ученикам нужна математика?

К четвертому году обучения школьники уже научились считать, умножать и делить, строить простые геометрические фигуры и решать уравнения. Что же дальше? Этим вопросом задаются многие школьники, так как считают, что все необходимое они уже освоили. Но на самом деле программа по одному из самых сложных предметов предполагает еще большее углубление в материал. С каждым годом ученикам предстоит сталкиваться с более обширными темами и трудными алгоритмами. С «ГДЗ по математике 4 класс Рабочая тетрадь Петерсон (Просвещение) Учусь учиться» им будет легче усвоить учебный курс и сориентироваться в новой тематике.

Знание данной дисциплины позволит учащимся полноценно реализовать себя во взрослой жизни, так как она неразрывно связана с такими профессиональными сферами как:

Программирование.
Инженерия.
Банковское дело.
Менеджмент.
Строительство.

Чтобы получить хорошую профессию в будущем, необходимо уже сейчас приложить много усилий к тому, чтобы понять и запомнить все необходимые аспекты программы по математике. В случае затруднений всегда можно воспользоваться решебником, где изложены подробные пояснения по всему текущему курсу.

ВИДЕОУРОК

Объекты движения движутся в
одном направлении, выезжая из одного пункта одновременно.

Рассмотрим случай,
когда объекты движения могут двигаться в одном направлении, причём с различной
скоростью.

Например, из одного
пункта одновременно могут выехать велосипедист и мотоциклист, причём скорость
велосипедиста может составлять 20 км/час,
а скорость мотоциклиста – 40 км/час.

После начала
движения, через один час, мотоциклист будет впереди велосипедиста на 20 км. Это
связано с тем, что за один час он преодолевает на 20
км больше, чем велосипедист. Поэтому каждый час
расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать
километров. В данном случае 20 км/час являются скоростью удаления мотоциклиста от
велосипедиста. Через два часа расстояние, пройденное велосипедистом, будет
составлять 40
км. Мотоциклист же проедет 80
км, отдалившись от велосипедиста
ещё на 20
км. Тогда расстояние между ними
составит уже 40
км.

Чтобы найти
скорость удаления при движении в одном направлении, нужно из большей скорости
вычесть меньшую скорость.

В приведённом
примере, скорость удаления составляет 20 км/час.
Её можно найти путём вычитания скорости велосипедиста из скорости мотоциклиста.
Скорость велосипедиста составляла 20 км/час,
а скорость мотоциклиста – 40
км/час. Скорость
мотоциклиста больше, поэтому из 40 вычитаем
20.

40 км/час –
20
км/час = 20
км/час.

ЗАДАЧА:

Из города в одном и том же направлении выехали легковой
автомобиль и автобус. Скорость автомобиля
120
км/час, а скорость автобуса 80 км/час. Какое расстояние будет между ними через 1
час ?2
часа ?

РЕШЕНИЕ:

Найдём скорость удаления. Для этого из большей скорости
вычтем меньшую скорость

120 км/час – 80 км/час = 40 км/час.

Каждый час легковой автомобиль отдаляется от автобуса
на 40
километров. За один час расстояние между автомобилем и автобусом будет 40
км. За 2
часа в два раза больше

40 ∙ 2 = 80 (км).

ОТВЕТ:80 км

ЗАДАЧА:

Из одного пункта в одном направлении одновременно выехали
два мотоциклиста. Скорость одного 35 км/час,
а скорость другого составляла 80% скорости первого мотоциклиста. Какое
расстояние будет между ними через 5 часов ?

РЕШЕНИЕ:

Найдём скорость второго мотоциклиста. Она составляет 80% скорости первого
мотоциклиста. Поэтому чтобы найти скорость второго мотоциклиста, нужно
найти 80% от35 км/час.

35 ∙ 0,80 = 28 км/час.

Первый мотоциклист двигается на 7 км/час быстрее

35 км/час– 28
км/час =7 км/час.

За один час первый мотоциклист преодолевает на 7 км больше. С каждым часом он будет отдаляться от
второго мотоциклиста на эти 7 км. Через 5 час первый
мотоциклист пройдёт

35 ∙ 5 = 175(км),

а второй

28 ∙ 5 = 140(км),

Определим расстояние, которое будет между ними через 5
час

175 км– 140
км =35 км.

ОТВЕТ:35 км

ЗАДАЧА:

Автомобиль и автобус выехали одновременно из одного
пункта в одном направлении. Скорость автомобиля
53
км/час, скорость автобуса 41
км/час. Через сколько часов после выезда автомобиль будет впереди автобуса
на 48
км ?

РЕШЕНИЕ:

Найдём скорость удаления автомобиля от автобуса

53 км/час– 41
км/час =12 км/час.

С каждым часом автомобиль будет удаляться от автобуса
на 12
км. Чтобы узнать через сколько часов автомобиль будет впереди автобуса на 48
км, нужно определить сколько раз 48 км содержат
по 12
км

48 : 12 = 4 (час).

ОТВЕТ:4 час

ЗАДАЧА:

Из одного города одновременно в одном направлении
выехали грузовик со скоростью 48 км/год и
легковой автомобиль со скоростью 64 км/год. Каким будет расстояние между ними
через 3 часа после начала движения

Что есть в ГДЗ по математике?

Содержимое «ГДЗ по математике 4 класс Рабочая тетрадь Петерсон (Просвещение)» полностью соответствует оригинальному учебному пособию. Найти нужное упражнение не составит для школьников особого труда. Но прежде, чем заглядывать на страницы пособия, стоит попробовать самостоятельно решить домашнее задание и только после этого сверять их с теми ответами, что даны в решебнике. Такой подход обеспечит стабильное понимание материала и высокую успеваемость.

На станицах данного сборника дети найдут все необходимое, чтобы проверить свои работы:

подробные решения по всем номерам;
верные ответы;
дополнительные пояснения;
наглядные примеры.

Наши модераторы постоянно следят за тем, чтобы пользователи получали только достоверную и актуальную информацию. Сами решебники составлялись людьми, которые не один год проработали в сфере образования, поэтому в правильности написанного можно не сомневаться. Более того, пособие соответствует всем требованиям ФГОС, что практически приравнивает его к учебным материалам. Математику можно научиться понимать и ГДЗ поможет учащимся в этом.

Движение навстречу друг другу, движение в противоположных направлениях

Разберем наглядный пример. Пусть из одного города в противоположных направлениях движутся два автомобиля. Первая машина едет со скоростью 85 км/ч, а скорость второй составляет 60 км/ч. Попробуем вычислить расстояние, на которое будут удалены друг от друга эти автомобили через 2 часа в пути.

Получим, что первый автомобиль проедет за 2 часа 170 км. Расстояние, которое преодолеет второй автомобиль в течение 2 часов равно 120 км. Тогда расстояние между машинами, спустя 2 часа, составит 290 км.

Если решать задачу другим способом, то получится, что скорость удаления составит 145 км/ч. Расстояние при этом равно:

Скорость. Время. Расстояние

Скорость

Вы наблюдали, что вокруг нас постоянно что-то или кто-то движется. Некоторые объекты – быстро, а некоторые – совсем медленно. Например, по лесной тропе прогуливается человек, по шоссе едет автомобиль, по воздуху летит вертолет. Все они движутся. Но автомобиль движется быстрее, чем человек, а вертолет – быстрее автомобиля.

В математике, величиной характеризующей быстроту движения объектов называют скоростью.

Скорость движения – это расстояние, пройденное за единицу времени. Единицей времени может быть: 1 секунда, 1 минута, 1 час.

Давайте вместе разберем две простые задачи.

Легковая машина прошла 120 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько км прошла машина за 1 час?

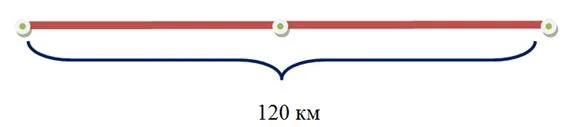
120 : 2 = 60 (км) – пройдет машина за 1 час.

Таким образом, скорость движения машины 60 км в час. Сокращенно запишем так:

60 км/ч.

Космический корабль пролетает 8 000 м за 1 секунду. Как по-другому записать его скорость?

Его скорость можно записать так: 8 000 м/с. Мы знаем, что 1 км = 1000 м, поэтому скорость корабля можно записать по-другому: 8 км/с.

Посмотрите скорость движения некоторых животных

Какое животное самое медленное, самое быстрое? Обратите внимание, что скорость можно записать по-разному: в зависимости от того, сколько сантиметров, метров, километров кто-то пролетает, проползает или пробегает за секунду, минуту, час

Время

С единицами времени вы уже знакомы. Это: секунда, минута, час, сутки, неделя, месяц, год, век.

Расстояние

Расстояние – это длина дороги, соединяющая начало и конец пути.

Расстояние измеряется в следующих единицах:

Миллиметр

Сантиметр

Дециметр

Метр

Километр

window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: ‘yandex_rtb_R-A-483726-10’, blockId: ‘R-A-483726-10’ }) })

Ребята участвовали в соревнованиях по бегу. Максим пробежал 200 м за 40 с, а Артем это же расстояние пробежал за 50 с. С какой скоростью бежал каждый из мальчиков?

Начертите таблицу, как в предыдущей задаче. Запишите величины в нужные ячейки. Поставьте знак вопроса. Пользуясь формулой, решите задачу самостоятельно.

Проверь себя.

v = S t

200 : 40 = 5 (м/с) – скорость движения Максима.

200 : 5 = 4 (м/с) – скорость движения Артема.

Ответ: 5 м/с, 4 м/с.

Решим еще одну задачу.

Два всадника отправились на прогулку на лошадях Рада и Снежка. Лошади преодолели одинаковое расстояние 30 км. Но двигались с разной скоростью. Рада бежала со скоростью 10 км/ч, а Снежка – 15 км/ч. Сколько времени длилась прогулка на Раде, и сколько времени – на Снежке?

Начертите таблицу, заполните ее ячейки. Пользуясь формулой, запишите решение.

Проверь себя.

t = S : v

30 : 10 = 3 (ч) – прогулка на Раде.

30 : 15 = 2 (ч) – прогулка на Снежке.

Ответ: 3 ч, 2 ч.

Сегодня на уроке мы запомнили формулы-ключи для решения задач на движение, узнали о скорости самых медленных и самых быстрых животных, научились находить среднее арифметическое. До скорых встреч, ребята!

Уроки арифметики на українській мові

Урок №2. Додавання натуральних чисел
Урок №3. Віднімання натуральних чисел
Урок №4. Таблиця множення
Урок №5. Множення натуральних чисел
Урок №6. Ділення натуральних чисел
Урок №8. Величини та їх вимірювання
Урок №10. Подільність чисел
Урок №13. Звичайні дроби
Урок №15. Додавання дробів
Урок №16. Віднімання дробів
Урок №17. Множення дробів
Урок №18. Ділення дробів
Урок №21. Кінечни десяткові дроби
Урок №22. Додавання десяткових дробів
Урок №23. Віднимання десяткових дробів
Урок №24. Множення десяткових дробів
Урок №25. Ділення десяткових дробів
Урок №18. Нескінченний десятковий дріб
Урок №19. Відношення величин
Урок №20. Пропорції
Урок №6. Відсотки
Урок №7. Відсотки (2)
Урок №12. Середнє арифметичне
Урок №14. Масштаб

Задачи на нахождение времени

Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км /ч. Через сколько часов после выхода пассажирского поезда эти поезда встретятся?
Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч. Через какое время они встретятся?
Максим и Саша вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут Рома догонит Максима и Сашу?
Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?
Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?
Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?
За какое время при движении против течения реки теплоход пройдет 204 км, если его собственная скорость 15 км/ч, а скорость течения в 5 раз меньше собственной скорости теплохода?
За какое время при движении против течения реки лодка пройдет 56 км, если скорость течения – 2 км/ч, а её собственная скорость на 8 км/ч больше скорости течения?
Сколько времени понадобится велосипедисту, чтобы проехать 78 км со скоростью 13 км/ч?
Пешеход прошел 12 км со скоростью 4 км/ч. Сколько времени он затратил на этот путь?
Расстояние между городами 930 км. Одновременно навстречу друг другу вышли 2 поезда. Скорость одного 45 км/ч, другого — 48 км/ч. Через сколько часов поезда встретились?
Велосипедист и пешеход отправились в путь одновременно в одном направлении из двух колхозов, расстояние между которыми 24 км. Велосипедист ехал вдогонку пешеходу со скоростью 11 км/ч, а пешеход шел со скоростью 5 км/ч. Через сколько часов после своего выезда велосипедист догонит пешехода?
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Из двух городов, расстояние между которыми 1800 км, одновременно навстречу друг другу вылетели 2 вертолета. Скорость первого вертолета равна 200 км/ч, а скорость второго составляет 80 % от скорости первого. Через сколько времени после вылета расстояние между вертолетами сократится до 720 км/ч?

Задачи на скорость сближения

При перемещении тел относительно друг друга в распространенных случаях необходимо определить их относительную скорость. Величина зависит от условий задачи:

относительная скорость равна сумме скоростей, когда рассматривается встречное движение тел;
относительная скорость равна разности скоростей, когда рассматривается однонаправленное движение тел.

Логично предположить, что расстояние между точками отправления равно сумме расстояний, которые преодолели автомобили. Первый автомобиль преодолел такой путь:

Второй автомобиль преодолел такой путь:

Тогда расстояние между точками составит:

72 + 48 = 120 (км)

Существует второй способ решения этой задачи, который считается наиболее рациональным. В этом случае воспользуемся формулой сложения скоростей:

60 + 40 = 100 (км/ч)

Если автомобили сближаются со скоростью 100 км/ч, то расстояние составит: