Затейники стр. 53. литературное чтение 2 класс

Содержание

Слайд 1

Числа от 1 до 1000Устные приёмы
умножения и деления

Автор Пономарева Людмила Владимировна,
Учитель начальных классов,
МКОУ «Средняя школа № 5 с углубленным изучением отдельных предметов»
Г. Фролово
интерактивный тренажёр
3 класс
Слайд 2

Мышата хотят помешать коту выполнить задания.
Ребята! Поможем Леопольду!
Читайте задания, выбирайте
правильные ответы.
Для перехода на следующий слайд –
нажимайте на Леопольда.
Удачи!
Слайд 3

201
820
50
82
Чему равно произведение чисел 205 и 4?

209

Ой!
Ошибка!

Верно!
Слайд 4

в 495
в 11
в 10
в 100
Во сколько раз 500 больше, чем 5?

в 25

Ой!
Ошибка!

Верно!
Слайд 5

915
905
5
308
Увеличь 305 в 3 раза.

100

Ой!
Ошибка!

Верно!
Слайд 6

200
2
20
840
Чему равно частное чисел 800 и 40?

760

Ой!
Ошибка!

Верно!
Слайд 7

12
110
847
833
Уменьши 840 в 7 раз.

120

Ой!
Ошибка!

Верно!
Слайд 8

на 4
на 5
на 40
на 100
На сколько надо умножить 250, чтобы получилась одна тысяча?

на 10

Ой!
Ошибка!

Верно!
Слайд 9

5
25
500
50
Чему равно частное чисел 1000 и 20?

800

Ой!
Ошибка!

Верно!
Слайд 10

23
110
575
120
Задуманное число разделили на 5 и получилось 115. Какое число задумали?

125

Ой!
Ошибка!

Верно!
Слайд 11

222
20
111
200
Какое число надо умножить на 2, чтобы получить 444?

888

Ой!
Ошибка!

Верно!
Слайд 12

в 60
в 6
в 840
в 4
Во сколько раз 720 больше, чем 120?

в 600

Ой!
Ошибка!

Верно!
Слайд 13

в 2
в 22
в 333
в 3
Во сколько раз 333 меньше, чем 666?

в 222

Ой!
Ошибка!

Верно!
Слайд 14

в 480
в 700
в 70
в 7
Во сколько раз надо увеличить 60, чтобы получилось 420?

в 6

Ой!
Ошибка!

Верно!
Слайд 15

5
3
150
15
Третья часть числа 450 равна …

50

Ой!
Ошибка!

Верно!
Слайд 16

20
980
147
200
Седьмая часть числа равна 140. Чему равно всё число?

2

Ой!
Ошибка!

Верно!
Слайд 17

МОЛОДЦЫ!
Слайд 18

https://easyen.ru/load/metodika/technologicheski_priem/videourok_sozdanie_prezentacii_s_primeneniem_tekhnologicheskogo_prijoma_universalnyj_trenazhjor/246-1-0-32015 МК «Создание презентации с использованием технологического приёма «Универсальный тренажёр». Автор – Покровкова Н.Н.

https://i.pinimg.com/originals/e6/7f/bf/e67fbf9e30947bdaa25515f1ced4408b.jpg кот Леопольд
Мыши:
http://www.playcast.ru/uploads/2017/07/26/23093132.pnghttp://www.playcast.ru/uploads/2017/12/29/24261721.pnghttps://img1.liveinternet.ru/images/attach/b/4/104/256/104256739large_otr011.pnghttps://img1.liveinternet.ru/images/attach/b/4/104/256/104256861large_otr014.png
https://cf.ppt-online.org/files/slide/n/NomXSCUaT7xy9vlHQ0fRq1JKLnAr5zdIkbeOth/slide-16.jpg кот и мыши

Источники информации

Посмотреть все слайды

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет , так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Публикация «Конспект урока математики во 2 классе „Приёмы умножения нуля и единицы“» размещена в разделах

Математика, 2 класс
Математика. Конспекты уроков
Начальная школа. 1-4 классы
Начальная школа. 2 класс
Школа. Материалы для школьных педагогов
Темочки

Личностные : принимают и осваивают социальную роль обучающегося; имеют мотивацию к учебной деятельности; стремятся развивать внимание, память, логическое мышление, навыки сотрудничества со сверстниками и взрослыми, умение доказывать свою точку зрения,проявляют самостоятельность,личную ответственность. Предметные: понимают суть действия умножения, знают особые случаи умножения,устную и письменную нумерацию чисел в пределах 100, в каких случаях действие сложение можно заменить умножением; отличительные особенности задачи, геометрические фигуры,умеют читать примеры на умножение, решать их,заменяя сложение умножением, заменять суммы, состоящие из одинаковых слагаемых,произведениями; умножать единицу и нуль на число ;решать задачи и выражения изученных видов ; составлять задачи по их кратким записям

Предметные: понимают суть действия умножения, знают особые случаи умножения,устную и письменную нумерацию чисел в пределах 100, в каких случаях действие сложение можно заменить умножением; отличительные особенности задачи, геометрические фигуры,умеют читать примеры на умножение, решать их,заменяя сложение умножением, заменять суммы, состоящие из одинаковых слагаемых,произведениями; умножать единицу и нуль на число ;решать задачи и выражения изученных видов ; составлять задачи по их кратким записям.

Метапредметные : регулятивные: формулируют учебную задачу урока на основе соотнесения того,что известно и усвоено,и того,что еще неизвестно; планируют собственную деятельность и прогнозируют результат,контролируют в форме сличения способа действия и опоры на образец ;оценивают свою деятельность и деятельность партнеров, при необходимости вносят корректировки; способны к саморегуляции ; познавательные : формулируют познавательную цель ; создают алгоритм деятельности ; анализируют, сравнивают, делают выводы; контролируют и оценивают процесс и результаты деятельности; коммуникативные: умеют слушать, слышать и понимать партнеров ; планируют учебное сотрудничество с учителем и со сверстниками ; правильно выражают свои мысли в речи,при необходимости задают вопросы уточняющего характера ; уважают в общении всех участников образовательного процесса.

Оборудование:

1. Маршрутный лист-карта “Океан Математических Знаний”.

2. Макет корабля “Отважный”.

3. Телевизор.

4. Карточка для словарной работы с понятиями “экспедиция, порт, гавань, бухта, пристань”.

5. Толковый словарь В. И. Даля.

6. Детская энциклопедия “Мир животных”.

Умножение в столбик на однозначное число

Чтобы вычислить, к примеру, значение выражения 242 х 2, запишите множители в столбик. Сначала запишите первый множитель:

Далее запишите второй множитель под единицами первого:

Теперь слева поставьте знак умножения «х» и подведите черту внизу:

Начинайте умножать с единиц. При этом можете рассуждать так: 3 единицы умножаем на 2 и получаем 6 единиц. Пишем под единицами 6. 4 десятка умножаем на 2 и получаем 8 десятков. Пишем под десятками 8. 2 сотни умножаем на 2 и получаем 4 сотни. Получаем ответ 486:

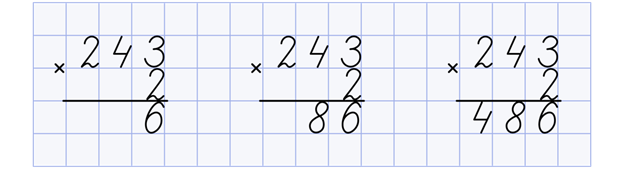
Таким образом, общая схема умножения в столбик на однозначное число будет такова:

Записываете первый множитель.
Записываете второй множитель под единицами первого.
Пишете знак «х» и проводите внизу черту.
Умножаете единицы.
Умножаете десятки.
Умножаете сотни.
Умножаете по порядку следующие разряды.
Получаете ответ.

Иногда при умножении столбиком встречается переход через разряд. Давайте, к примеру, вычислим произведение чисел 3912 и 6.

Здесь пример решается следующим образом:

Пишете первый множитель 3912, а под его единицами пишете второй множитель 6.
Слева ставите знак «х» и проводите внизу черту.
Умножаете 2 единицы на 6 и получаете 12 единиц. В этом числе есть 1 десяток и 2 единицы.
Пишете 2 под единицами и запоминаете 1 десяток, который прибавите к десяткам, которые получите после их умножения. Десяток можно забыть, поэтому напишите 1 над десятками второго множителя.
Умножаете 1 десяток на 6 и получаете 6 десятков. Прибавляете к ним еще 1 десяток, который запомнили, и получаете 7 десятков. Под десятками записываете 7.
Умножаете 9 сотен на 6 и получаете 54 сотни, которые можно представить, как 5 единиц тысяч и 4 сотни.
Пишете 4 под сотнями и запоминаете 5 единиц тысяч, чтобы прибавить их к тысячам, полученным после их умножения. Их можно забыть, поэтому напишите 5 над единицами тысяч первого множителя.
Умножаете 3 тысячи на 6 и получаете 18 тысяч, к которым прибавляете 5 единиц тысяч, которые запомнили, и получаете 23 тысячи.
Записываете все под строкой и получаете ответ 23 472.

Если рассуждать кратко, то алгоритм будет таков:

2 умножить на 6 будет 12. 2 пишете и 1 запоминаете.
1 умножить на 6 будет 6. Прибавляете 1 и получаете 7.
9 умножить на 6 будет 54. Пишете 4 и запоминаете 5.
3 умножить на 6 будет 18. Прибавляете 5 и получаете 23.
Получаете ответ 23 472.

Чтобы было понятнее, что к чему, посмотрите на пример:

В случае, если на однозначное число умножаются числа, которые оканчиваются на один или несколько нулей, запись будет происходить иначе: запищите второй множитель под первой цифрой справа, которая отличается от нуля.

Допустим, вы умножаете 365400 на 3:

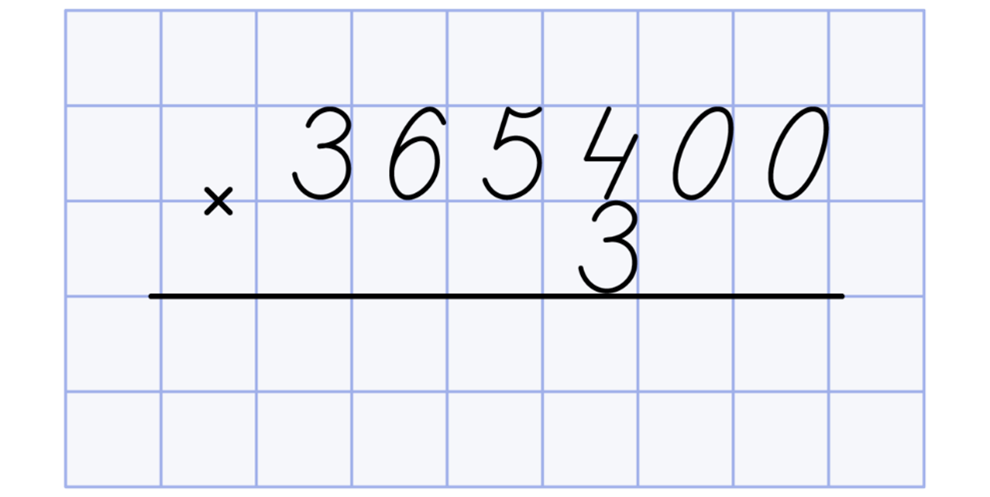
Теперь произведите умножение точно так же, как делали это раньше:

И в конце допишите к результату нули в количестве, оставшемся в первом множителе справа:

Теперь нужно разобраться, как умножать в столбик на двузначное число.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

79*50=(70+9)*50=3500+450=3950
79*7=(70+9)*7=490+63=553
3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

5+4=9
54*11=594

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

7*8=56
5*5=25
75*75=5625

Раньше все считали без калькуляторов

Произведение целых чисел с разными знаками.

Не важен порядок множителей положительное число умножаем на отрицательное или отрицательное число умножаем на положительное, в результате всегда будет отрицательное целое число.

Правило умножения двух целых чисел с разными знаками:При умножении двух целых чисел с разными знаками, их произведение будет равно целому отрицательному числу.

Если упростить определение то, обычно говорят:
“Минус на плюс дает минус”.
“Плюс на минус дает минус”.

Разберем пример:
Вычислить произведение целых чисел.
-4∙6=-24

А теперь докажем правильность этого решения.
-4+(-4)+(-4)+(-4)+(-4)+(-4)=-4∙6=-24
Шесть раз сложили число (-4).

Такой же ответ будет, если поменять местами числа.
6∙(-4)=-24

Пример:
-34∙2=-68

Свойства умножения

Самое главное, что нужно запомнить, следующее:

Если переставить множители местами, произведение не изменится, т.е. a × b = b × a.
Если умножаются три и более множителей, результат их произведения останется неизменным, если любую группу заменить произведением, т.е. a × b × c = (a × b) × c = a × (b × c).
При умножении в столбик с нулями в результате всегда будет получаться ноль, т.е. а × 0 = 0 (а – это любое натуральное число).

При этом в процессе любых вычислений самое главное – это знать таблицу умножения, благодаря чему подсчеты будут быстрыми и упорядоченными. Далее остается только применять алгоритм.

Однозначные и многозначные числа

Для начала введём два новых понятия: однознáчные и многознáчные числа.

Однознáчным называется число, которое состоит из одной цифры. Например, следующие числа являются однознáчными:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Слово «однознáчные» говорит само за себя. Однознáчное — значит состоит из одного знака (цифру иногда называют знáком).

Многознáчным называется число, которое состоит из двух и более цифр. Например, следующие цифры являются многознáчными:

10, 11, 15, 255, 350, 1000, 12500

Многознáчных чисел бесконечно много. Их не сосчитать. Кроме того, они подразделяются на следующие виды:

двузнáчные, которые состоят из двух цифр (например, 25);
трёхзнáчные, которые состоят из трёх цифр (например, 563);
четырёхзнáчные, которые состоят из четырёх цифр (например, 1400)

и так далее, в зависимости от того сколько цифр в числе.

Умножение на 10, 100, 1000

Чтобы умножить любое число на 10, 100 или 1000, достаточно дописáть к множимому количество нулей из множителя.

Например, чтобы умножить 12 на 10, нужно к множимому 12 дописать в конце ноль из множителя 10. В результате получим ответ 120

Еще примеры:

12 × 100 = 1200 (к 12 дописали два нуля, поскольку в числе 100 два нуля)

12 × 1000 = 12000 (к 12 дописали три нуля, поскольку в числе 1000 три нуля)

15 × 100 = 1500 (к 15 дописали два нуля, поскольку в числе 100 два нуля)

320 × 100 = 32000 (к 320 дописали два нуля, поскольку в 100 два нуля)

Если нулём оканчивается не множитель, а множимое, то для получения ответа нужно дописать ноль после множителя.

Например, чтобы умножить 10 на 12, нужно в ответе записать множитель 12 и дописать в конце один ноль:

10 × 12 = 120

Умножение натуральных чисел в столбик

Порядок умножения:

1. Умножить число на число единиц трехзначного числа и получить первое неполное произведение;

2. Умножить число на число десятков трехзначного числа и получить второе неполное произведение (начинать подписывать под десятками);

3. Умножить число на число сотен трехзначного числа и получить третье неполное произведение (начинать подписывать под сотнями);

4. Сложить неполные произведения.

Рассмотрим умножение в столбик умножая на 111

Сначала умножаем единицы; при умножении на десятки дописываем справа к получившемуся произведению, при умножении на сотни — 00 и т.д. Затем складываем получившиеся числа.

Рассмотрим более сложный пример

Объяснение примера умножения в столбик:

1. Умножаем число 397 на 3 единицы второго множителя, получаем первое неполное произведение 1 191;

2. Умножаем 397 на 2 десятка второго множителя. Получаем второе неполное произведение 794;

3. Умножаем 397 на 2 сотни второго множителя. Получаем третье неполное произведение 794;

4. Складываем неполные произведения 1 191, 794 и 794, получаем 88 531.

Умножение многозначных чисел на многозначные

Умножение многозначных чисел на многозначные происходит таким же образом, как и умножение многозначных на однозначные. Каждая цифра многозначного числа умножается на каждую цифру другого многозначного числа. Единственное отличие заключается в том, что в конце образуется своего рода лесенка ответов, которые надо сложить. Рассмотрим несколько примеров, чтобы хорошо понять это.

Пример 1. Найти значение выражения 12 × 14

Записываем данное выражение в столбик — единицы под единицами, десятки десятками:

Теперь умножаем каждую цифру числа 12 на каждую цифру числа 14. Делать это надо по-очереди, начав с четвёрки. В результате таких действий мы приходим к умножению многозначного числа на однозначное, которое проходили ранее:

Умножив 12 на 4, мы получили число 48, которое записали таким образом, чтобы разряд единиц этого числа оказался под четверкой, на которую мы умножали число 12.

Теперь умножаем 12 на 1:

Умножив 12 на 1 мы получили число 12 и записали его таким образом, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножали число 12.

Мы получили лесенку ответов 48 и 12, которую надо сложить. Складываем и получаем ответ 168

В данном примере множитель 14 это четыре единицы и один десяток. Тогда умножение 12 на 14 можно понимать как увеличение числа 12 в четыре раза и в десять раз. Этим и объясняется появление лесенки в конце решения. Давайте посмотрим как это выглядит на каждом этапе:

Увеличим число 12 в четыре раза, получим число 48

Увеличим число 12 в десять раз, получим число 120. Записываем 120 так, чтобы можно было сложить единицы этого числа с единицами числа 48, а десятки числа 120 можно было сложить с десятками числа 48

Теперь сложим получившуюся лесенку ответов. Единицы сложим с единицами, десятки с десятками, сотни с сотнями. В результате образуется окончательный ответ:

Но чаще всего множитель не группируется с помощью разрядов, и умножение выполняют, умножая каждую цифру множимого на каждую цифру множителя.

Пример 2. Найти значение выражения 25 × 36

Записываем данное выражение в столбик

Умножаем каждую цифру числа 25 на каждую цифру числа 36.

Умножим 25 на 6:

Умножаем 25 на 3:

Теперь сложим получившуюся лесенку:

Получили ответ 900.

Рассмотрим большой и сложный пример на умножение: 12305 × 5641. Будем придерживаться ранее изученных правил.

Сначала записываем в столбик данное выражение

Теперь начинаем умножать. Число 12305 надо умножить на каждую цифру числа 5641.

Умножив 12305 на 1, мы получили 12305 и записали это число так, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножили 12305.

Теперь умножаем 12305 на следующую цифру 4:

Умножив 12305 на 4, мы получили 49220 и записали это число так, чтобы разряд единиц этого числа оказался под четверкой, на которую умножали 12305.

Умножаем 12305 на следующую цифру 6:

Умножив 12305 на 6, мы получили 73830 и записали это число так, чтобы разряд единиц этого числа оказался под шестёркой, на которую мы умножали 12305.

Теперь умножаем 12305 на последнюю цифру 5:

Умножив 12305 на 5, мы получили 61525 и записали это число так, чтобы разряд единиц этого числа оказался под пятёркой, на которую умножали 12305.

В результате мы получили большую лесенку, которую надо сложить. Складываем:

Получили окончательный ответ 69412505.

Если вы поняли этот пример, то можно сказать, что умножение больших чисел вы усвоили на отлично.

На этом урок по умножению можно завершить. Обязательно потренируйтесь, решив несколько примеров, которые даны ниже.

Важно отметить, что все эти стрелки и подробные решения, как на картинках в «боевых условиях» рисовать не принято. Нужно уметь сразу записывать ответы, выполняя в уме все вычисления

Исключением является то, если человек давно не занимался математикой или никогда ею не занимался. В таком случае можно рисовать для себя стрелки и другие вспомогательные схемы для хорошего усвоения материала.

Правило произведения целых чисел.

Определение:Произведением двух целых чисел не равных нулю называют произведение их модулей и результат будет со знаком плюс, если эти числа одинаковых знаков, и со знаком минус, если они разных знаков.

Самое главное в произведении целых чисел это правильно посчитать знак ответа. Например, оба множителя могут быть положительными или оба отрицательными числами, или один множитель положительный, а другой отрицательный.

Нужно запомнить:

Плюс на плюс дает плюс.“+ ∙ + = +”

Минус на минус дает плюс.“– ∙ – =+”

Минус на плюс дает минус.“– ∙ + = –”

Плюс на минус дает минус.“+ ∙ – = –”

Каждый случай ниже разберем подробно.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Зачем уметь умножать в столбик?

Умножение столбиком – это метод умножения чисел, в котором числа разбиваются на столбцы, выполняются отдельные умножения каждого столбца, а затем складываются результаты.

Обычно этот метод преподается школьникам в качестве метода простого умножения больших чисел и часто используется в образовательных целях для укрепления основ арифметики.

Однако эта техника также используется людьми, которые предпочитают выполнять вычисления вручную, например, бухгалтерами, финансистами и прочими специалистами, чья деятельность связана с вычислениями.

Кроме того, умножение столбиком может быть полезным инструментом для проверки точности вычислений, выполненных другим человеком или даже компьютером или калькулятором.

Метод прост в понимании и выполнении, что делает его полезным для людей всех возрастов и уровней образования.

Алгоритм умножения в столбик

Освоить умножение в столбик очень просто – для этого нужно лишь запомнить несколько шагов, а именно:

Запишите пример в строку, а затем найдите и подчеркните наименьшее из двух чисел. После записи в столбик это число должно стоять снизу.
Запишите произведение в виде столбика. Первым записывайте больший множитель, а вторым – меньший (тот, который вы подчеркнули на предыдущем шаге). Слева от множителей поставьте знак умножения «х» и проведите черту, по которой будете записывать решение

Обращайте особое внимание на разряды: единицы должны стоять под единицами, десятки – под десятками и т.д.
По порядку выполните нужные действия: каждая цифра первого множителя должна быть умножена на крайнюю цифру второго. Расчеты производите справа налево, т.е

сначала единицы, потом десятки, потом сотни. В случае, если результат получается двузначным, запишите под чертой только его последнюю цифру, а остальное перенесите в следующий разряд, складывая его с тем, что получите при следующем умножении.
Когда умножите на единицу второй множитель, выполните те же самые операции с остальными цифрами. Запишите результаты под чертой, сдвигаясь на одну позицию влево.
Сложите то, что получилось, и запишите ответ.

Чтобы алгоритм был более понятен, посмотрите на следующий пример:

Теперь можно переходить к разным вариантам умножения.

Умножение или произведение нескольких целых чисел.

Чтобы посчитать произведение нескольких целых чисел, нужно умножать числа по парно или последовательно, например:
(-3) ∙5∙(-11) ∙(-9) ∙1=((-3) ∙5)∙((-11) ∙(-9)) ∙1=((-15) ∙99) ∙1=(-1485) ∙1=-1485

Сначала сгруппировали по два числа ((-3) ∙5) и ((-11) ∙(-9)), потом ((-15) ∙99) и нашли ответ.

При перемножении целых чисел, результат всегда будет целым числом.

Вопросы по теме:Как влияет при умножении на целое число (-1)?
Ответ: так как (-1) отрицательное число, при умножении на целое число происходит смена знака числа.
Пример: (-1) ∙3=-3 . Число 3 было со знаком “+”, а стало со знаком “–”.
Еще пример: (-1) ∙(-5)=5 . Число (-5) было со знаком “–”, а стало со знаком “+”.

Пример №1:
Найти произведение двух целых чисел: а) (-2) ∙235 б) (-34) ∙(-17) в) 1∙(-12) г) 0∙4983

Решение:
а) (-2) ∙235=-470
б) (-34) ∙(-17)=578
в) 1∙(-12)=-12
г) 0∙4983=0

Пример №2:
Чему равно произведение последовательных целых чисел, начинающихся числом -100 и оканчивающихся числом 100?

Решение:
Между числами -100 и 100 находится нуль, а любое число, умноженное на 0 равно 0. Поэтому произведение последовательных целых чисел от -100 до 100 равно 0.
Ответ: 0.

Пример №3:
Чему равно произведение всех целых чисел?

Решение:
Целые числа состоят из целых положительных и отрицательных чисел, а также нуля. При умножении любого числа на нуль будет 0. Поэтому произведение всех целых чисел равно 0.
Ответ: 0.