Запись и чтение чисел второго десятка
Медведь ушел в огород, а Маша осталась в доме.
— Мишка! Мишка! – вскоре раздался ее крик.
— Что случилось? – спросил Медведь, забежав в дом.
— Я пишу письмо Зайке, чтобы рассказать о новых числах, которые мы выучили – ответила Маша, — но не знаю, как их написать.
— Хорошо, я расскажу тебе о письменной нумерации чисел 11 – 20– сказал Медведь и принялся объяснять.
— Множество конфет, которые мы пересчитывали, состояло из двух частей – коробки, в которой было десять конфет (а это один десяток) и отдельных конфеток. Поэтому, чтобы записать эти числа нам нужно использовать две цифры. Такие числа называют двузначными.
Первая цифра должна показывать, сколько в нашем множестве десятков.
Вторая цифра обозначает количество отдельных конфет.
В математике количество целых десятков записывается в разряд десятков, а количество отдельных элементов в разряд единиц. У чисел второго десятка всего два разряда.
| Десятки | Единицы |
— Давай покажу тебе это на примере твоих конфет – сказал Медведь.
— А я их уже съела, — ответила Маша – остались только палочки от леденцов.
— Хорошо, подойдут и палочки, — проворчал Мишка – только неси все палочки, которые у тебя есть.
Маша принесла палочки, и Медведь продолжил объяснения.
— Сначала отсчитаем десять палочек.
— Свяжем их в пучок. Теперь это целый десяток.
— Сколько ты видишь десятков? – спросил Мишка.
— Я вижу один такой пучок – ответила Маша.
— Правильно, у нас один десяток. А сколько отдельных палочек?
— Я их не вижу, отдельных палочек нет.
— Смотри, как надо записать это в нашу таблицу.
— У нас получилось число 10. Это наименьшее двузначное число. Ты его уже знаешь.
— Давай продолжим и положим еще одну палочку. Что ты видишь теперь?
— Я вижу один целый пучок и одну отдельную палочку.
— Верно. Раз отдельная палочка одна, то число называется одиннадцать. А в таблицу мы в разряд десятков пишем, что пучок 1 и в разряд единиц пишем, что палочка 1.
— Добавим еще одну палочку. Что получим теперь?
— Теперь у нас один десяток и две отдельные палочки. Я знаю, раз палочек только две, то это число двенадцать – обрадовалась Маша.
— Все верно. Смотри, как это надо записать.
— Обрати внимание! Когда мы называем число «двенадцать» — мы сначала называем сколько отдельных элементов – «два». А когда записываем это число цифрами, то сначала указываем количество десятков и только потом, количество отдельных единиц.
— Я все поняла – обрадовалась Маша.
— Тогда сама запиши следующее число – попросил Медведь.
— Я вижу три отдельные палочки и десяток – значит, это число тринадцать. В таблицу я запишу, что здесь 1 десяток и 3 единицы.
— Молодец, ты все правильно сделала. Запиши самостоятельно все остальные числа, чтобы закончить таблицу нумерации чисел от 11 до 20.
Вот что у Маши получилось.
Потом Маша положила еще одну палочку и у нее получилось 10 отдельных палочек.
— Мишка! – позвала Маша. – Что мне теперь делать?
Медведь посмотрел и сказал.
— У тебя получилось десять отдельных палочек – теперь их тоже нужно связать в целый пучок.
— Что ты видишь?
— У нас два десятка, а отдельных палочек нет. Это число двадцать. Как его записать? – спросила Маша.
— Так же, как и остальные – в разряд десятков запишем, что их 2, а в разряд единиц запишем 0, потому что у нас нет отдельных единиц.
— Теперь давай проверим, сможешь ли ты самостоятельно сделать запись чисел второго десятка – сказал Медведь. – Я буду называть количество десятков и единиц в числе, а ты скажешь, что это за число. Например, 1 десяток и 3 единицы.
— Это число тринадцать.
— Правильно.
— Ура! Я теперь знаю, как можно записать все числа от 10 до 20. Это двузначные числа, у которых сразу записываем количество десятков, а потом количество единиц – обрадовалась Маша.
— Правильно. Скоро ты познакомишься с остальными двузначными числами, а пока тренируйся называть, записывать и показывать числа от 11 до 20 – похвалил ее Мишка.
Название и образование чисел от 11 до 20
Всем известно, что Маша большая сладкоежка. Медведь решил порадовать ее и купил для нее целый пакет конфет.
Но пока он нес подарок домой, пакет порвался и конфеты стали понемногу высыпаться. Зашел Медведь в дом, позвал Машу и отдал ей угощение.
Развернула Маша пакет, а там только коробка с конфетами лежит. Открыла она коробку и начала считать: «Один, два, три, четыре, пять, шесть, семь, восемь, девять, десять». Всего десять конфет оказалось в коробке.
— Мишка! – закричала Маша. – Почему ты принес так мало конфет?!
Маша обиделась и чуть не заплакала.
Прибежал Медведь. Заглянул в пакет. И схватился за голову. Понял он, что половину конфет растерял по дороге. Рассказал Медведь Маше, что конфет было больше, только они рассыпались и куда-то закатились.
Обрадовалась Маша и бросилась искать конфеты. Первую конфету она нашла тут же под столом и положила ее рядом с коробкой.
— Мишка! – позвала Маша. – Я нашла конфету! Иди сюда, посмотри!
Пришел Медведь, глянул на стол и сказал: «Теперь у тебя одиннадцать конфет!»
— Сколько, сколько? – переспросила Маша.
— Одиннадцать! – ответил Медведь.
— Первый раз слышу такое слово. Что оно обозначает? – удивилась Маша.
— Ну, смотри, — сказал Мишка, — у тебя в коробке было десять конфет. Десять – это десяток. В старину вместо слова «десяток» говорили «дцать».
— Дцать! Дцать! – засмеялась Маша. – Какое смешное слово!
— А теперь у тебя есть еще одна – Мишка положил конфету на коробку. – Получается «один на дцать» или целое слово «одиннадцать».
— Одиннадцать – повторила Маша. – Поняла, это если у меня есть десять или десяток и еще один.
Маша принялась искать остальные конфеты. Она обшарила всю комнату.
Под диваном она нашла еще одну конфету и положила ее на стол.
— Мишка! – позвала Маша, — я нашла еще одну конфету. Иди, посмотри, сколько их теперь.
Медведь подошел к столу и сказал: «Теперь здесь двенадцать конфет».
— Двенадцать, две-на-дцать – проговорила Маша.
— Ну да – сказал Медведь. — Вот смотри – десяток в коробке и еще две конфеты. Что получим?
— Поняла – десять и еще два – это число двенадцать. Очень интересно. Сейчас поищу еще конфеты – сказала Маша.
Она принялась оглядываться по сторонам и в углу за умывальником обнаружила конфетку.
— Мишка! Я нашла третью конфету! Иди, посчитай, сколько их теперь – закричала Маша.
Медведь увидел на столе возле коробки с шоколадками еще три конфеты.
— Давай вместе разберемся – сказал Мишка. – Ты нашла уже три конфеты, а в коробке десять или десяток, который называли «дцать». Значит всего их тринадцать.
— Так значит нужно посчитать, сколько у меня отдельных конфет. От этого зависит название всего числа – поняла Маша. – Сейчас я сама попробую разобраться.
Она бросилась искать по комнате остальные конфеты. И нашла еще парочку.
— Посмотрим, что у меня получится – сказала Маша и положила возле коробки еще одну конфету. – Теперь у меня четыре конфеты, кроме тех, что в коробке.
— Как там говорил Мишка? – вспоминала Маша. – Четыре – на – дцать.
— Мишка! У меня теперь четыренадцать конфет! – закричала она.
— Четырнадцать – поправил ее Мишка, — надо говорить «четырнадцать». Но посчитала ты все правильно, молодец.
Маша положила рядом еще конфету.
— Смотри, Мишка, теперь возле коробки лежит пять конфет – сказала Маша, — значит всего конфет пять – на – дцать. Правильно?
— Пятнадцать! Молодец, ты все правильно поняла – похвалил медведь Машу.
Обрадовалась Маша и побежала во двор искать остальные конфеты.
Она нашла еще несколько конфет.
Принесла их домой. Маша начала выкладывать на стол по одной конфете и пересчитывать то, что получалось. Вот какие числа она узнала.
— Мишка! – закричала Маша. – Иди быстрее сюда! Послушай, какие числа у меня получились: шестнадцать, семнадцать, восемнадцать, девятнадцать. Правильно?
— Все верно – сказал Медведь. – Ты молодец! Вот тебе еще одна конфета.
Мишка положил на стол шоколадку.
Маша принялась пересчитывать конфеты на столе. У нее получилось десять.
— А сколько теперь всего конфет? – спросила Маша. – В коробке десять и на столе десять.
— Я уже говорил, что десять – это десяток – сказал Мишка. — Смотри, что получилось. В коробке один десяток и на столе один десяток конфет.
— Получается, у нас два десятка – сказала Маша.
— Правильно, — ответил Мишка. – Раз два десятка, то число называется «двадцать».
— Два –дцать – все понятно, это легко запомнить – обрадовалась Маша. – Я теперь знаю названия всех чисел от 11 до 20! Какая я молодец!
Маша принялась есть конфеты, а Медведь смотрел на нее и улыбался. Он был рад, что Маша поняла принцип образования чисел от 11 до 20.
Числа от 1 до 1000 Умножение на числа, оканчивающиеся нулямиПисьменное умножение двух чисел, оканчивающихся нулямиОтветы к стр. 16
Учимся решать задачи: выполнять схематические чертежи, сравнивать задачи и их решения.
61. Реши задачи, сравни решения.1) Два лыжника вышли одновременно навстречу друг другу из двух поселков и встретились через 3 ч. Первый лыжник шел со скоростью 12 км/ч, а второй − со скоростью 14 км/ч. Найди расстояние между поселками.

2) Из двух поселков, расстояние между которыми 78 км, вышли одновременно навстречу друг другу два лыжника. Первый из них шел со скоростью 12 км/ч, а второй со скоростью 14 км/ч. Через сколько часов лыжники встретились?

3) Из двух поселков, находящихся на расстоянии 78 км, вышли одновременно навстречу друг другу два лыжника и встретились через 3 ч. Первый лыжник шел со скоростью 12 км/ч. С какой скоростью шел второй лыжник?

1-я задача
1) 12 • 3 = 36 (км) − прошел первый лыжник
2) 14 • 3 = 42 (км) − прошел второй лыжник
3) 36 + 42 = 78 (км)
О т в е т: расстояние между поселками 78 км.
2-я задача
1) 12 + 14 = 26 (км/ч) − скорость сближения лыжников
2) 78 26 = 3 (ч)
О т в е т: время лыжников в пути до встречи 3 часа.
3-я задача
1) 78 3 = 26 (км/ч) − скорость сближения лыжников
2) 26 − 14 = 14 (км/ч)
О т в е т: скорость второго лыжника 14 км/ч.
В первом случае мы искали расстояние между поселками, умножив скорости лыжников на время в пути до встречи и сложив результаты. Во втором — время лыжников до встречи, сложив скорости лыжников и разделив расстояние между поселками на этот результат. А в третьем — скорость второго лыжника, разделив расстояние между городами на время в пути и отняв от этого результат скорость первого лыжника.
62. Составь и реши три похожие задачи про пешеходов, которые шли навстречу друг другу со скоростями 4 км/ч и 5 км/ч и встретились через 2 ч.
1-я задача.
Два пешехода вышли одновременно навстречу друг другу из двух поселков и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч, а второй − со скоростью 5 км/ч. Найди расстояние между поселками.
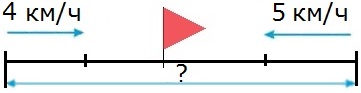
1) 4 • 2 = 8 (км) − прошел первый пешеход
2) 5 • 2 = 10 (км) − прошел второй пешеход
3) 8 + 10 = 18 (км)
О т в е т: расстояние между поселками 18 км.
2-я задача.
Из двух поселков, расстояние между которыми 18 км, вышли одновременно навстречу друг другу два пешехода. Первый из них шел со скоростью 4 км/ч, а второй со скоростью 5 км/ч. Через сколько часов пешеходы встретились?
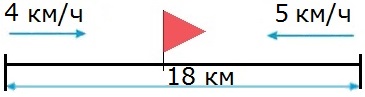
1) 4 + 5 = 9 (км/ч) − скорость сближения пешеходов
2) 18 9 = 2 (ч)
О т в е т: пешеходы встретились через 2 часа.
3-я задача
Из двух поселков, находящихся на расстоянии 18 км, вышли одновременно навстречу друг другу два пешехода и встретились через 2 ч. Первый пешеход шел со скоростью 4 км/ч. С какой скоростью шел второй пешеход?
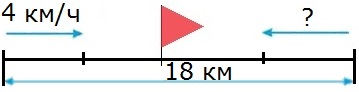
1) 18 2 = 9 (км/ч) − скорость сближения пешеходов
2) 9 − 4 = 5 (км/ч)
О т в е т: скорость второго пешехода 5 км/ч.
63. (Устно.) 600 : 3 + 7 • 5 40 • (16 − ![]() • 2 600 : (3 + 7) • 5 40 • (16 − 8 • 2)
• 2 600 : (3 + 7) • 5 40 • (16 − 8 • 2)
600 3 + 7 • 5 = 200 + 35 = 235
600 (3 + 7) • 5 = 600 10 • 5 = 60 • 5 = 300
40 • (16 − ![]() • 2 = 40 • 8 • 2 = 320 • 2 = 640
• 2 = 40 • 8 • 2 = 320 • 2 = 640
40 • (16 − 8 • 2) = 40 • (16 − 16) = 40 • 0 = 0
64. 8070 • 600 5010 − 15900 : 100 + 786
×8070 600 4842000
5010 − 15900 100 + 786 = 5010 − 159 + 786 = 4851 + 786 = 5637_ 5010 +4851 159 786 4851 5637
9800 • 30 30200 − 7020 : 10 • 3 + 68
×9800 30 294000
30200 − 7020 10 • 3 + 68 = 30200 — 702 • 3 + 68 = 28094 + 68 = 28162×702 +30200 3 2106
2106 28094
ЗАДАНИЕ НА ПОЛЯХЦЕПОЧКА
| ← Предыдущая | Следующая → |
Страница 17
Задание 1.
- 1) Запиши и прочитай число, которое состоит из 2 дес. и 8 ед.; 6 дес; 9 дес; 10 дес; 4 дес.
- 2) Под каждым из этих чисел запиши число, которое на 20 меньше его.
- 1) 28, двадцать восемь; 60, шестьдесят; 90, девяносто; 100 сто; 40 сорок.
- 2) 8, 40, 70, 80, 20.
Задание 2.
У Саши было 10 р., а у Вани — 20 р. Поставь вопрос так, чтобы задача решалась сложением. Измени вопрос, чтобы задача решалась вычитанием. Реши эти задачи.
- 1) Сколько рублей у Саши и у Вани вместе?
- 1) 10 + 20 = 30 (р).
- Ответ: у Саши и у Вани вместе 30 рублей.
- 2) На сколько рублей больше у Ваши, чем у Саши?
- 1) 20 — 10 = 10 (р).
- Ответ: у Вани на 10 р. больше.
Задание 3.
Как можно набрать такими монетами 16 к.? 27 к.? 51 к.? 56 к.? 65 к.? 70 к.?
- 1) 16 к. = 10 к. + 5 к. + 1 к.;
- 2) 27 к. = 10 к. + 10 к. + 5 к. + 1 к. + 1 к.;
- 3) 51 к. = 50 к. + 1 к.;
- 4) 56 к. = 50 к. + 5 к. + 1 к.;
- 5) 65 к. = 50 к. + 10 к. + 5 к.;
- 6) 70 к. = 50 к. + 10 к. + 10 к..
Задание 4.
Оля перепрыгнула через верёвочку 18 раз, а Света — только 10 раз. Поставь вопрос и реши задачу.
Сколько раз перепрыгнули через верёвочку Оля и Света вместе?
- 1) 18 + 10 = 28 (раз).
- Ответ: 28 раз.
Задание 5.
Мальчики прыгали в длину с места. Кто из них занял первое, второе и третье места, если длина прыжка Васи была равна 85 см, Вити — 91 см, а Юры — 9 дм?
9 дм = 90 см. Витя занял 1 место, Юра второе, Вася третье место.
Задание 6.
Вася выше Саши на 8 см, а Коля ниже Саши на 3 см. Кто из мальчиков самый высокий? На сколько сантиметров самый высокий из мальчиков выше самого маленького?
- 1) 8 + 3 = 11 (см).
- Ответ: Вася самый высокий, Коля самый маленький, Вася выше Коли на 11 см.
Запиши, сколько копеек содержится в 1 р.
Узнай, на сколько копеек 1 р. больше, чем 1 к.
10 + 6 = 16
Потом Мишка начал рассказывать, как можно легко выполнить вычитание из чисел второго десятка разрядное число.
— Давай вспомним о множестве, которое обозначает число 16.
Если из этого множества убрать одно из подмножеств, то останется другое подмножество.
Мы из числа 16 убрали все элементы разряда десятков. Значит останутся только элементы разряда единиц. Математическая запись выглядит так: 16 – 10 = 6.
А теперь из множества числа 16 уберем все элементы разряда единиц и останутся только элементы разряда десятков.
Записывается это так: 16 – 6 = 10.
— Это очень легко – сказала Маша – даже считать ничего не надо или таблицы учить.
— Верно – ответил Мишка. –Ты можешь легко решить пример, в котором вычитаемое является разрядным числом. Для этого нужно уменьшаемое представить в виде суммы разрядных слагаемых и убрать соответствующие элементы одного из разрядов.
— Потренируйся самостоятельно решить примеры:
— Ты со всем справилась – похвалили Медведь Машу. – А теперь пойдем пить чай – у меня для тебя есть еще несколько вкусных конфет.
Маша с радостью согласилась.
Вот и закончился наш мультфильм. Надеюсь, ты вместе с Машей запомнил, как образуются числа в пределах 11 – 20, освоил запись и чтение чисел второго десятка и научился решать примеры, в которых компоненты являются разрядными числами. Чтобы проверить, как ты усвоил этот материал, выполни тестовые задания.
Страница 18. Странички для любознательных.
Задание 1.
В лесной школе 14 учеников: ежи, зайцы и белки. Меньше всего в школе ежей, а больше всего зайцев: их на 5 больше, чем ежей. Сколько в лесной школе зайцев, белок и ежей?
Решение:
- Если от 14 отнять 5, получим число, в котором будет равное количество ежей и зайцев. 1) 14 — 5 = 9
- Так, как белок больше, чем ежей, значит их не может быть поровну то есть по 3. Ежей меньше всего, а белок меньше, чем зайцев, значит ежей 2.2) 2 + 5 = 7 (зайцев)
- 3) 7 + 2 = 9 (зверей) ежей и зайцев;
- 4) 14 — 9 = 5 (белок).
- Ответ: ежей 2, зайцев 7, белок 5.
Задание 2.
В лесной школе 2 белки соревновались с 2 ежами в умении решать задачи. Всего участники соревнования решили 11 задач, причём все — разное количество. Кто решил больше задач: белки или ежи, если один ёж решил больше всех, а другой — меньше всех?
Страинца: —>> 16 — 18 19 — 21 22 — 24
Сложение и вычитание вида 10+6, 16-6, 16-10
Вечером Медведь, окончив все свои дела, вошел в дом и сел отдохнуть. Маша стала его просить, чтобы он рассказал ей еще что-то интересное о числах. Мишка согласился, но сначала предложил ей поиграть в игру.
Медведь называл числа, а Маша показывала их с помощью палочек.
— Покажи число шестнадцать – попросил Мишка.
— Это легко – ответила Маша. — Число записывается так – 16. Значит в нем 1 десяток и 6 единиц.
Маша положила на стол палочки.
— Правильно — сказал Мишка. – Один десяток мы обозначим числом 10, а шесть единиц – числом 6. Множество палочек, которое мы обозначаем числом 16, состоит из двух подмножеств в которых 10 и 6 элементов.
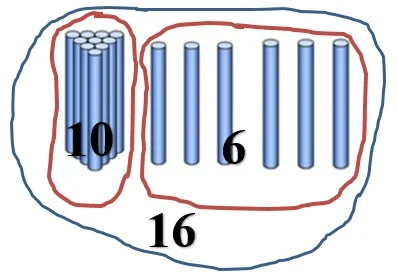
В математике это записывается так: 16 = 10 + 6. Это называется представление числа в виде суммы разрядных слагаемых.
Слагаемое 10 показывает, сколько всего элементов в разряде десятков. В числе 16 – 1 десяток, а 1 десяток это 10 единиц.
Слагаемое 6 показывает, сколько всего элементов в разряде единиц.
Числа 10 и 6 в данном случае называются разрядными числами.
Мишка предложил Маше и другие числа от 11 до 20 представить в виде суммы разрядных слагаемых.
Вот что у нее получилось.






























