Квадратичная функция. парабола

Промежутки знакопостоянства и корни функции

Числовые промежутки, на которых функция сохраняет свой знак (то есть остается положительной или отрицательной), называются промежутками знакопостоянства функции.

О промежутках знакопостоянства функции можно сделать вывод, посмотрев на график функции. Например, возьмем график функции . Здесь при , при . В первом случае график расположен выше оси , во втором – ниже ее.

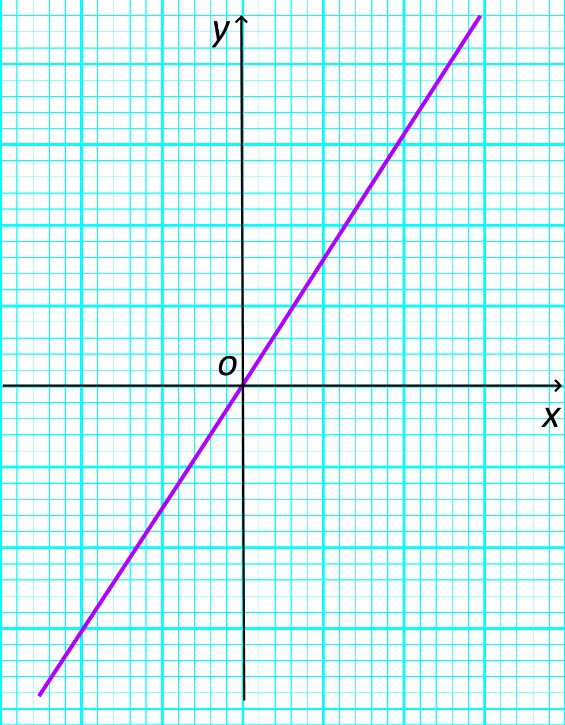
График линейной функции

Значения аргумента , при которых , называются корнями (или нулями) функции. Значения аргумента, при которых функция обращается в нуль – это абсциссы точек пересечения графика функции с осью : ,  ,  .

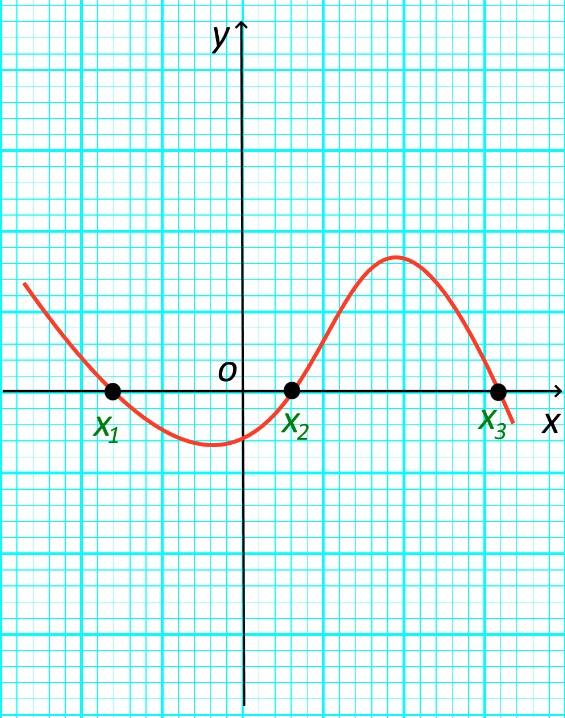
Корни функции

Итак, мы с вами изучили что такое функция, определили когда функция является четной, а когда нечетной, способы задания функции, область определения функции и область ее значений. А также дали понятие периодической функции и корней функции. Выяснили, что называется промежутками знакопостоянства функции. Привели примеры.

Как найти область определения функции

Для того, чтобы найти область определения функции, мы должны определить – где функция будет существовать, при каких значениях аргумента. Приведем примеры:

Пример 1

Найти область определения функции 

Зададимся вопросом – при каких значениях функция будет существовать? Очевидно, что функция существует, если знаменатель дроби не равен нулю. То есть .

Для определения этого значения решим уравнение:

.

Находим, .

То есть функция не будет существовать при значении . Тогда областью определения функции (где она существует) – будут все значения кроме 5. Через интервалы можно записать так:

Пример 2

Найти область определения функции .

Здесь функция определена при любых значениях аргумента. То есть D(f) – все числа.

Пример 3

Определить область определения функции

.

Выражение, стоящее под знаком квадратного корня, должно быть больше или равно нулю. Таким образом, мы можем записать:

Решим данное неравенство и получим: .

Тогда область определения функции будет интервал значений аргумента .

Способы задания функции

Функция может быть задана аналитически в виде формулы , где переменная – элемент множества значений аргумента, а переменная – соответствующее значение функции.

Например, формула определяет некоторую функцию, где каждому значению переменной , взятому из области определения функции, соответствует единственное значение переменной .

Функция   полностью определяется заданием множества пар ,  где принимает все значения из , а – соответствующие значения функции.

Однако не всякое множество точек координатной плоскости является графиком некоторой функции. Например, если мы рассмотрим следующий график, то увидим, что значению соответствуют три значения , и, следовательно, такое соответствие не является функцией.

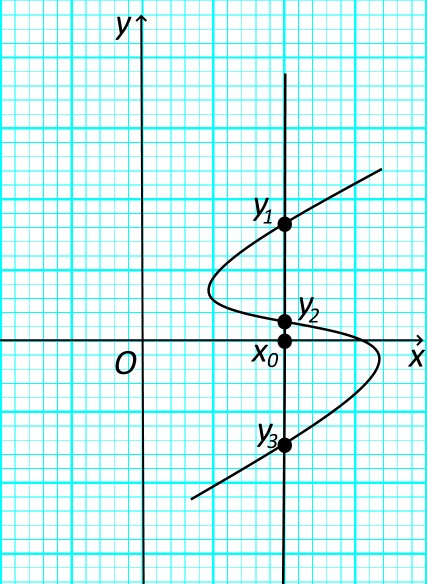
График не является графиком функции

Для того, чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси , пересекалась с указанным графиком не более чем в одной точке.

Четные и нечетные функции

Функция называется четной, если она обладает следующими двумя свойствами:

1. Область определения этой функции симметрична относительно точки О (то есть, если точка принадлежит области определения, то точка также принадлежит области определения).
2. Для любого значения , принадлежащего области определения этой функции, выполняется равенство .

График четной функции – пример.

Функция называется нечетной, если:

1. Область определения этой функции симметрична относительно точки O.
2. Для любого значения , принадлежащего области определения этой функции, выполняется равенство .

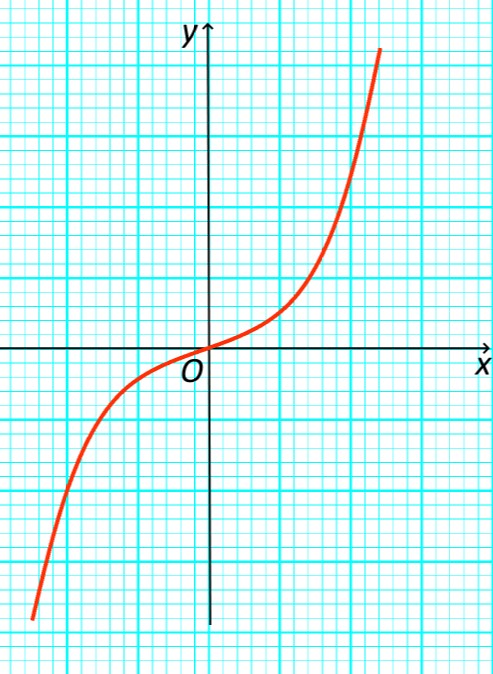
График нечетной функции – пример.

Заметим, что не всякая функция является четной или нечетной. Например, каждая из функций и   не является ни четной, ни нечетной.

Пример 1

Доказать, что функция не является ни четной, ни нечетной.

Доказательство.

Областью определения данной функции является вся числовая прямая, то есть условие 1 выполнено. Проверяем условие 2.

Чтобы доказать, что функция не является четной, нам нужно доказать, что условие 2 для четной функции не выполняется, то есть что .

Пусть , тогда . Проверяем:

Пример 2

Определите четность или нечетность функции:

Решение: область определения данной функции – вся числовая ось, кроме точки (на ноль делить нельзя).  Найдем .

Получим: . Вынесем минус за скобки:

Отсюда выходит, что , то есть выполняется условие для нечетной функции. А, значит, функция – нечетная функция.

Пример 3

Определить четность или нечетность функции:

Решение: Первое условие о симметричности области определения функции выполняется, так как область определения функции . Переменим знак аргумента функции и упростим:

Получается, что . То есть функция

Монотонность функции

Функция называется возрастающей на данном числовом промежутке , если большему значению аргумента соответствует большее значение функции . Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .

Функция называется убывающей на данном числовом промежутке , если большему значению аргумента соответствует меньшее значение функции . Это значит, что для любых и из промежутка , таких, что , выполнено неравенство .

Функция только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.

О монотонности функции можно судить по ее графику. Например, функция, график которой изображен ниже является монотонно возрастающей на всей числовой оси.

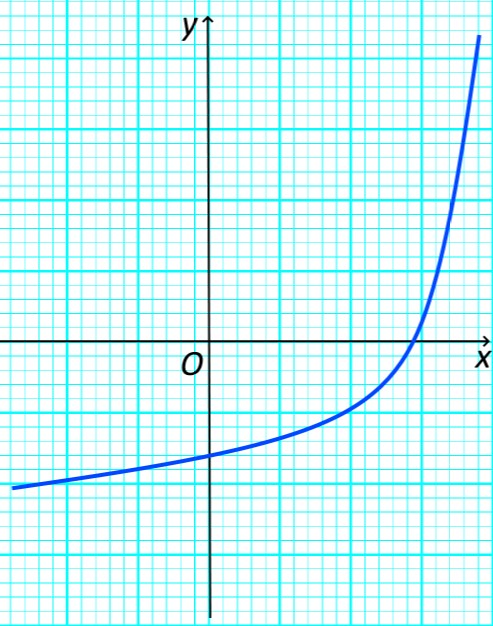
Монотонно возрастающая функция

А вот эта функция является монотонно убывающей.

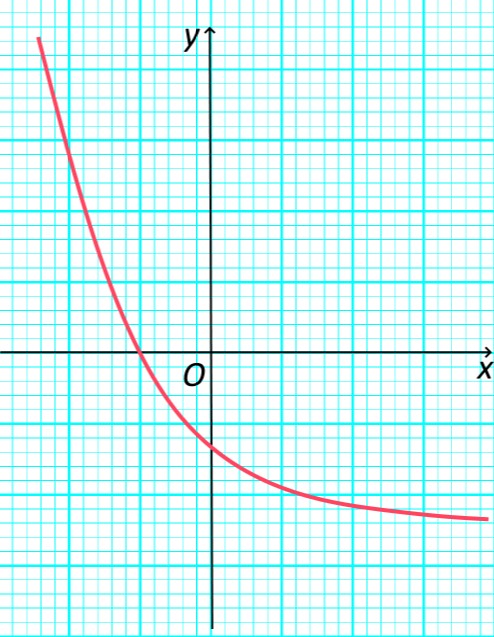
Монотонно убывающая функция – график функции.

А теперь рассмотрим вот такой график функции – на ней функция убывает на промежутке и возрастает на промежутке .

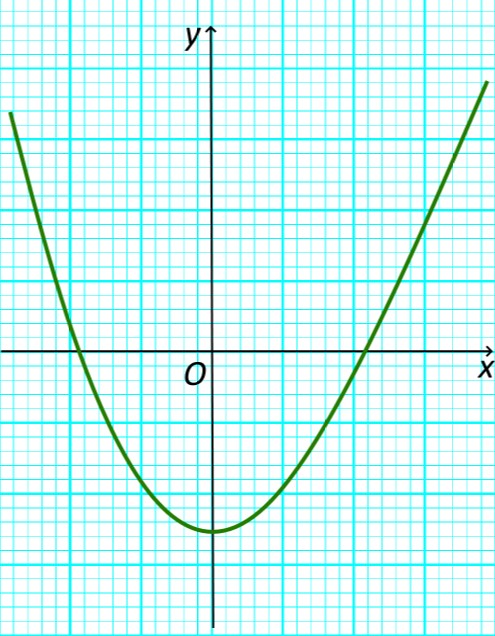
График функции которая монотонно убывает и монотонно возрастает на определенных интервалах области определения функции.

Пример

Докажите, что функция, заданная формулой , где , возрастающая.

Решение: Пусть , где и . Тогда

Поскольку , то и , а, значит, 

Область определения и область значений функции

Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции приняты обозначения: –  область определения функции, – множество значений функции.

– значение функции в точке .

Если область определения функции и область ее значений определены в множестве рациональных чисел, то функцию называют числовой.

Элементы множества еще называют значениями аргумента, а соответствующие им элементы – значениями функции.

Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

Например, область определения функции, заданной формулой , состоит из всех чисел, кроме нуля.