Как именно стоит использовать ГДЗ
Списывание, конечно, не порок, но именно при изучении алгебры — это большая ошибка. Школьникам необходимо разобраться в сути формул и алгоритмов, а просто «скатав» материал, сделать это невозможно. При этом стоит учитывать и тот факт, что копирование ответов навряд ли пригодится во время контрольной работы, когда нужно будет вспомнить то или иное действие. Так что, чем тщательнее учащиеся разберут теорию и закрепят ее при помощи практики, тем лучше у них будут показатели.
Однако в современных реалиях долго сидеть над учебником просто физически не получится, ведь нужно и по другим дисциплинам уроки делать, и на какие-то кружки еще успеть. Излишняя же торопливость до добра еще никого не доводила. Поэтому использование решебника становится именно тем выходом из трудной ситуации, который одинаково поможет как отличникам, так и двоечникам. Первые с его помощью смогут быстро проверить свой результат и переключиться на следующий предмет, а отстающие ребята без проблем поймут где и в чем они не правы. Работа над ошибками не отнимет много времени, зато правильный алгоритм запомнится намного проще.
В этом году многим подросткам предстоит подготовка к ОГЭ по алгебре. С помощью ГДЗ осуществлять ее будет намного проще, ведь в них представлены все необходимые наглядные примеры. Если что-то подзабылось, можно вернуться к ранее пройденному и повторить тему еще раз. Учителя без сомнения будут довольны, что их подопечные стали намного лучше разбираться в одном из самых сложных предметов школьной программы. При этом не понадобится пользоваться услугами репетиторов, тратить время на дополнительные курсы или изматывать себя просиживанием над тетрадями, в которых все равно ничего не понятно. Просмотреть решебник можно с любого современного устройства, имеющего выход в интернет.
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть — данная прямая. Выберем две точки и так, чтобы прямая была серединным перпендикуляром отрезка (рис. 10.1).
Пусть — произвольная точка прямой Тогда по свойству серединного перпендикуляра отрезка выполняется равенство то есть
![]()
Мы показали, что координаты произвольной точки прямой являются решением уравнения
Теперь покажем, что любое решение уравнения является координатами точки, принадлежащей данной прямой
Пусть — произвольное решение уравнения Тогда ![]() Это равенство означает, что точка равноудалена от точек следовательно, точка принадлежит серединному перпендикуляру отрезка то есть прямой
Это равенство означает, что точка равноудалена от точек следовательно, точка принадлежит серединному перпендикуляру отрезка то есть прямой
Итак, мы доказали, что уравнение является уравнением данной прямой
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: где и — некоторые числа, причем не равны нулю одновременно. Покажем, что уравнение можно преобразовать к такому виду. Возведем обе части уравнения в квадрат. Имеем:
![]()
Раскроем скобки и приведем подобные слагаемые. Получим:
![]()
Обозначив ![]() получим уравнение
получим уравнение
Поскольку точки различны, то хотя бы одна из разностей не равна нулю. Следовательно, числа и не равны нулю одновременно.
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где — некоторые числа, причем не равны нулю одновременно.
Верно и такое утверждение: любое уравнение вида где — некоторые числа, причем не равны нулю одновременно, является уравнением прямой.
Если то графиком уравнения является вся плоскость Если то уравнение не имеет решений.
Из курса алгебры 7 класса вы знаете, что уравнение вида называют линейным уравнением с двумя переменными. Уравнение прямой является частным видом линейного уравнения. Схема, изображенная на рисунке 10.2, иллюстрирует сказанное.
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции является прямая. Сейчас мы можем это доказать.
Перепишем уравнение Мы получили уравнение вида для случая, когда Поскольку в этом уравнении то мы получили уравнение прямой.
А любую ли прямую на плоскости можно задать уравнением вида Ответ на этот вопрос отрицательный.
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой принять то его можно переписать так: Мы получили частный вид уравнения прямой, все точки которой имеют одинаковые абсциссы. Следовательно, эта прямая перпендикулярна оси абсцисс. Ее называют вертикальной.
Если то уравнение прямой можно записать так:
Обозначив получим уравнение
Следовательно, если то уравнение прямой задает вертикальную прямую; если то это уравнение задает невертикальную прямую.
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.

Пример №7
Составьте уравнение прямой, проходящей через точки:
![]()
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая является вертикальной. Ее уравнение имеет вид
2) Поскольку данные точки имеют разные абсциссы, то прямая не является вертикальной. Тогда можно воспользоваться уравнением прямой в виде
Подставив координаты точек в уравнение получаем систему уравнений:
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой и осями координат.
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при получаем
С осью ординат: при получаем
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник (рис. 10.3) с вершинами Найдем стороны треугольника:
Тогда искомые периметр и площадь соответственно равны ![]()
Ответ:
Глава 5. Неравенства:
§31. Свойства числовых неравенств:
31.1
31.2
31.3
31.4
31.5
31.6
31.7
31.8
31.9
31.10
31.11
31.12
31.13
31.14
31.15
31.16
31.17
31.18
31.19
31.20
31.21
31.22
31.23
31.24
31.25
31.26
31.27
31.28
31.29
31.30
31.31
31.32
31.33
31.34
31.35
31.36
31.37
31.38
31.39
31.40
31.41
31.42
31.43
31.44
31.45
31.46
31.47
31.48
31.49
31.50
31.51
31.52
31.53
31.54
31.55
31.56
31.57
31.58
31.59
31.60
31.61
31.62
31.63
31.64
31.65
§32. Исследование функции на монотонность:
32.1
32.2
32.3
32.4
32.5
32.6
32.7
32.8
32.9
32.10
32.11
32.12
32.13
32.14
§33. Решение линейных неравенств:
33.1
33.2
33.3
33.4
33.5
33.6
33.7
33.8
33.9
33.10
33.11
33.12
33.13
33.14
33.15
33.16
33.17
33.18
33.19
33.20
33.21
33.22
33.23
33.24
33.25
33.26
33.27
33.28
33.29
33.30
33.31
33.32
33.33
33.34
33.35
33.36
33.37
33.38
§34. Решение квадратных неравенств:
34.1
34.2
34.3
34.4
34.5
34.6
34.7
34.8
34.9
34.10
34.11
34.12
34.13
34.14
34.15
34.16
34.17
34.18
34.19
34.20
34.21
34.22
34.23
34.24
34.25
34.26
34.27
34.28
34.29
34.30
34.31
34.32
34.33
34.34
34.35
34.36
34.37
34.38
34.39
34.40
34.41
34.42
34.43
34.44
34.45
34.46
§35. Приближённые значения действительных чисел:
35.1
35.2
35.3
35.4
35.5
35.6
35.7
35.8
35.9
35.10
35.11
35.12
§36. Стандартный вид числа:
36.1
36.2
36.3
36.4
36.5
36.6
36.7
36.8
36.9
36.10
36.11
36.12
36.13
36.14
36.15
36.16
36.17
36.18
36.19
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
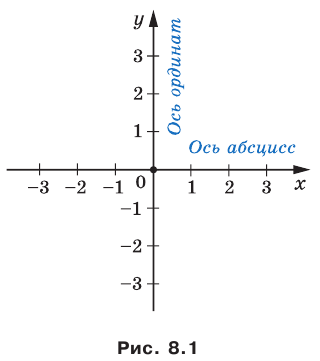
Договорились координатную плоскость с осью
Координаты точки на плоскости называют декартовыми координатами в честь французского математика Рене Декарта (см. рассказ на с. 103).
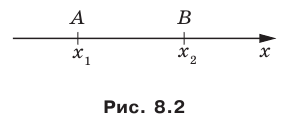
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек (рис. 8.2) имеем:
Научимся находить расстояние между точками заданными на плоскости
Рассмотрим случай, когда отрезок не перпендикулярен ни одной из координатных осей (рис. 8.3).
Через точки проведем прямые, перпендикулярные координатным осям. Получим прямоугольный треугольник в котором Отсюда
Тогда формулу расстояния между точками можно записать так:

Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок перпендикулярен одной из осей координат.
Пусть — точки плоскости Найдем координаты точки — середины отрезка
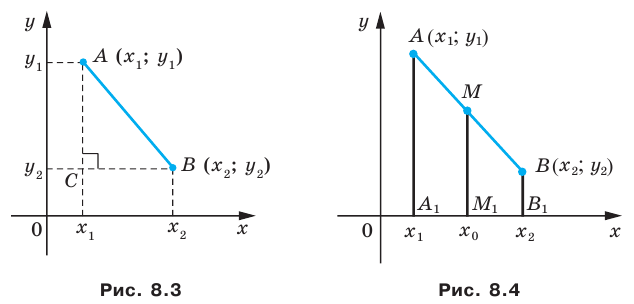
Рассмотрим случай, когда отрезок не перпендикулярен ни одной из координатных осей (рис. 8.4). Будем считать, что (случай, когда рассматривается аналогично). Через точки проведем прямые, перпендикулярные оси абсцисс, которые пересекут эту ось соответственно в точках По теореме Фалеса тогда Поскольку то можем записать: Отсюда Аналогично можно показать что
Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок перпендикулярен одной из осей координат. Докажите это самостоятельно.
Пример №1
Докажите, что треугольник с вершинами в точках является равнобедренным прямоугольным.
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
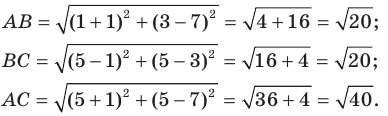
Следовательно, то есть треугольник равнобедренный.
Поскольку то треугольник прямоугольный.
Пример №2
Точка — середина отрезка Найдите координаты точки
Решение:
Обозначим — координаты точки — координаты точки — координаты точки
Поскольку то получаем:
Аналогично ![]()
Ответ:
Пример №3
Докажите, что четырехугольник с вершинами в точках ![]() является прямоугольником.
является прямоугольником.
Решение:
Пусть точка — середина диагонали Тогда
![]()
Следовательно,
Пусть точка — середина диагонали Тогда
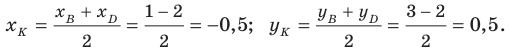
Следовательно,
Таким образом, точки совпадают, то есть диагонали четырехугольника имеют общую середину. Отсюда следует, что четырехугольник — параллелограмм.
Найдем диагонали параллелограмма:
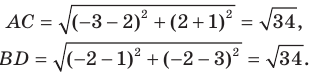
Следовательно, диагонали параллелограмма равны. Отсюда следует, что этот параллелограмм является прямоугольником.
Задания
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
955
956
957
958
959
960
961
962
963
964
965
966
967
968
969
970
971
972
973
974
975
976
977
978
979
980
981
982
983
984
985
986
987
988
989
990
991
992
993
994
995
996
997
Алгебра — долгий путь к успеху
Многие считают алгебру сложным и непонятным предметом. Но это не так
Всегда нужно помнить о том, что в первую очередь важно полное понимание того, что ученик учит. В противном случае можно ругаться, заставлять ребенка сидеть над книгами и т
д., но толку от этого все равно не будет. Чтобы возникло понимание, необходимо дать школьникам полноценную информацию и максимально доступно ее разъяснить. Но не всегда учителям на уроке хватает времени, чтобы предоставить школьникам углубленные знания. А ведь в этом году упускать информацию крайне нецелесообразно, ведь тематика предстоит очень непростая:
- Функции и графики.
- Рациональные уравнения.
- Квадратные корни.
- Системы рациональных уравнений.
- Линейная, дробно-линейная и квадратичная функция.
- Графический способ решения систем уравнения.
Помочь компенсировать это упущение можно с помощью решебника к учебнику «Алгебра 8 класс Никольский, Потапов, Решетников, Шевкин (Просвещение)».
Глава 4. Квадратные уравнения:
§24. Основные понятия:
24.1
24.2
24.3
24.4
24.5
24.6
24.7
24.8
24.9
24.10
24.11
24.12
24.13
24.14
24.15
24.16
24.17
24.18
24.19
24.20
24.21
24.22
24.23
24.24
24.25
24.26
24.27
24.28
24.29
24.30
24.31
24.32
24.33
24.34
24.35
24.36
24.37
24.38
24.39
§25. формулы корней квадратных уравнений:
25.1
25.2
25.3
25.4
25.5
25.6
25.7
25.8
25.9
25.10
25.11
25.12
25.13
25.14
25.15
25.16
25.17
25.18
25.19
25.20
25.21
25.22
25.23
25.24
25.25
25.26
25.27
25.28
25.29
25.30
25.31
25.32
25.33
25.34
25.35
25.36
25.37
25.38
25.39
25.40
25.41
25.42
25.43
25.44
25.45
25.46
25.47
25.48
§26. Рациональные уравнения:
26.1
26.2
26.3
26.4
26.5
26.6
26.7
26.8
26.9
26.10
26.11
26.12
26.13
26.14
26.15
26.16
26.17
26.18
26.19
26.20
26.21
26.22
26.23
26.24
26.25
26.26
26.27
26.28
§27. Рациональнне уравнения как математические модели реальных ситуаций:
27.1
27.2
27.3
27.4
27.5
27.6
27.7
27.8
27.9
27.10
27.11
27.12
27.13
27.14
27.15
27.16
27.17
27.18
27.19
27.20
27.21
27.22
27.23
27.24
27.25
27.26
27.27
27.28
27.29
27.30
27.31
27.32
27.33
27.34
27.35
27.36
27.37
27.38
27.39
27.40
27.41
27.42
27.43
27.44
27.45
§28. Ещё одна формула корней квадратного уравнения:
28.1
28.2
28.3
28.4
28.5
28.6
28.7
28.8
28.9
28.10
28.11
28.12
28.13
28.14
28.15
28.16
28.17
28.18
28.19
28.20
28.21
28.22
28.23
28.24
28.25
28.26
28.27
28.28
§29. Теорема Виета:
29.1
29.2
29.3
29.4
29.5
29.6
29.7
29.8
29.9
29.10
29.11
29.12
29.13
29.14
29.15
29.16
29.17
29.18
29.19
29.20
29.21
29.22
29.23
29.24
29.25
29.26
29.27
29.28
29.29
29.30
29.31
29.32
29.33
29.34
29.35
29.36
29.37
29.38
29.39
29.40
29.41
29.42
29.43
29.44
29.45
29.46
29.47
29.48
29.49
29.50
29.51
29.52
29.53
29.54
29.55
§30. Иррациональные уравнения:
30.1
30.2
30.3
30.4
30.5
30.6
30.7
30.8
30.9
30.10
30.11
30.12
30.13
30.14
30.15
30.16
30.17
30.18
30.19
30.20
30.21
30.22
30.23
30.24
Глава 3. Квадратичная функция у = k/x:
§17. Функция у = кх^2, её свойства и график:
17.1
17.2
17.3
17.4
17.5
17.6
17.7
17.8
17.9
17.10
17.11
17.12
17.13
17.14
17.15
17.16
17.17
17.18
17.19
17.20
17.21
17.22
17.23
17.24
17.25
17.26
17.27
17.28
17.29
17.30
17.31
17.32
17.33
17.34
17.35
17.36
17.37
17.38
17.39
17.40
17.41
17.42
17.43
17.44
17.45
17.46
17.47
17.48
17.49
17.50
17.51
17.52
17.53
17.54
17.55
17.56
17.57
17.58
17.59
17.60
17.61
17.62
17.63
17.64
17.65
17.66
§18. Функция у = k/x её свойства и график:
18.1
18.2
18.3
18.4
18.5
18.6
18.7
18.8
18.9
18.10
18.11
18.12
18.13
18.14
18.15
18.16
18.17
18.18
18.19
18.20
18.21
18.22
18.23
18.24
18.25
18.26
18.27
18.28
18.29
18.30
18.31
18.32
18.33
18.34
18.35
18.36
18.37
18.38
§19. Как построить график функции у = f(x + l), если известен график функции у = f(x):
19.1
19.2
19.3
19.4
19.5
19.6
19.7
19.8
19.9
19.10
19.11
19.12
19.13
19.14
19.15
19.16
19.17
19.18
19.19
19.20
19.21
19.22
19.23
19.24
19.25
19.26
19.27
19.28
19.29
19.30
19.31
19.32
19.33
19.34
19.35
19.36
19.37
19.38
19.39
19.40
19.41
19.42
19.43
19.44
19.45
19.46
19.47
19.48
19.49
19.50
19.51
19.52
19.53
19.54
19.55
19.56
19.57
19.58
§20. Как построить график функции у = f(x) + т, если известен график функции у = f(т):
20.1
20.2
20.3
20.4
20.5
20.6
20.7
20.8
20.9
20.10
20.11
20.12
20.13
20.14
20.15
20.16
20.17
20.18
20.19
20.20
20.21
20.22
20.23
20.24
20.25
20.26
20.27
20.28
20.29
20.30
20.31
20.32
20.33
20.34
20.35
20.36
20.37
20.38
20.39
20.40
20.41
20.42
§21. Как построить график функции у = f(x+l)+m, если известен график функции y=f(x):
21.1
21.2
21.3
21.4
21.5
21.6
21.7
21.8
21.9
21.10
21.11
21.12
21.13
21.14
21.15
21.16
21.17
21.18
21.19
21.20
21.21
21.22
21.23
21.24
21.25
21.26
21.27
21.28
21.29
§22. Функция у = ах^2+Ьх+с, её свойства и график:
22.1
22.2
22.3
22.4
22.5
22.6
22.7
22.8
22.9
22.10
22.11
22.12
22.13
22.14
22.15
22.16
22.17
22.18
22.19
22.20
22.21
22.22
22.23
22.24
22.25
22.26
22.27
22.28
22.29
22.30
22.31
22.32
22.33
22.34
22.35
22.36
22.37
22.38
22.39
22.40
22.41
22.42
22.43
22.44
22.45
22.46
22.47
22.48
22.49
22.50
22.51
22.52
22.53
22.54
22.55
§23. Графическое решение квадратных уравнений:
23.1
23.2
23.3
23.4
23.5
23.6
23.7
23.8
23.9
23.10
23.11
23.12
23.13
23.14
23.15
23.16
23.17
23.18
23.19
23.20
23.21
23.22
23.23
23.24
Глава 2. Функция у = у/х. Свойства квадратного корня:
§9. Рациональные числа:
9.1
9.2
9.3
9.4
9.5
9.6
9.7
9.8
9.9
9.10
9.11
9.12
9.13
9.14
9.15
9.16
9.17
9.18
9.19
9.20
9.21
9.22
9.23
9.24
9.25
9.26
9.27
9.28
9.29
§10. Понятие квадратного корня из неотрицательного числа:
10.1
10.2
10.3
10.4
10.5
10.6
10.7
10.8
10.9
10.10
10.11
10.12
10.13
10.14
10.15
10.16
10.17
10.18
10.19
10.20
10.21
10.22
10.23
10.24
10.25
10.26
10.27
10.28
10.29
10.30
10.31
10.32
10.33
10.34
10.35
10.36
10.37
10.38
10.39
10.40
10.41
10.42
10.43
§11. Иррациональные числа:
11.1
11.2
11.3
11.4
11.5
11.6
11.7
11.8
11.9
11.10
11.11
11.12
11.13
11.14
11.15
11.16
11.17
§12. Множество действительных чисел:
12.1
12.2
12.3
12.4
12.5
12.6
12.7
12.8
12.9
12.10
12.11
12.12
12.13
12.14
12.15
12.16
12.17
12.18
12.19
12.20
12.21
12.22
§13. Функция у = х^0.5, её свойства и график:
13.1
13.2
13.3
13.4
13.5
13.6
13.7
13.8
13.9
13.10
13.11
13.12
13.13
13.14
13.15
13.16
13.17
13.18
13.19
13.20
13.21
13.22
13.23
13.24
13.25
13.26
13.27
13.28
13.29
13.30
13.31
13.32
§14. Свойства квадратных корней:
14.1
14.2
14.3
14.4
14.5
14.6
14.7
14.8
14.9
14.10
14.11
14.12
14.13
14.14
14.15
14.16
14.17
14.18
14.19
14.20
14.21
14.22
14.23
14.24
14.25
14.26
14.27
14.28
14.29
14.30
14.31
14.32
14.33
14.34
14.35
14.36
§15. Преобразование выражений, содержащих операцию извлечения квадратного корня:
15.1
15.2
15.3
15.4
15.5
15.6
15.7
15.8
15.9
15.10
15.11
15.12
15.13
15.14
15.15
15.16
15.17
15.18
15.19
15.20
15.21
15.22
15.23
15.24
15.25
15.26
15.27
15.28
15.29
15.30
15.31
15.32
15.33
15.34
15.35
15.36
15.37
15.38
15.39
15.40
15.41
15.42
15.43
15.44
15.45
15.46
15.47
15.48
15.49
15.50
15.51
15.52
15.53
15.54
15.55
15.56
15.57
15.58
15.59
15.60
15.61
15.62
15.63
15.64
15.65
15.66
15.67
15.68
15.69
15.70
15.71
15.72
15.73
15.74
15.75
15.76
15.77
15.78
15.79
15.80
15.81
15.82
15.83
15.84
15.85
15.86
15.87
15.88
15.89
15.90
15.91
15.92
15.93
15.94
15.95
15.96
15.97
15.98
15.99
15.100
15.101
15.102
15.103
15.104
15.105
15.106
§16. Модуль действительного числа:
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
16.10
16.11
16.12
16.13
16.14
16.15
16.16
16.17
16.18
16.19
16.20
16.21
16.22
16.23
16.24
16.25
16.26
16.27
16.28
16.29
16.30
16.31
16.32
16.33
16.34
16.35
16.36
16.37
16.38
16.39
16.40
16.41
16.42
16.43
16.44
Стоит ли акцентировать внимание на решебник
Уроки по алгебре в большинстве школ идут три дня в неделю, т.е. откладывать выполнение упражнений на потом не очень-то и получается. Из-за этого школьники начинают торопиться и часто допускают недочеты. Это в свою очередь приводит к снижению оценок. К тому же, многие ребята совершенно игнорируют теорию, представленную в учебнике, что в корне неверно. Существует и другая проблема — отсутствие объяснений в учебном пособии как таковых. Если еще и учитель не даст пояснений по теме, то можно считать, что пробел в знаниях обеспечен.
Как избежать недопониманий в учебе? Каким образом предотвратить падение успеваемости? Чем помочь учащимся? Кто-то спешит нанять репетиторов, некоторые ищут всевозможные курсы. Но приносят ли эти методы реальную пользу? Если повезет найти хорошего профессионала, то возможно результат и будет положительным. В противном же случае ожидать чего-то путного не стоит. Хорошим способом уяснить текущую программу многие считают ГДЗ по алгебре 8 класс Учебник Никольский (Просвещение). Почему? Давайте разберемся:
- В решебнике вся информация изложена предельно доступным образом.
- Все представленные ответы и решения написаны учителями с большим стажем, так что в них можно не сомневаться.
- Сборник соответствует всем требованиям ФГОС.
- Пособие постоянно обновляется, так что сведения на сайте всегда актуальны.
- По особо проблемным случаям есть дополнительные комментарии, которые позволят лучше разобраться в конкретном случае.
Таким образом, данный справочник с полным основанием можно назвать полноценным методическим пособием, которое поможет преодолеть любые недопонимания по предмету.
Глава 1. Алгебраические дроби:
§1. Основные понятия:
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.19
1.20
1.21
1.22
1.23
1.24
1.25
1.26
1.27
1.28
1.29
1.30
1.31
1.32
1.33
1.34
1.35
1.36
1.37
1.38
1.39
1.40
1.41
§2. Основное свойство алгебраической дроби:
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2.16
2.17
2.18
2.19
2.20
2.21
2.22
2.23
2.24
2.25
2.26
2.27
2.28
2.29
2.30
2.31
2.32
2.33
2.34
2.35
2.36
2.37
2.38
2.39
2.40
2.41
2.42
2.43
2.44
2.45
2.46
§3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями:
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11
3.12
3.13
3.14
3.15
3.16
3.17
3.18
3.19
3.20
3.21
3.22
3.23
3.24
3.25
3.26
3.27
3.28
3.29
§4. Сложение и вычитание алгебраических дробей с разными знаменателями:
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.18
4.19
4.20
4.21
4.22
4.23
4.24
4.25
4.26
4.27
4.28
4.29
4.30
4.31
4.32
4.33
4.34
4.35
4.36
4.37
4.38
4.39
4.40
4.41
4.42
4.43
4.44
4.45
4.46
4.47
4.48
4.49
4.50
4.51
4.52
4.53
4.54
4.55
4.56
§5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степен:
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
5.13
5.14
5.15
5.16
5.17
5.18
5.19
5.20
5.21
5.22
5.23
5.24
5.25
5.26
5.27
5.28
5.29
5.30
5.31
5.32
5.33
5.34
5.35
5.36
5.37
5.38
5.39
5.40
5.41
5.42
5.43
5.44
5.45
5.46
§6. Преобразование рациональных выражений:
6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.12
6.13
6.14
6.15
6.16
6.17
6.18
6.19
6.20
6.21
6.22
6.23
6.24
§7. Первые представления о рациональных уравнениях:
7.1
7.2
7.3
7.4
7.5
7.6
7.7
7.8
7.9
7.10
7.11
7.12
7.13
7.14
7.15
7.16
7.17
7.18
7.19
7.20
7.21
7.22
7.23
7.24
7.25
7.26
7.27
7.28
7.29
7.30
7.31
7.32
7.33
7.34
7.35
7.36
7.37
7.38
7.39
7.40
§8. Степень с отрицательным целым показателем:
8.1
8.2
8.3
8.4
8.5
8.6
8.7
8.8
8.9
8.10
8.11
8.12
8.13
8.14
8.15
8.16
8.17
8.18
8.19
8.20
8.21
8.22
8.23
8.24
8.25
8.26
8.27
8.28
8.29
8.30
8.31
8.32



















