Гдз по математике 5 класс виленкин

Свойства деления целых чисел

Рассуждая о смысле деления целых чисел , мы выяснили, что деление целых чисел – это действие, обратное умножению. Мы дали такое определение: деление целых чисел – это нахождение неизвестного множителя по известному произведению и известному множителю. То есть, целое число c
мы называем частным от деления целого числа a
на целое число b
, когда произведение c·b
равно a
.

Данное определение, а также все рассмотренные выше свойства операций над целыми числами позволяют установить справедливость следующих свойств деления целых чисел:

• Никакое целое число нельзя делить на нуль.
• Свойство деления нуля на произвольное целое число a
  , отличное от нуля: 0:a=0
  .
• Свойство деления равных целых чисел: a:a=1
  , где a
  – любое целое число, отличное от нуля.
• Свойство деления произвольного целого числа a
  на единицу: a:1=a
  .
• В общем случае деление целых чисел НЕ обладает переместительным свойством: a:b≠b:a
  .
• Свойства деления суммы и разности двух целых чисел на целое число: (a+b):c=a:c+b:c
  и (a−b):c=a:c−b:c
  , где a
  , b
  , и c
  такие целые числа, что и a
  и b
  делится на c
  , и c
  отлично от нуля.
• Свойство деления произведения двух целых чисел a
  и b
  на целое число c
  , отличное от нуля: (a·b):c=(a:c)·b
  , если a
  делится на c
  ; (a·b):c=a·(b:c)
  , если b
  делится на c
  ; (a·b):c=(a:c)·b=a·(b:c)
  , если и a
  и b
  делятся на c
  .
• Свойство деления целого числа a
  на произведение двух целых чисел b
  и c
  (числа a
  , b
  и c
  такие, что деление a
  на b·c
  возможно): a:(b·c)=(a:b)·c=(a:c)·b
  .
• Любые другие свойства деления целых чисел.

Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц.Числа 3 и 4, которые мы сложили называется слагаемыми
. А результат сложение число 7 называется суммой
.

Сумма
— это сложение чисел. Знак плюс “+”.В буквенном виде этот пример будет выглядеть так:

a+
b=
c

Компоненты сложения:a
— слагаемое, b
— слагаемые, c
– сумма.
Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.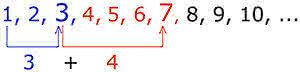
Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:

Называется такое свойство слагаемых переместительным законом сложения
.

ГДЗ к учебнику по математике для 5 класс Перовой М. Н., Капустиной Г. М. (Просвещение) и его польза для пятиклассников

Электронный ресурс станет надежным консультантом пятиклассникам в получении среднего образования. Учебно-методический справочник составлен по аналогии с основным учебником и содержит в себе несколько тестовых заданий, математических диктантов и даже индивидуальные задания, которые представлены в двух вариантах исполнения. Авторы издания – Капустина и Перова, представили точные развёрнутые ответы с пояснениями и комментариями, стандарты которых соответствуют всем нормам ФГОС. Для нахождения верного ответа, требуется лишь зайти на портал с телефона, ноутбука или планшета и выбрать необходимый номер.

Наша книжечка всегда придёт на помощь в трудную минуту и благоприятно повлияет на повышение академической успеваемости ребёнка. Главные преимущества решебника заключаются в следующем. Во-первых, в полной форме приведены ответы на задания, с развёрнутыми комментариями и пояснениями авторов, форма которых полностью соответствует всем требованиям ФГОС. Во-вторых, благодаря ГДЗ ребёнок самостоятельно выполнит домашнюю работу, не прибегая к помощи родителей. В-третьих, издание доступно онлайн, воспользоваться им можно с любого современного устройства, поддерживающего подключение к интернету. Помимо школьников, пособие принесёт неизмеримую поддержку учителям, которые могут использовать материалы для составления собственного методического плана, и значительно сократят время на проверку бесчисленного количества тетрадей. Желаем удачи!

Переместительный закон сложения.

От перемены мест слагаемых сумма не меняется.

В буквенной записи переместительный закон выглядит так:

a+
b=
b+
a

Если мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 4. И выполним сложение в таком порядке, сначала прибавим 1+2, а потом выполним сложение к получившейся сумме 4, то получим выражение:

(1+2)+4=7

Можем сделать наоборот, сначала сложить 2+4, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так:

1+(2+4)=7

Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод:

(1+2)+4=1+(2+4)

Это свойство сложения называется сочетательным законом сложения
.

Переместительный и сочетательный закон сложения работает для всех неотрицательных чисел.

Ответы к стр. 35

Какое число надо прибавить к натуральному числу, чтобы получилось следующее за ним число?Какие числа называют слагаемыми?Что называют суммой двух чисел?Сформулируйте переместительное свойство сложения.Сформулируйте сочетательное свойство сложения.Изменяется ли число, если к нему прибавить нуль?Чему равна сумма нуля и числа?Что такое периметр треугольника?

Если прибавить к натуральному числу единицу, то получится следующее за ним число: 2 + 1 = 3, 3 + 1 = 4.
Числа, которые складывают: 3 + 5 = 8.
Число, получающееся при сложение чисел: 3 + 5 = 8.
Сумма чисел не изменяется при перестановке слагаемых.
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом к полученной сумме — второе слагаемое.
От прибавления нуля число не изменяется.
Если прибавить к нулю какое-нибудь число, то получится прибавленное число.
Сумма длин его сторон.

182. Найдите суммы: 999 + 1; 78 099 + 1; 999 999 + 1.

999 + 1 = 1000;
78 099 + 1 = 78 100;
999 999 + 1 = 1 000 000.

183. Найдите сумму 76 + 24. Сколько единиц надо прибавить к числу 76, чтобы получить 100?

76 + 24 = 100, к числу 76 надо прибавить 24 единицы, или 24 раза по единице, чтобы получить 100.

184. Купили 3 кг картофеля, 3 кг свёклы, 4 кг моркови, 5 кг яблок, 6 кг капусты, 2 кг груш и 4 кг слив. Сколько было куплено килограммов овощей и сколько килограммов фруктов?

Овощи — картофель, свёкла, морковь, капуста.
Фрукты — яблоки, груши, сливы.
1) 3 + 3 + 4 + 6 = 16 (кг) — овощи
2) 5 + 2 + 4 = 11 (кг) — фрукты
О т в е т: купили 16 кг овощей и 11 кг фруктов.

185. Две девочки собирали в лесу малину. Первая девочка собрала 1 кг 250 г малины, а вторая — на 300 г больше. Сколько граммов малины собрали две девочки вместе?

1 кг 250 г = 1250 г
1) 1250 + 300 = 1550 (г) — собрала вторая девочка
2) 1250 + 1550 = 2800 (г) — собрали вместе
О т в е т: девочки собрали 2800 г малины.

186. В одной пачке 23 книги и в ней на 8 книг меньше, чем во второй, а в третьей пачке на 6 книг больше, чем во второй. Сколько всего книг в трёх пачках?

1) 23 + 8 = 31 (к.) — во второй пачке
2) 31 + 6 = 37 (к.) — в третьей пачке
3) 23 + 31 + 37 = 91 (к.) — всего
О т в е т: в трёх пачках 91 книга.

187. В первый день собрали 127 т картофеля, что на 32 т меньше, чем во второй день. В третий день собрано на 40 т больше, чем в первый день. Сколько всего тонн картофеля было собрано за эти три дня?

1) 127 + 32 = 159 (т) — собрали во второй день
2) 127 + 40 = 167 (т) — собрали в третий деньв) 127 + 159 + 167 = 453 (т) — собрали всего
О т в е т: за три дня собрали 453 т картофеля.

188. Начертите координатный луч и отметьте на нём точку С(6), отложите от этой точки вправо 5 единичных отрезков и отметьте точку D. Чему равна координата точки D?

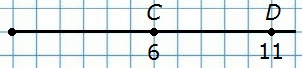
6 + 5 = 11 — координата точки D.

189. Начертите координатный луч и отметьте на нём точки М(7) и Т(15). Сколько единичных отрезков надо отложить от точки М и в какую сторону, чтобы попасть в точку T?

15 — 7 = 8 — 8 единичных отрезков вправо.

190. Изобразите на координатном луче сложение:
4 + 3; 4 + 6; 4 + 8; 8 + 4.

191. Выполните действия: а) (457 + 705) + 295; б) 554 + (46 + 1425).

а) (457 + 705) + 295 = 457 + (705 + 295) = 457 + 1000 = 1457;
б) 554 + (46 + 1425) = (554 + 46) + 1425 = 600 + 1425 = 2025.

192. Вычислите сумму, выбирая удобный порядок выполнения действий: а) 385 + 548 + 615; б) 221 + 427 + 373.

а) 385 + 548 + 615 = (385 + 615) + 548 = 1000 + 548 = 1548;
б) 221 + 427 + 373 = 221 + (427 + 373) = 221 + 800 = 1021.

193. Вычислите:
а) 458 + 333 + 42 + 67;
б) 635 + 308 + 1365 + 392;
в) 411 + 419 + 145 + 725 + 87;
г) 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19.

а) 458 + 333 + 42 + 67 = (458 + 42) + (333 + 67) = 500 + 400 = 900;
б) 635 + 308 + 1365 + 392 = (635 + 1365) + (308 + 392) = 2000 + 700 = 2700;
в) 411 + 419 + 145 + 725 + 87 = (411 + 419) + (145 + 725) + 87 = 830 + 870 + 87 = 1700 + 87 = 1787;
г) 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 = (11 + 19) + (12 + 18) + (13 + 17) + (14 + 16) + 15 = 30 + 30 + 30 + 30 + 15 = 135.

← Предыдущая

Следующая →

Персональный онлайн-репетитор к учебнику по математике за 5 класс Перовой

Материалы решебника желательно всегда держать под рукой, чтобы воспользоваться готовыми ответами даже во время урока. Но это не проблема, так как книга находится в электронном доступе. Зайти на страницы ГДЗ можно с ноутбука, смартфона или любого другого устройства с выходом в Интернет. Это практично и очень удобно. Ученику не придется часами листать учебное пособие, чтобы найти нужную информацию. Для этого достаточно ввести в строку поиска номер задания. Через пару секунд на экране гаджета появятся результаты.

Сегодня с уверенностью можно сказать, что ГДЗ по математике для пятиклассников является ярким примером современного и качественного учебного пособия. С его помощью ребенок сможет адаптироваться к новым условиям и требованиям средней школы, преодолеть возможные трудности, а также добиться впечатляющих предметных результатов:

• работать с математическим текстом (анализировать, извлекать необходимую информацию), грамотно применять математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический);
• выполнять устные, письменные, инструментальные вычисления; проводить несложные практические расчёты с использованием при необходимости справочных материалов, калькулятора, компьютера;
• точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику; обосновывать суждения, проводить классификацию, обосновывать математические утверждения;
• записывать и читать натуральные числа;
• изображать отрезок, заданной длины, и находить длину заданного отрезка;
• изображать прямую, луч, треугольник;
• вычислять периметр треугольника;
• изображать натуральные числа на координатном луче.

Помимо прочего, на уроках школьников ждут увлекательные математические опыты и эксперименты. Они научатся объяснять их результаты и получат навыки в правильном их описании. Значительная часть нашей жизни проходит в режиме онлайн. Сфера образования не осталась в стороне, поэтому в сети сегодня можно найти любую актуальную учебную литературу. Прибегая к использованию онлайн-решебников, ребенок учится пользоваться Интернетом как учебным ресурсом и постепенно привыкает выполнять домашнее задание самостоятельно. Удобный и практичный решебник всегда готов подсказать верный ответ. Пособие доступно с любого гаджета, а значит им так легко воспользоваться дома и в школе. Поэтому теперь вовсе не нужно хранить в шкафу объемную дополнительную литературу и тем более носить ее в портфеле.

Чем еще полезен ГДЗ к учебнику по математике за 5 класс Перовой

Решебник имеется в свободном доступе в интернете. Его навигация настолько проста, что позволяет найти верный ответ за считанные секунды. Во-первых, школьник сможет моментально получить обратную связь, достаточно для этого внести в поисковую строку номер задания. Во-вторых, с ним можно не быть привязанным к одному месту. И, в-третьих, структура решебника хорошо продуманна и сбалансирована. Итак, наш портал способен помочь каждому. Не имеет значения, каким уровнем знаний в области математики обладает ученик. Он способен каждого научить многим моментам и отточить навыки пользования вычислительными машинами в совершенстве.

Огромное значение имеет математика при формировании взгляда ребёнка на окружающий его мир. Без знаний этого предмета невозможно иметь представление о формулах, теоремах, аксиомах, доказательствах, правилах и др. Успешно освоить данную дисциплину не представится возможным, если не применять полученные знания на практике в комплексе с рабочими тетрадями и решением тестовых заданий. А поможет в этом только наше онлайн-пособие, без которого не обойтись ни одному современному школяру.

1. Обозначение натуральных чисел. Плоскость. Прямая. Луч. Шкалы и координаты. Меньше или больше. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания.
2. Умножение натуральных чисел и его свойства. Деление натуральных чисел и его свойства. Деление с остатком. Упрощение выражений. Порядок выполнения действий.
3. Степень числа. Квадрат и куб числа. Площадь. Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объём прямоугольного параллелепипеда.

Публикация «Рабочий лист для 5 класса для отработки навыков буквенной записи свойств сложения и вычитания, решения уравнений» размещена в разделах

• Математика. Сложение и вычитание. Конспекты уроков
• Средняя школа, 5 класс
• Средняя школа. 5-9 классы
• Школа. Материалы для школьных педагогов
• Темочки

3. Свойство нуля при сложении: a + 0 = 0 + a = а.

4. Свойство вычитания суммы из числа: a – (b + с) = a – b – с, где b + с < a или b + с = a.

5. Свойство вычитания числа из суммы:

(a + b) – с = a + (b – с, если с < b или с = b;

(a + b) – с = (a – с) + b, если с < а или с = а.

6. Свойство нуля при вычитании: а – 0 = а; а – а = 0.

Пример: Найдите значение выражения 3284 – (а + 72) при а = 2714.

Решение: Если а = 2714, то 3284 – (а + 72) = 3284 – (2714 + 72) = (3284 – 2714) – 72 = 570 – 72 = 498.

Ответ: 498.

Определение 1: Уравнением называется равенство, содержащее букву, значение которой надо найти.

Определение 2: Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. Решить уравнение – значит найти все его корни (или убедиться, что корней нет).

Правило 1: Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

Пример: х + 25 = 768 (х + 15) + 14 = 56 (х – 13) + 23 = 78

х = 768 – 25 х + 15 = 56 — 14 х – 13 = 78 — 23

х = 743 х + 15 = 42 х – 13 = 55

х = 42 – 15 х = 55 + 13

х = 27 х = 68

Правило 2: Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность.

Пример: у – 284 = 72

у = 72 + 284

у = 356

Правило 3: Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

Пример: 3286 – z = 290

z = 3286 – 290

z = 2996

8. Умение: Решать текстовые задачи арифметическим способом.

Правило: Любая задача состоит из условия и требования.

В условии указаны сведения о некоторых объектах и величины, характеризующие эти объекты.

В требовании указано то, что нужно найти.

Для решения задачи нужно установить связь между искомыми и исходными данными и записать её в виде числового выражения.

Примеры: 1) Кит длиннее, чем акула, на 20 м. Какова длина акулы, если длина кита 33 м?

Решение: 33 – 20 = 13 (м).

Ответ: 13 м.

2) В троллейбусе ехало 47 пассажиров. На остановке 12 пассажиров вышли и 15 вошли. Сколько стало пассажиров в троллейбусе?

Решение: 47 – 12 + 15 = (47 – 12) + 15 = 35 + 15 = 50.

Ответ: 50 пассажиров.

Правило: Обозначаем искомую величину буквой, составляем равенство на основе описанных в задаче зависимостей. Решаем полученное уравнение и отвечаем на главный вопрос задачи.

Пример: В корзине было 60 грибов. После того как в неё положили ещё несколько грибов, их стало 73. Сколько грибов положили в корзину?

Решение: Пусть х грибов положили в корзину, тогда в корзине стало (60 + х) грибов. Зная, что в корзине стало 73 гриба, составим уравнение.

60 + х = 73

х = 73 – 60

х = 13 Ответ: 13 грибов положили в корзину.

Выполните задания

6. Умения: Записывать и использовать буквенную запись свойств сложения и вычитания для нахождения значения числового и буквенного выражения.

Система задач.

1. Найдите значения выражений.

а) 3721 + а, при а = 2836;

б) 37241 – т + п, при т = 728, п = 44521;

в) (327 + х) – (624 – у, при х = 8236, у = 324.

2. Запишите числовое выражение, соответствующее по смыслу «Сумма разности х и 283 и суммы a и b», и найдите его значение при х = 372, a = 3254, b = 721.

7. Умения: Распознавать уравнение, содержащее в записи знаки «+» и «–», и находить его корень.

Система задач.

1. Решите уравнения.

а) х + 28 = 762 в) т – 25 = 682 д) (х + 15) + 73 = 102

б) 354 + у = 372 г) 3572 – п = 3500 е) (356 + 244) – у = 12

2. Решите уравнение (a + b) – х = c + d, при а = 72, b = 824, c = 11, d = 7.

8. Умение: Решать текстовые задачи арифметическим способом.

Система задач.

1. У мамы было 500 рублей. После оплаты счёта за телефон у неё осталось 134 рубля. Сколько рублей заплатила мама?

2. В ящике было 15 кг картофеля. После того как в ящик досыпали ещё некоторое количество картофеля, его вес составил 56 кг. Сколько картофеля досыпали в ящик?

3. К числу 782 прибавили 732, затем вычли из результата некоторое число х и ещё прибавили 37, получив в результате 1000. Найдите число х.

10. Умения: Моделировать условие текстовой задачи и решать аналитическим способом (с помощью уравнения, содержащего в записи знаки «+» и «–»).

Система задач.

1. Какое уравнение соответствует условию задачи: «Мише 12 лет. Если к возрасту Миши прибавить возраст его папы, то получится 45. Сколько лет Мишиному папе?».

а) 12 – х = 45; б) 45 + 12 = х; в) 12 + х = 45.

2. Решите задачу.

В первый день Оля прочитала 10 страниц из книги. Каждый следующий день Оля читала на одно и то же количество страниц больше, чем в предыдущий день. На сколько страниц в день читала Оля больше, если всего она прочитала за три дня 39 страниц?

Свойство вычитания с нулем.

10 — 0 = 10
a — 0 = a

Если из числа вычесть нуль
то, будет тоже самое число.

10 — 10 = 0
a —
a = 0

Если из числа вычесть тоже самое число
то, будет нуль.

Вопросы по теме:В примере 35 — 22 = 13 назовите уменьшаемое, вычитаемое и разность.

Ответ: 35 – уменьшаемое, 22 – вычитаемое, 13 – разность.

Если числа одинаковые, чему равна их разность?

Ответ: нуль.

Сделайте проверку вычитания 24 — 16 = 8?

Ответ: 16 + 8 = 24

Таблица вычитания натуральных чисел от 1 до 10.

Примеры на задачи по теме «Вычитание натуральных чисел».

Пример №1:


Вставьте пропущенное число: а)20 — … = 20 б) 14 — … + 5 = 14
Ответ: а) 0 б) 5

Пример №2:


Можно ли выполнить вычитание: а) 0 — 3 б) 56 — 12 в) 3 — 0 г) 576 — 576 д) 8732 — 8734
Ответ: а) нет б) 56 — 12 = 44 в) 3 — 0 = 3 г) 576 — 576 = 0 д) нет

Пример №3:


Прочитайте выражение: 20 — 8
Ответ: “От двадцати отнять восемь” или “из двадцати вычесть восемь”. Правильно произносить слова

Мы определили сложение, умножение, вычитание и деление целых чисел. Эти действия (операции) обладают рядом характерных результатов, которые называются свойствами. В этой статье мы рассмотрим основные свойства сложения и умножения целых чисел, из которых следуют все остальные свойства этих действий, а также свойства вычитания и деления целых чисел.

Навигация по странице.

Для сложения целых чисел характерны еще несколько очень важных свойств.

Одно из них связано с существованием нуля. Это свойство сложения целых чисел утверждает, что прибавление к любому целому числу нуля не изменяет это число
. Запишем данное свойство сложения с помощью букв: a+0=a
и 0+a=a
(это равенство справедливо в силу переместительного свойства сложения), a
– любое целое число. Можно услышать, что целое число нуль называют нейтральным элементом по сложению. Приведем пару примеров. Сумма целого числа −78
и нуля равна −78
; если к нулю прибавить целое положительное число 999
, то в результате получим число 999
.

Сейчас мы дадим формулировку еще одного свойства сложения целых чисел, которое связано с существованием противоположного числа для любого целого числа. Сумма любого целого числа с противоположным ему числом равна нулю
. Приведем буквенную форму записи этого свойства: a+(−a)=0
, где a
и −a
– противоположные целые числа. Например, сумма 901+(−901)
равна нулю; аналогично сумма противоположных целых чисел −97
и 97
равна нулю.

Распределительное свойство умножения целых чисел относительно сложения

Совместно сложение и умножение целых чисел нам позволяет рассматривать распределительное свойство умножения относительно сложения, которое связывает два указанных действия. Использование сложения и умножения совместно открывает дополнительные возможности, которых мы были бы лишены, рассматривая сложение отдельно от умножения.

Итак, распределительное свойство умножения относительно сложения гласит, что произведение целого числа a на сумму двух целых чисел a
и b
равно сумме произведений a·b
и a·c
, то есть, a·(b+c)=a·b+a·c

. Это же свойство можно записать в другом виде: (a+b)·c=a·c+b·c

.

Распределительное свойство умножения целых чисел относительно сложения вместе с сочетательным свойством сложения позволяют определить умножение целого числа на сумму трех и большего количества целых чисел, а далее – и умножение суммы целых чисел на сумму.

Также заметим, что все остальные свойства сложения и умножения целых чисел могут быть получены из указанных нами свойств, то есть, они являются следствиями указанных выше свойств.

Что такое сложение?

{"questions":[{"instruction":"Начнем с самого простого: $1 + 3 = ?$","content":"`image-1`У вас есть одно яблоко, ваш лучший друг поделился с вами еще тремя яблоками. Сколько у вас сейчас яблок?`choice-6`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/08/yabloki-01-1.svg"},"choice-6":{"type":"choice","options":,"explanations":,"answer":}},"hints":}]}

А теперь задачка посложнее.

{"questions":[{"instruction":"Сколько будет $5 + 6$?","content":"Итак, у нас есть пять яблок. Мы сорвали с ветки еще шесть яблок `image-1` Теперь у нас `fill_choice_big-10` яблок.","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2021/08/slozhenie-yabloki.svg"},"fill_choice_big-10":{"type":"fill_choice_big","options":,"answer":0}},"step":1,"hints":["Считаем по нашей картинке: раз, два, три, четыре, пять...<br /><br />","Всего у нас стало $11$ яблок."]}]}

Сложить числа $5$ и $6$ — значит прибавить к числу $5$ единицу $6$ раз

{"questions":[{"content":"Образавр купил $5$ томатов, $4$ огурца, $3$ луковицы и $1$ сладкий перец. Сколько всего овощей купил Образавр?`image-1``choice-5`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/08/frukty-ovoshhi.svg"},"choice-5":{"type":"choice","options":,"answer":}},"hints":}]}

Основные свойства умножения целых чисел

Умножению целых чисел присущи все свойства умножения натуральных чисел . Перечислим основные из этих свойств.

Также как нуль является нейтральным целым числом относительно сложения, единица является нейтральным целым числом относительно умножения целых чисел. То есть, умножение любого целого числа на единицу не изменяет умножаемое число
. Так 1·a=a
, где a
– любое целое число. Последнее равенство можно переписать в виде a·1=a
, это нам позволяет сделать переместительное свойство умножения. Приведем два примера. Произведение целого числа 556
на 1
равно 556
; произведение единицы и целого отрицательного числа −78
равно −78
.

Следующее свойство умножения целых чисел связано с умножением на нуль. Результат умножения любого целого числа a
на нуль равен нулю
, то есть, a·0=0
. Также справедливо равенство 0·a=0
в силу переместительного свойства умножения целых чисел. В частном случае при a=0
произведение нуля на нуль равно нулю.

Для умножения целых чисел также справедливо свойство, обратное к предыдущему. Оно утверждает, что произведение двух целых чисел равно нулю, если хотя бы один из множителей равен нулю
. В буквенном виде это свойство можно записать так: a·b=0
, если либо a=0
, либо b=0
, либо и a
и b
равны нулю одновременно.

Свойства вычитания целых чисел

Из полученного равенства, а также из свойств сложения и умножения целых чисел вытекают следующие свойства вычитания целых чисел (a
, b
и c
– произвольные целые числа):

• Вычитание целых чисел в общем случае НЕ обладает переместительным свойством: a−b≠b−a
  .
• Разность равных целых чисел равна нулю: a−a=0
  .
• Свойство вычитания суммы двух целых чисел из данного целого числа: a−(b+c)=(a−b)−c
  .
• Свойство вычитания целого числа из суммы двух целых чисел: (a+b)−c=(a−c)+b=a+(b−c)
  .
• Распределительное свойство умножения относительно вычитания: a·(b−c)=a·b−a·c и (a−b)·c=a·c−b·c
  .
• И все другие свойства вычитания целых чисел.

Сложение с помощью координатного луча

А сейчас давайте познакомимся с другим способом счета — c помощью координатного луча.

Решим пример: $3+4$.

Нарисуем луч, на котором отметим числа по порядку: $0, 1, 2, 3…$

Рисунок $2$ Координатный луч

Нам нужно к $3$ прибавить $4$. Отметим тройку на координатном луче (рисунок $3$):

Рисунок $3$

Чтобы прибавить $4$, нам нужно «прошагать» по лучу вправо четыре шага. И посмотреть, к какому числу мы придем.

Рисунок $4$ Вычисление с помощью координатного луча

Мы пришли к семерке. Это и будет наш ответ. Вот так просто.

$3 + 4 = 7$

Для того, чтобы сложить числа от $0$ до $25$, в качестве координатного луча можно использовать школьную линейку:

Со временем вы будете совершать эти операции в уме не задумываясь. Потренируйтесь на нашем тренажёре сложения в пределах 10.

{"questions":[{"content":"Сложите с помощью координатного луча числа $3$ и $5$:`image-8`<br />`choice-1`","widgets":{"choice-1":{"type":"choice","options":,"answer":},"image-8":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2021/08/positive-coord-3.svg"}},"step":1,"hints":}]}