Ответы к стр. 128
570. а) Что называют многоугольником?
б) Что называют сторонами, углами, вершинами многоугольника?
в) Что называют периметром многоугольника?
г) Какой многоугольник называют выпуклым?
д) Какие многоугольники называют равными?
а) Фигуру, образованную ломаной линией, конец которой совпадает с её началом (замкнутая ломаная), при условии, что никакие два звена ломаной не имеют общих точек, кроме концов соседних звеньев ломаной, называют многоугольником.
б) Звенья ломаной называют сторонами многоугольника, углы, составленные каждыми двумя соседними сторонами, — углами многоугольника, а эти вершины углов — вершинами многоугольника.
в) Сумму длин сторон многоугольника называют его периметром.
г) Многоугольник называют выпуклым, если он весь расположен по одну сторону от каждой прямой, содержащей его сторону.
д) Два многоугольника называют равными, если их можно совместить при наложении.
571. Постройте пятиугольник ABCDE. Назовите все его стороны и вершины.
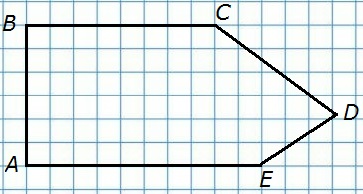
Стороны: AB, BC, CD, DE, EA.
Вершины: A, B, C, D, E.
572. Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. Например, в четырёхугольнике ABCD отрезка AC и BD — диагонали (рис. 119). Сколько диагоналей в выпуклом:
а) четырёхугольнике;
б) пятиугольнике;
в) шестиугольнике;
г) семиугольнике?
Пусть многоугольник имеет n вершин. Тогда из каждой вершины выходит (n — 3) диагоналей: 1 — сама вершина и 2 — соседние вершины.
Так как диагональ соединяет 2 вершины, значит необходимо (n — 3) разделить пополам и умножить на количество вершин, тогда мы получим, что количество диагоналей n-угольника равняется n • (n — 3) 2.
а) 4 • (4 — 3) 2 = 4 • 1 2 = 2 (диагонали) — в выпуклом четырёхугольнике;
б) 5 • (5 — 3) 2 = 5 • 2 2 = 10 2 = 5 (диагоналей) — в выпуклом пятиугольнике;
в) 6 • (6 — 3) 2 = 6 • 3 2 = 18 2 = 9 (диагоналей) — в выпуклом шестиугольнике;
г) 7 • (7 — 3) 2 = 7 • 4 2 = 28 2 = 14 (диагоналей) — в выпуклом семиугольнике.
573. Сколько диагоналей в выпуклом: а) десятиугольнике; б) двадцатиугольнике?
а) 10 • (10 — 3) 2 = 10 • 7 2 = 35 (диагоналей) — в выпуклом десятиугольнике;
б) 20 • (20 — 3) 2 = 20 • 17 2 = 170 (диагоналей) — в выпуклом двадцатиугольнике.
Исследуем
574. а) Исследуйте зависимость числа диагоналей (d) выпуклого многоугольника, выходящих из одной его вершины, от числа сторон этого многоугольника (n). Результаты занесите в таблицу.
б) Задайте формулой зависимость d от n.
а) Зависимость: (число диагоналей выпуклого многоугольника, выходящих из одной его вершины, на 3 меньше, чем сторон этого многоугольника)
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
б) d = n — 3.
575. а) Исследуйте зависимость числа диагоналей (d) выпуклого многоугольника от числа его сторон (n). Результаты занесите в таблицу.
б) Задайте формулой зависимость d от n.
а) Зависимость:
| n | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| d | 2 | 5 | 9 | 14 | 20 | 27 | 35 | 44 | 54 |
б) d = n • (n — 3) 2.
| ← Предыдущая | Следующая → |
Треугольный многоугольник
Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.
В зависимости от особенностей, фигура может называться:
Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.
Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.
Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Теорема об углах
Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.
Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.
Общие сведения
Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.
Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.
Любого вида многоугольник состоит из следующих частей:
Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.
Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.
Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.
Многоугольники
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :
В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.
Описание к рабочей тетради
Год: 2022.
Стандарт: ФГОС.
Издательство: Просвещение.
Издание (номер): 26-е издание, стереотипное.
Авторы: Атанасян Левон Сергеевич, Бутузов Валентин Федерович, Глазков Юрий Александрович, Юдина Ирина Игоревна.
ГДЗ (решебник) и ответы по Геометрии 7 класс. Рабочая тетрадь.
Гдз по геометрии 7 класс рабочая тетрадь Атанасян поможет выполнить любое задание, с которым возникла проблема. Тетрадь помогает лучше освоить и закрепить какие-либо темы, а решебник поможет понять и разобрать их. Здесь прописаны не только ответы, но и пояснения к ним. Так ученик будет не просто списывать, но и понимать, что к чему.
Кому будет полезно данное пособие:
- Семикласснику, который пропустил тему;
- Школьнику, который не понял чего-то на уроке, также может заглянуть сюда и увидеть пояснение к задачам;
- Родителю, который хочет помочь ребёнку;
- Репетитору, для подготовки определенный материалов;
- Учителю, для более быстрой проверки домашнего задания;
- Ребенку, который не хочет долго выполнять упражнения.
Таким образом можно понять, что такое пособие будет полезным абсолютно для всех, кто столкнулся с какими-то вопросами. Так можно сэкономить время, изучить тему, повторить её и узнать что-то новое.
Преимущества применения этого пособия:
Не придется думать, что это написано и почему так. Ниже ответа написано пояснение, с помощью которого можно что-то вспомнить или узнать.
Ответы исчерпывают себя, в них всё понятно изложено.
Какие-то построения или точки – всё это обозначено и имеется, также изложенные в ясном виде.
В итоге можно не только прояснить какие-то возникшие вопросы, но и улучшить свою успеваемость, а также развить в ребенке самостоятельность. Ведь ученик сам научится прорешивать упражнения, разбираться и анализировать их.
Необходимо помнить, что лучше всего попробовать выполнить задачу самостоятельно, а после обращаться к пособию. Онлайн решебник доступен и днём, и ночью, поэтому он всегда будет под рукой в нужный момент. При добросовестном и правильном использовании решебника, он станет верным помощником.
Ответы содержат подробные решения с пояснениями, а где-то задача визуализирована, для более понятного восприятия.
Также, не забывайте делиться домашкой сайта Отвечалка.су с друзьями и учитесь с нами на одни пятёрки!
Простейшие четырёхугольники
Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.
Наиболее часто приходится сталкиваться со следующими видами:
Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.
Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA
Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры
Вариации и обобщения
Планигон
См. также Теория и практика: Принадлежность точки многоугольнику • Теорема Бойяи — Гервина • Теорема Брахмагупты • Теорема Гаусса — Ванцеля • Формула Пика • Теорема о сумме углов многоугольника
Смотреть что такое «Многоугольник» в других словарях:
многоугольник — многоугольник … Орфографический словарь-справочник
МНОГОУГОЛЬНИК — (на плоскости) геометрическая фигура, ограниченная замкнутой ломаной линией, звенья которой называются сторонами многоугольника, а их концы вершинами многоугольника. По числу вершин различают треугольники, четырехугольники и т. д. Многоугольник… … Большой Энциклопедический словарь
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, плоская геометрическая фигура с тремя или более сторонами, пересекающимися в трех или более точках (вершинах). Они называются в соответствии с числом сторон или вершин: ТРЕУГОЛЬНИК (трехсторонний); ЧЕТЫРЕХУГОЛЬНИК… … Научно-технический энциклопедический словарь
многоугольник — полигон Словарь русских синонимов. многоугольник сущ., кол во синонимов: 12 • восьмиугольник (3) • … Словарь синонимов
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, многоугольника, муж. (мат.). Плоская фигура, ограниченная тремя, четырьмя и т.д. прямыми линиями. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
МНОГОУГОЛЬНИК — МНОГОУГОЛЬНИК, а, муж. В математике: геометрическая фигура, ограниченная замкнутой ломаной линией. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Многоугольник — Многоугольник. В элементарной геометрии М. называется фигура,ограниченная прямыми линиями, называемыми сторонами. Точки, в которыхстороны пересекаются, называются вершинами. Число вершин равняется числусторон. Смотря по этому числу, М. называются … Энциклопедия Брокгауза и Ефрона
многоугольник — (напр. сил) Тематики энергетика в целом EN polygon … Справочник технического переводчика
многоугольник — а; м. Геометрическая фигура, ограниченная ломаной линией, звенья которой образуют более четырёх углов. Правильный м. Сторона многоугольника. * * * многоугольник (на плоскости), геометрическая фигура, ограниченная замкнутой ломаной линией, звенья… … Энциклопедический словарь






























