Основные сведения о вычитании натуральных чисел

Вычитание натуральных чисел

читать материал украинским языком

Арифметическая операция вычитания чисел обозначается значком «минус» (-).

A - B = C

• А — уменьшаемое;
• В — вычитаемое;
• С — разность.

Разностью чисел А и В называется такое число С, которое надо прибавить к вычитаемому, чтобы получить уменьшаемое:

A - B = C;
В + С = А.

Складываются и вычитаются натуральные числа поразрядно, начиная с самого младшего разряда:

 255 808
+
 308 012
 -------
 563 820

Если при сложении двух цифр какого-либо разряда получается число, большее 9, то в сумму записывается только цифра, обозначающая разряд единиц, а «единичка» переходит в следующий разряд. Например, в приведенном выше примере при суммировании 8 и 2 получается 10 — в сумму заисывается 0, а 1 переходит в разряд десятков: 0+1+1 = 2. При суммировании 5 и 8 получается 13, поэтому в сумму (в разряд единиц тысяч) записывается 3, а 1 переходит в разряд десятков тысяч: 5+0+1 = 6.

 355 808
-
 308 012
 -------
  47 796

Если при вычитании приходится вычитать в соответствующем разряде большую цифру из меньшей, меньшая цифра «заимствует» единицу старшего разряда. Например, в нашем примере, при вычитании 0-1 (разряд десятков) ноль «занимает» единичку у разряда сотен (у восьмерки, стоящей левее), и становится не нулем, а 10, таким образом, мы вычитаем 1 не из нуля, а из 10 (получаем 9); теперь при вычитании разряда сотен мы будем отнимать 0 не от 8, а от 7, поскольку восьмерка «отдала» одну десятку в младший разряд. Аналогичная ситуация при вычитании 8 из 5: пятерка «занимает» десятку у пятерки, стоящей левее, и становится 15, теперь мы отнимаем 8 от 15 и получаем 7, после этого мы вычитаем 0 уже не от пятерки, а от четверки. Если в самом старшем разряде получается ноль, он не пишется.

Свойства разности натуральных чисел

Запишем основные правила, характеризующие свойства разности натуральных чисел:

• вычитание суммы из числа и числа из суммы;
• связь разности и изменения уменьшаемого или вычитаемого;
• вычитание разности из числа.

Разберем правило вычитания суммы из числа.

Алгоритм действий:

• вычислить разность данного числа и первого слагаемого;
• разность, которая получилась, уменьшить на второе слагаемое;
• повторить пункт второй с третьим и последующими слагаемыми.

Рассмотрим следующее правило вычитания натуральных чисел.

Алгоритм действий:

• поиск разности одного из слагаемых и данного числа;
• сложение полученного итога последовательно с каждым из слагаемых, которые остались.

Вспомним, что при изменении слагаемых закономерно меняется их сумма. Следующие свойства вычитания натуральных чисел являются следствиями записанного правила:

1. Увеличение уменьшаемого на определенное количество единиц приведет к увеличению разности на аналогичное количество единиц.
2. Уменьшение уменьшаемого на определенное количество единиц приведет к уменьшению разности на аналогичное количество единиц.
3. Увеличение вычитаемого на определенное количество единиц приведет к уменьшению разности на аналогичное количество единиц.
4. Уменьшение вычитаемого на определенное количество единиц приведет к увеличению разности на аналогичное количество единиц.
5. Увеличение или уменьшение одновременно уменьшаемого и вычитаемого на одинаковое количество единиц не изменит разность.

Запишем несколько способов вычитания разности.

Свойства сложения

1. Переместительное свойство (коммутативность):

   При перестановке слагаемых сумма не меняется

   $1 + 5 = 5 + 1 = 6.$

   В общем виде переместительное свойство записывается так:

   $a + b = b + a$.

2. Сочетательное свойство (ассоциативность):

   Сумма трех и более слагаемых не изменится, если изменить порядок их сложения

   $2 + ( 8 + 3 ) = ( 2 + 8 ) + 3 = 13.$

   В общем виде сочетательное свойство записывается так:

   $a + ( b + c ) = ( a + b ) + c.$

3. Свойство прибавления нуля:

   Если к числу прибавить нуль, то сумма будет равна самому числу

   $7 + 0 = 7.$

   К этому свойству можно применить переместительное свойство, получим:

   Если к нулю прибавить число, то сумма будет равна прибавляемому числу

   $0 + 7 = 7.$

   В общем виде:

   $a + 0 = 0 + a = a.$

   Если точкой $C$ разделить отрезок $AB$, то сумма длин отрезков $AC$ и $CB$ будет равна длине отрезка $AB$.

   Рисунок 2.

   Записывается: $AB = AC + CB$.

   Сложение чисел можно удобно выполнять «в столбик»:

   Рисунок 3.

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

Разность

Рассмотрим задачу. Велосипедист ехал из одной деревни в другую $2$ дня и проехал $64$ $км$. В первый день он проехал $33$ $км$, после чего остановился отдыхать до следующего дня. Сколько $км$ он проехал во второй день?

Рисунок $1$

Общее расстояние, которое проехал велосипедист, можно найти, сложив расстояние первого и второго дней. Таким образом, нам известна сумма и одно из слагаемых и нужно найти второе слагаемое.

То есть во второй день велосипедист проехал $64-33=31$ ($км$).

В рассмотренной задаче $64$ является уменьшаемым, $33$ — вычитаемым, а $31$ — разностью.

Рисунок $2$. Элементы вычитания

{"questions":,"answer":1}}}]}

Разберемся, как правильно прочитать разность$$\textcolor{green}{35-15}$$Это можно сделать несколькими способами:

• Из тридцати пяти вычесть пятнадцать.
• От тридцати пяти отнять пятнадцать.
• Разность тридцати пяти и пятнадцати.

{"questions":,"explanations":,"answer":},"image-2":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/05/vychitanie3.svg"}}}]}

Вычитание натуральных чисел

Вычитание — операция, обратная сложению.

Пример 2

На тарелке лежало $7$ яблок, съели $3$ яблока. Сколько яблок осталось на тарелке?

Очевидно, что если к оставшемуся числу яблок $(x)$ добавить $3$ яблока, то их станет $7$:

$x + 3 = 7.$

Таким образом, известно одно слагаемое и сумма, нужно найти второе слагаемое.

Для этого используется вычитание:

$x = 7 — 3 = 4$, т.к. $3 + 4 = 7.$

Число, из которого вычитают, называется уменьшаемым, а число, которое вычитают, — вычитаемым. Результат вычитания называется разностью.

Из данной задачи получаем:

$7$ — уменьшаемое, $3$ — вычитаемое, $8$ — разность.

В общем виде

Если $b + c = a$, то

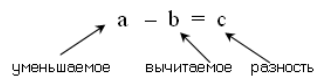Рисунок 4.

При вычитании натуральных чисел уменьшаемое обязательно должно быть больше вычитаемого:

$11 — 3 = 8; 8 > 3.$

Разность двух чисел находят, чтобы узнать на сколько уменьшаемое больше вычитаемого или на сколько вычитаемое меньше уменьшаемого:

$11$ больше $3$ на $8$.

Вычитание многозначных чисел в столбик

До этого на примерах были рассмотрены простые задачи на вычитание натуральных чисел. Познакомимся с методом вычитания в столбик многозначных чисел. Данный способ существенно упрощает расчеты.

В качестве примера попробуем найти значение следующего выражения:

50063 – 4825

Далее начнем вычитать единицы из единиц, десятки из десятков и так далее. Заметим, что число 3 меньше по сравнению с числом 5, поэтому разложим число 6 и получим 5 десятков и 1 десяток. В 1 десятке 10 единиц, которые следует прибавить к 3 единицам. Из полученной суммы 13 вычитаем 5. Полученные 8 единиц запишем внизу под числом 5.

Затем можно приступить к вычитанию десятков:

При вычитании сотен следует руководствоваться тем же алгоритмом, что и при вычитании единиц. Займем необходимое количество единиц и выполним вычитание:

Продолжим выполнять арифметические действия с учетом позаимствованных единиц:

Таким образом:

50063 − 4825 = 45238

При необходимости выполненные расчеты можно проверить с помощью сложения. Вспомним, что для проверки сложения требуется поменять местами слагаемые и суммировать их повторно. Рассмотрим пример:

5728+803 = 6531

Сложение можно проверить с помощью вычитания. Для этого необходимо полученную сумму уменьшить на какое-то из слагаемых. При правильном расчете результат должен быть равен второму слагаемому.

Вычитание допустимо проверить с помощью сложения. Если прибавить вычитаемое к остатку, то получим уменьшаемое. Тогда можно сделать вывод о корректности выполненных вычислений.

50063 − 4825 = 45238

Другим способом проверки вычитания является вычитание. Если уменьшить уменьшаемое на остаток, то в результате должно получиться вычитаемое.

Сложение

Как представить себе сложение? Проще всего представить каждое число в виде единиц или каких-нибудь вещей. В начальной школе дети складывают фрукты, потому что их проще всего себе представить. В математике средней школы сложение представляют как движение числа по числовой прямой вправо, то есть по направлению движения.

Направлением движения числовой прямой называют направление вдоль прямой, по которому происходит увеличение числа. Например, число 15 дальше числа 3 по направлению движения числовой прямой

При понимании сути операции сложение не вызывает затруднений. Но они возникают при сложении положительного числа с отрицательным, поэтому запишем общий алгоритм для сложения любых чисел, кроме иррациональных.

• Первый шаг это определение категорий чисел. Нужно понять, что за числа перед нами: два отрицательных, или одно отрицательное и одно положительное? Для каждого из случаев есть свой порядок выполнения действий.
• Если перед вами два положительных числа, то нужно просто сложить их без особых действий. Если вы складываете большие числа или не уверены в правильности ответа, то нужно выполнить проверку. Для этого из результата вычитают первое слагаемое. При правильном решении, результат проверки будет равен второму слагаемому. Если перед вами не две положительных числа, то нужно переходить к следующему пункту без выполнения сложения.
• Если складывается положительное и отрицательное число, то сложение нужно заменить разностью. То есть из положительного вычесть число, по модулю равное отрицательному. Будьте внимательны, результатом может быть. Как положительное число, так и ноль или отрицательное число. Если перед нами два отрицательных числа сразу же переходим к следующему пункту без выполнения каких-либо действий.
• Если складываются два отрицательных числа, то числа преобразуются в положительные. После выполняется сложение, а потом числу возвращается знак минус. Для того, чтобы пример был правильным в записи знак минус просто выносят за скобки. Чтобы не допускать ошибок, на первых порах можно выносить за скобки число -1

Вот и весь алгоритм.

Вычитание на координатном луче

Решим пример $\textcolor{green}{8}-\textcolor{lightblue}{3}$ на координатном луче.Начертим координатный луч и отметим $\textcolor{green}{уменьшаемое}$ число $\textcolor{green}{8}$:

Затем сделаем влево количество шагов равное $\textcolor{lightblue}{вычитаемому}$ $\textcolor{lightblue}{3}$:

Получаем $8-3=\textcolor{purple}{5}$.

{"questions":,"answer":}},"hints":[]}]}

Вычитание суммы из числа

Если необходимо вычесть из одного числа сумму двух других чисел, например:$$85-(25+16)$$

Тогда на помощь приходит свойство вычитания суммы из числа:

Не зная этого свойства, мы бы вычисляли так: $$85-\textcolor{red}{(25+16)}=85-\textcolor{red}{41}=44$$

Но если использовать свойство вычитания суммы из числа, то решение выглядит так: $$85-(\textcolor{blue}{25}+16)=(85-\textcolor{blue}{25})-16=60-16=44$$

Результат не меняется, но с использованием свойства вычитания суммы из числа вычисления могут быть проще.

{"questions":,"answer":0}},"step":1,"hints":}]}

Запишем данное правило в буквенном виде:$$\textcolor{blue}{a}-(\textcolor{orange}{b}+\textcolor{darkgreen}{c})=(\textcolor{blue}{a}-\textcolor{orange}{b})-\textcolor{darkgreen}{c}$$

Вычитание числа из суммы

Бывает, что требуется вычесть число из суммы двух других чисел:$$(68+12)-33$$

Данное свойство применимо, когда слагаемое, из которого вычитают число, больше этого числа, либо равно ему.

{"questions":,"answer":0}},"step":1,"hints":}]}

В том случае, когда оба слагаемых суммы меньше вычитаемого из суммы числа, то воспользоваться свойством не получится, поэтому придется выполнять действия по порядку.

{"questions":,"answer":0}},"step":1,"hints":}]}

Запишем данное правило в буквенном виде:$$(\textcolor{blue}{a}+\textcolor{orange}{b})-\textcolor{darkgreen}{c}=(\textcolor{blue}{a}-\textcolor{darkgreen}{c})+\textcolor{orange}{b}$$

Вычитание нуля

Например, у нас есть $6$ яблок. Если мы отнимем от этого количества $0$, получается, мы ничего не отнимем, и количество яблок не уменьшится.

Рисунок $4$

Запишем данное правило в буквенном виде:$$\textcolor{orange}{b-0=b}$$

{"questions":,"answer":0}},"hints":}]}

Вычитание из числа самого себя

Возьмем наш пример с шестью яблоками. Если мы вычтем (например, съедим) из этого количества $6$ штук, яблок не останется.

Рисунок $5$

Запишем данное правило в буквенном виде:$$\textcolor{orange}{b-b=0}$$

{"questions":,"answer":}},"hints":[]},{"content":"Дан пример $(63+29)-43$. Какое действие нужно выполнить первым, чтобы воспользоваться свойством вычитания числа из суммы?`choice-8`","widgets":{"choice-8":{"type":"choice","options":,"answer":}},"hints":[]},{"content":"Вычислите $15-0$`choice-18`","widgets":{"choice-18":{"type":"choice","options":,"answer":}},"hints":[]},{"content":"Вычислите $38-38$`choice-23`","widgets":{"choice-23":{"type":"choice","options":,"answer":}},"hints":[]}]}

Ответы к заданию Применяем математику на страницах 42 и 43

Другие решебники 5 класс:

• Математика
• Русский язык
• История

1. У Миши с Сашей было 3 купюры по 200 р. Они купили 3 пакета пряников по 81 р. Затем купили на сдачу мороженое по 60 р.
а) Сколько купюр они дали продавцу при покупке пряников? Сколько получили рублей сдачи?
3 * 81 = 243 (р.) — стоимость пряников
Ребята дали продавцу 2 купюры по 200 р.
2 * 200 — 243 = 400 — 243 = 157 (р.) — сдача

б) Сколько пачек мороженого смогли купить?
На сдачу ребята купили два мороженых: 2 * 60 = 120 р.

в) Сколько денег осталось после всех покупок?
200 + 157 — 120 = 200 + 37 = 237 (p.) — сдача после всех покупок

2.

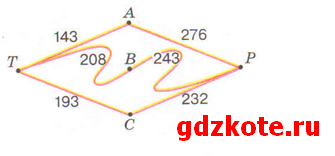
а) Определите по схеме (рис. 1.45) самый короткий путь из пункта Т в пункт Р, запишите его длину. На схеме расстояния указаны в километрах.
Путь ТАР: 143 + 276 = 419 (км) — самый короткий путь
Путь ТВР: 208 + 243 = 451 (км)
Путь TCP: 193 + 232 = 425 (км)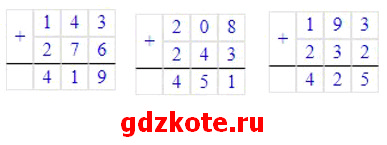

б) Хватит ли водителю 40 л бензина для поездки из пункта Т в пункт P, если расход бензина на 100 км равен 10 л?
Так как на 100 км расход бензина равен 10 л, то 40 л хватит на 40 * 10 = 400 (км).
400 < 419, значит 40 л не хватит для поездки из пункта Т в пункт Р.

3. Для изготовления поделки Лёше надо отмерить полоски бумаги, ширина которых равна 3 см, 4 см, 2 см, 5 см. Сможет ли он это сделать, если на старой линейке остались только деления 0, 7 и 10?Чтобы изготовить полоску шириной 3 см, можно воспользоваться расстоянием по линейке от деления 7 до деления 10.Чтобы изготовить полоску шириной 4 см, можно от деления 7 на линейке отложить 3 см от полоски в 3 см.Чтобы изготовить полоску шириной 2 см, нужно отложить 3 отрезка по 10 см, а затем в обратную строну отложить 4 отрезка по 7 см: 3 * 10 — 4 * 7 = 30 — 28 = 2.Чтобы изготовить полоску шириной 5 см, нужно отложить 5 отрезков по 7 см, а затем в обратную строну отложить 3 отрезка по 10 см: 5 * 7 — 3 * 10 = 35 — 30 = 5.

4. Таня подошла к табло в аэропорту в 16:30, чтобы узнать информацию о вылете в Симферополь рейсом 309.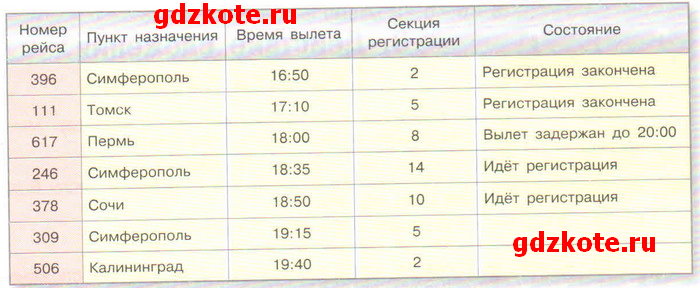

а) Сколько времени осталось до регистрации, если регистрация начинается за два с половиной часа до вылета?
19 ч 15 мин — 2 ч 30 мин = 18 ч 75 мин — 2 ч 30 мин = 16 ч 45 мин — в это время начинается регистрация.
16 ч 45 мин — 16 ч 30 мин = 15 мин — осталось до регистрации.

б) Сколько рейсов на Симферополь показано на табло?3 рейса на Симферополь: 396, 246, 309.

в) Сколько времени осталось до вылета в Симферополь предыдущего рейса?
18 ч 35 мин — 16 ч 30 мин = 2 ч 5 мин.

г) В какой секции будет регистрация на Танин рейс?
В 5 секции.

д) Идёт ли там регистрация на другой рейс?Нет, не идет (регистрация закончилась).

5. Утки могут летать на высоте до 800 м, аист — до 900 м, ласточки — до 2000 м, а орлы — до 3000 м. Представьте эту информацию в виде столбчатой диаграммы.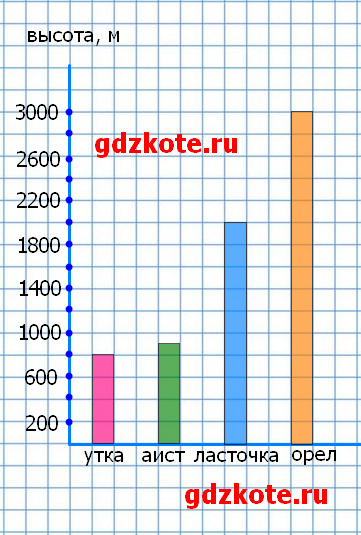

6. На сковороде можно одновременно жарить 2 оладушка. Для обжаривания одной стороны требуется 20 с. За какое наименьшее время можно приготовить 3 оладушка? Для решения используйте таблицу.

Время, с	Первый оладушек	Второй оладушек	Третий оладушек
1-20	+	+	—
21-40	+	—	+
41-60	—	+	+

Сначала жарим два оладушка с одной стороны. Затем второй оладушке убираем и заливаем третий, а первый переворачиваем. Далее убираем первый готовый оладушек, третий оладушек переворачиваем, а второй добавляем для обжаривания со второй стороны. Затем убираем второй и третий оладушки.
В итоге получаем, что для приготовить 3 оладушков нужно потратить 60 секунд (1 минута).

• ← предыдущее
• следующее →