Занимательные квадраты для младших школьников 2 класса. Решения. Примеры
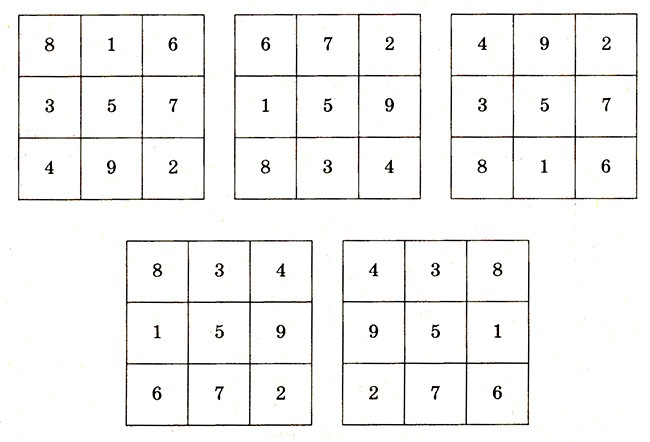
1. Для составления занимательных квадратов подбирают 9 таких чисел, чтобы разность между соседними числами была равна постоянному числу. Например:
1, 3, 5, 7, 9, 11, 13, 15, 17.
В этом ряду подчеркивают вторую тройку чисел. Сложив эти числа, получают сумму занимательного квадрата (7 + 9 + 11 = 27). Эту тройку чисел располагают по любой диагонали. Рядом с наименьшим числом (7) располагают самое большое число в ряду (17), либо самое меньшее число ряда (1) помещают рядом с самым большим из трех подчеркнутых (11).

Учащиеся, производя действия, заполняют все клетки в 1-м квадрате. Например:
7 + 17 = 24 27 — 24 = 3
11 + 3 = 14 27 – 14 = 13
13 + 9 = 22 27 — 22 = 5
7 + 5 = 12 27-12= 15
15 + 11 = 26 27- 26 = 1
Аналогично заполняется 2-й квадрат. Данные квадраты можно заменить другими, увеличив каждое число в квадрате на несколько единиц.
2. Заполните все клетки числами так, чтобы при сложении чисел по всем направлениям получилось число 90.
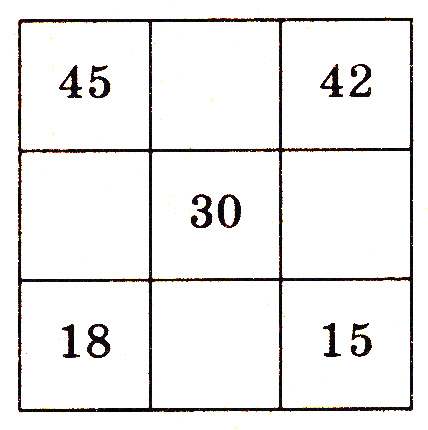
Второй способ составления магических квадратов состоит в следующем.
Чтобы составить занимательный квадрат, надо взять число, которое делится на 3. Например, сумма равна 30. При составлении занимательного квадрата учителю достаточно воспользоваться следующим правилом: пусть s, m, k — целые числа, причем m + k < s/3. Например: s = 30, тогда s/3 = 10. Для m и k можно взять числа 4 и 3, так как 4 + 3 < 10. Находим, что s/3 + m = 10 + 4 = 14, s/3 — m = 10 — 4 = 6, s/3 + k = 10 + 3 = 13, s/3 — k = 10 — 3 = 7, после чего по формулам заполняют остальные клетки.
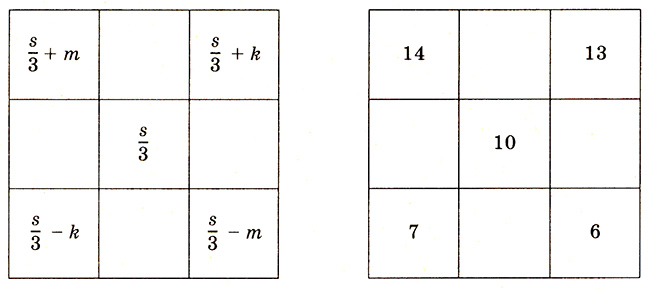
(Этот способ составления занимательного квадрата предлагается для учителя.)
3. Для разнообразия подобные головоломки можно составлять не только в виде квадратов, но и фигур иной формы: круга, треугольника, звезды и т. п.
Например:
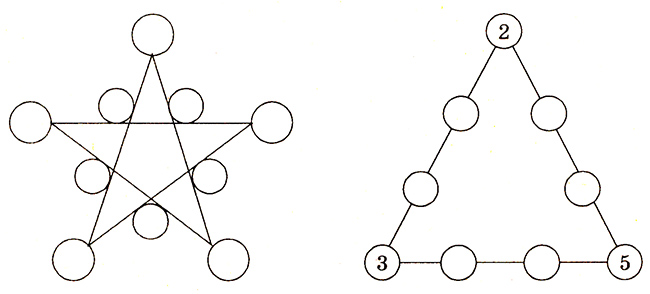
В кружках треугольника размещают числа от 1 до 9 с общей суммой 20.
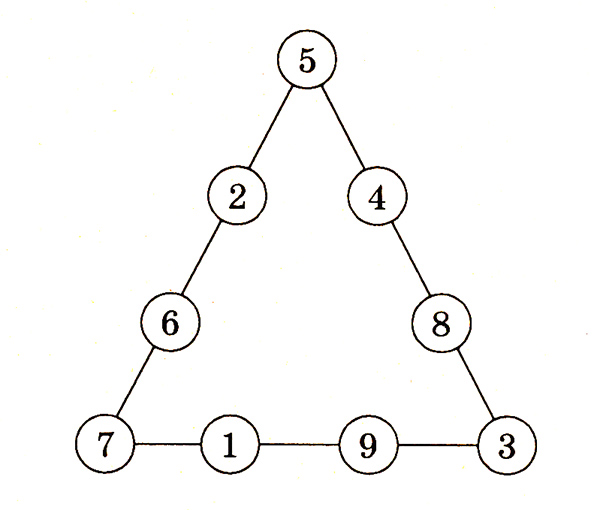
4. В кружках этого треугольника расставить все 9 значащих цифр так, чтобы сумма их на каждой стороне составляла 20.
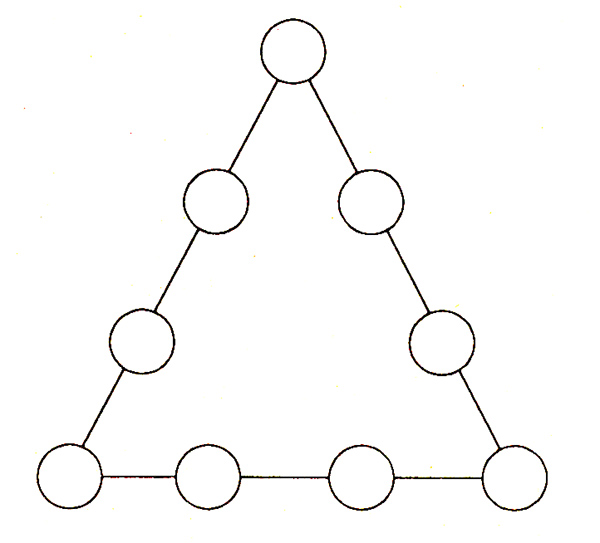
5. Все значащие цифры разместить в кружках того же треугольника так, чтобы сумма их на каждой стороне равнялась 17.
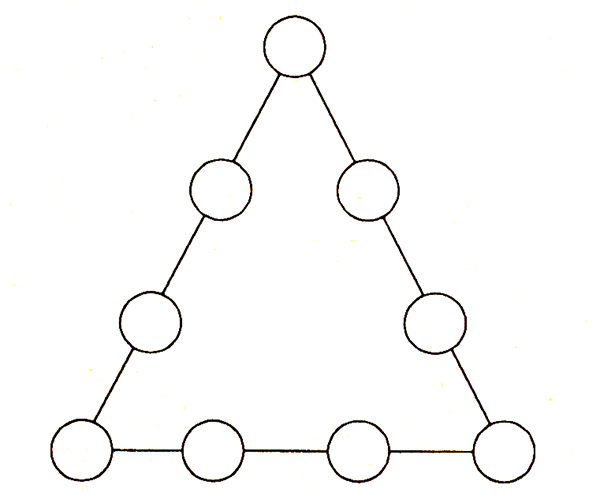
6. На девяти кружках игрового поля надо разложить карточки с цифрами от 1 до 9 так, чтобы числа в кружках, расположенных на одной линии, составили в сумме число 15.
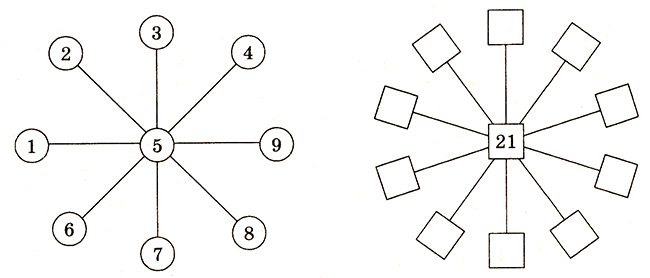
7. Расставить числа в квадратиках таким образом, чтобы сумма любых трех чисел, связанных прямой линией, составляла 42.
8. В кружках этой фигуры расставить недостающие числа от 1 до 21 так, чтобы сумма чисел в каждой из трех окружностей была равна 60. Числа на окружностях не должны повторяться.
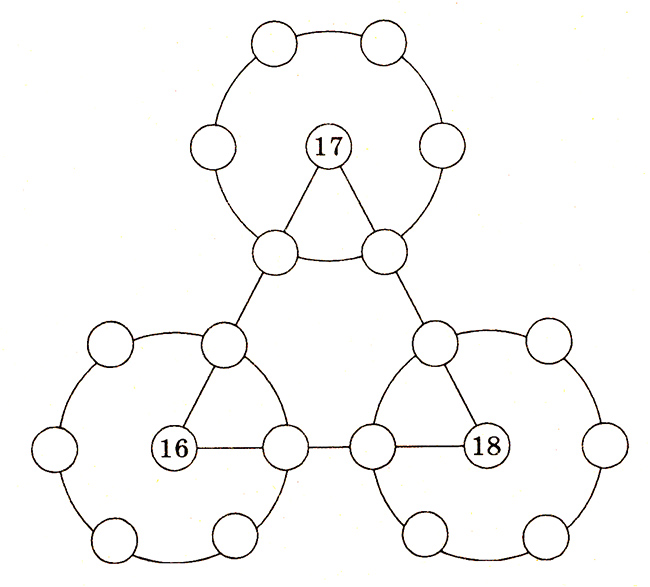
Вот один из способов решения этой головоломки.
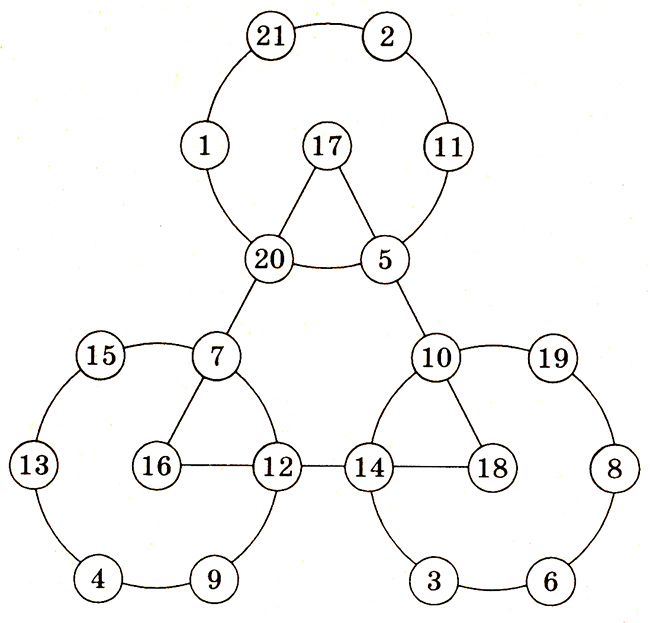
Найдите другие способы решения головоломки.
9. Разместить числа от 1 до 12 (по одному числу в каждой фигуре) так, чтобы они составляли одну и ту же сумму в следующих направлениях: в каждой из двух центральных колонок; в каждом из двух центральных рядов; в четырех кружках вместе, в четырех треугольниках вместе, в четырех квадратах вместе (результат — см. рис.).
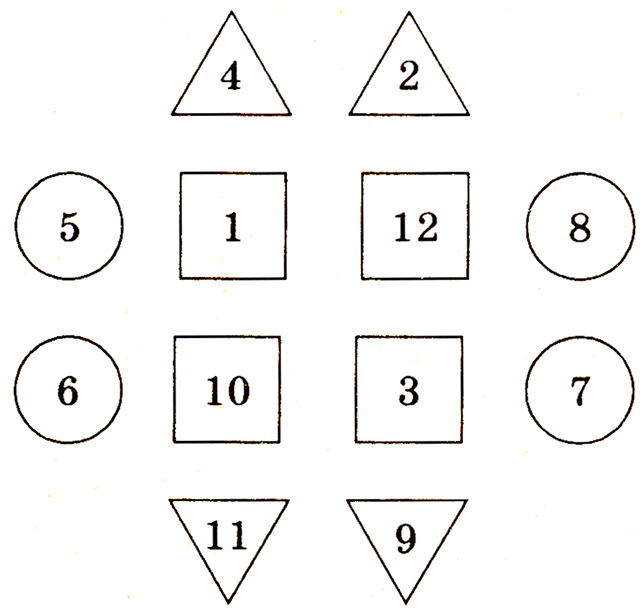
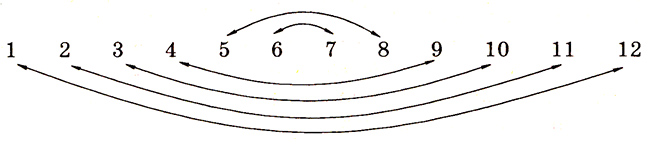
Перед заполнением фигур числами вспомните игру «Числа, бегущие навстречу друг другу».
В каждом направлении разместите четыре числа, указанных стрелками.
10. Третий способ составления магических квадратов.
Составив один магический квадрат, легко получить его видоизменения, то есть найти ряд новых магических квадратов. Если, например, мы составили квадрат, то, повернув его мысленно на четверть оборота, получаем другой магический квадрат.

Дальнейшие повороты на 120° дадут еще два видоизменения начального квадрата.
Каждый из вновь полученных магических квадратов можно, в свою очередь, видоизменить, если представить себе, что он как бы отражен в зеркале.
11. Четвертый способ составления занимательных квадратов — способ Баше. Он предложен французским математиком и назван его именем.
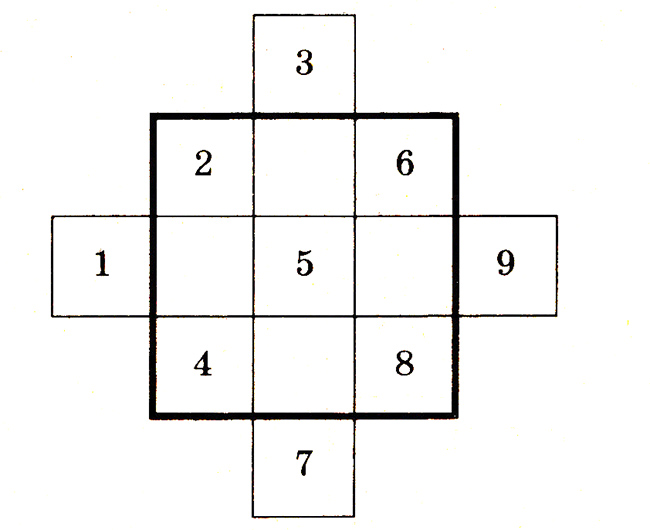
В квадрат, разграфленный на 9 клеток, надо вписать по порядку числа от 1 до 9, располагая их косыми рядами по 3 в ряд, как показано на рисунке.
Числа, стоящие вне квадрата, вписать внутрь его так, чтобы они примкнули к противолежащим сторонам квадрата (оставаясь в тех же столбиках или строках, что и раньше).
В результате получается квадрат:

12. Проделав с квадратом из девяти клеток все повороты и отражения, получаем следующие его видоизменения: