Как делить в столбик? как объяснить ребенку деление столбиком? деление на однозначное, двузначное, трехзначное число, деление с остатком

Часть 2:

стр. 4

стр. 5

стр. 6

стр. 7

стр. 8

стр. 9

стр. 10

стр. 11

стр. 12

стр. 13

стр. 14

стр. 15

стр. 16

стр. 17

стр. 18

стр. 19

стр. 20

стр. 21

стр. 22

стр. 23

стр. 24

стр. 25

стр. 26

стр. 27

стр. 28

стр. 29

стр. 30

стр. 31

стр. 32

стр. 33

стр. 34

стр. 35

стр. 36

стр. 37

стр. 38

стр. 39

стр. 40

стр. 41

стр. 42

стр. 43

стр. 44

стр. 45

стр. 46

стр. 47

стр. 48

стр. 49

стр. 50

стр. 51

стр. 52

стр. 53

стр. 54

стр. 55

стр. 56

стр. 57

стр. 58

стр. 59

стр. 60

стр. 61

стр. 62

стр. 63

стр. 64

стр. 65

стр. 66

стр. 67

стр. 68

стр. 69

стр. 70

стр. 71

стр. 72

стр. 73

стр. 74

стр. 75

стр. 76

стр. 77

стр. 78

стр. 79

стр. 80

стр. 81

стр. 82

стр. 83

стр. 84

стр. 85

стр. 86

стр. 87

стр. 88

стр. 89

стр. 90

стр. 91

стр. 92

стр. 93

стр. 94

стр. 95

стр. 96

стр. 97

стр. 98

стр. 99

стр. 100

стр. 101

стр. 102

стр. 103

стр. 104

стр. 105

стр. 106

стр. 107

стр. 108

стр. 109

стр. 110

стр. 111

стр. 112

стр. 113

стр. 115

стр. 116

Ответы к стр. 36

137. Какие законы используют при умножении столбиком?

Законы сложения и умножения: α + 0 = α, α • 0 = 0, α • 1 = α, таблица умножения.

138. Объясните, как выполнено умножение:

а) _×748    б) _×973    в) _×7050         6              50           7      4488        48650      49350    

г) _×926    д) _×326      е) _×4830       38          502              4900 ₊ 7408    ₊      652       ₊ 4347 2778       1630           1932         35188     163652        23667000    

а) Умножение трёхзначного числа на однозначное.
б) Так как 973 • 50 = 973 • 5 • 10, то можно сначала умножить 973 на 5, а затем полученный результат умножить на 10, то есть приписать к нему справа нуль. Поэтому 5 пишем под 3, а ноль приписываем справа.
в) Так как 7050 • 7 = 705 • 10 • 7, то можно сначала умножить 705 на 7, а затем полученный результат умножить на 10, то есть приписать к нему справа нуль. Поэтому 7 пишем под 5, а ноль приписываем справа.
г) Умножение трёхзначного числа на двухзначное.
д) Число 502 содержит цифру 0 при умножении на которую числа 326 получается 0. Поэтому эту строку в вычислениях можно опустить, а значение произведения 326 на 5 начать записывать справа налево под цифрой 5.е) Так как 4830 • 4900 = 483 • 10 • 49 • 100 = 483 • 49 • 1000, то можно сначала умножить 483 на 49, а затем полученный результат умножить на 1000, то есть приписать к нему справа три нуля. Поэтому 9 пишем под 3, а нули приписываем справа.

139. Вычислите произведение чисел:
а) 12 • 10;       б) 32 • 100;        в) 65 • 1000;
г) 20 • 100;      д) 300 • 1000;   е) 1500 • 100;
ж) 10 • 190;     з) 1000 • 20;      и) 100 • 380;
к) 129 • 100;   л) 1000 • 130;    м) 2900 • 10.

а) 12 • 10 = 120;
б) 32 • 100 = 3200;
в) 65 • 1000 = 65 000;
г) 20 • 100 = 2000;
д) 300 • 1000 = 300 000;
е) 1500 • 100 = 150 000;
ж) 10 • 190 = 1900;
з) 1000 • 20 = 20 000;
и) 100 • 380 = 38 000;
к) 129 • 100 = 12 900;
л) 1000 • 130 = 130 000;
м) 2900 • 10 = 29 000.

140. Вычислите произведение чисел:
а) 24 • 2;   б) 31 • 3;   в) 52 • 4;   г) 71 • 9;
д) 23 • 8;  е) 9 • 18;   ж) 65 • 4;   з) 76 • 5;
и) 48 • 9;  к) 8 • 34;   л) 7 • 85;   м) 9 • 78.

а) 24 • 2 = (20 + 4) • 2 = 20 • 2 + 4 • 2 = 40 + 8 = 48;
б) 31 • 3 = (31 + 1) • 3 = 30 • 3 + 1 • 3 = 90 + 3 = 93;
в) 52 • 4 = (50 + 2) • 4 = 50 • 4 + 2 • 4 = 200 + 8 = 208;
г) 71 • 9 = (70 + 1) • 9 = 70 • 9 + 1 • 9 = 630 + 9 = 639;
д) 23 • 8 = (20 + 3) • 8 = 20 • 8 + 3 • 8 = 160 + 24 = 184;
е) 9 • 18 = 9 • (10 + = 9 • 10 + 9 • 8 = 90 + 72 = 162;
ж) 65 • 4 = (60 + 5) • 4 = 60 • 4 + 5 • 4 = 240 + 20 = 260;
з) 76 • 5 = (70 + 6) • 5 = 70 • 5 + 6 • 5 = 350 + 30 = 308;
и) 48 • 9 = (40 + • 9 = 40 • 9 + 8 • 9 = 360 + 72 = 432;
к) 8 • 34 = 8 • (30 + 4) = 8 • 30 + 8 • 4 = 240 + 32 = 272;
л) 7 • 85 = 7 • (80 + 5) = 7 • 80 + 7 • 5 = 560 + 35 = 595;
м) 9 • 78 = 9 • (70 + = 9 • 70 + 9 • 8 = 630 + 72 = 702.

141. Вычислите произведение чисел:
а) 132 • 5;       б) 645 • 3;       в) 5 • 418;        г) 7 • 338;
д) 106 • 4;       е) 401 • 6;       ж) 4381 • 2;     з) 7713 • 8;
и) 7 • 6204;     к) 9 • 5007;     л) 6 • 5769;      м) 7 • 777.

а) _×132     б) _×645     в) _×418     г) _×338         5               3              5              7     660          1935         2090        2366

д) _×106     е) _×401   ж) _×4381   з) _×7713         4               6              2              8     424          2406         8762      61704

и) _×6204   к) _×5007   л) _×5769   м) _×777           7              9              6             7    43428       45063       34614       5439

142. Вычислите произведение чисел:
а) 23 • 11;   б) 42 • 12;   в) 22 • 33;
г) 53 • 31;   д) 68 • 61;   е) 64 • 24;
ж) 79 • 23;  з) 72 • 25;   и) 42 • 68;
к) 37 • 33;   л) 74 • 15;   м) 37 • 66;
н) 48 • 37;   о) 54 • 29;   п) 63 • 36.

а)  _×23    б) _×42      в) _×22       11          12           33     ₊ 23        ₊ 84        ₊ 66    23           42          66    253         504         726    

г)  _×53    д) _×68      е) _×64       31         61            24     ₊ 53       ₊ 68        ₊ 256   159       408           128       1643      4148         1536  

ж)  _×79    з) _×72      и) _×42       23          25            68   ₊ 237      ₊ 360        ₊ 336   158        144           252      1817      1800         2856  

к)  _×37    л) _×74      м) _×37       33         15            66   ₊ 111      ₊ 370       ₊ 222   111          74          222      1221       1110       2442  

н)  _×48    о) _×54      п) _×63       37          29            36   ₊ 336      ₊ 486        ₊ 378   144        108           189      1776      1566         2268  

143. Вычислите произведение чисел:
а) 86 • 49;       б) 92 • 16;        в) 88 • 97;
г) 951 • 18;      д) 663 • 26;     е) 847 • 64;
ж) 101 • 332;   з) 302 • 648;   и) 321 • 562;
к) 955 • 317;    л) 861 • 242;   м) 999 • 732;
н) 679 • 679;    о) 125 • 125;   п) 420 • 450.

а)  _×86    б) _×92      в) _×88       49          16           97   ₊ 774      ₊ 552       ₊ 616   344          92          792      4214        1472       8536    

г)  _×951    д) _×663      е) _×847        18            26             64  ₊ 7608      ₊ 3978       ₊ 3388    951        1326          5082      17118      17238         54208  

ж)  _×332    з) _×648      и) _×321       101          302            562  ₊     332      ₊ 1296          642   332         1944        +1926      33532     195696     1605                                     180402

к)  _×955    л) _×861      м) _×999       317         242            7326685      1722          1998   +955    +3444         +2997    2865       1722         6993      302735    208362     731268

н)     _×679    о) _×125      п) _×420       679         125            4506111        625         ₊210 +4753      +250           168 4074         125             189000 461041     15625     

144. Вычислите наиболее простым способом:
а) 24 • 98 + 24 • 2;     б) 305 • 199 + 305 • 1;
в) 49 • 18 + 18;          г) 153 • 598 + 306.

а) 24 • 98 + 24 • 2 = 24 • (98 + 2) = 24 • 100 = 2400;
б) 305 • 199 + 305 • 1 = 305 • (199 + 1) = 305 • 200 = 61 000;
в) 49 • 18 + 18 = (49 + 1) • 18 = 50 • 18 = 900;
г) 153 • 598 + 306 = 153 • 598 + 153 • 2 = 153 • (598 + 2) = 153 • 600 = 91 800.

145. Выполните действие:а) 325 • 40;      б) 3508 • 250;   в) 7380 • 420;г) 3800 • 550;   д) 48 • 9;           е) 789 • 1020.

а)  _×325    б) _×3508      в) _×7380          40            250            420    13000     ₊17540        ₊ 1476                    7016          2952                          877000      3099600

г)  _×3800      д) _×48      е) _×789      550                9            1020   ₊190             432         ₊1578  190                              789         2090000                       804780

← Предыдущая

Следующая →

Как научиться делить столбиком

Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:

• Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
• Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
• Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
• Решать маленькие задачи на умножение, разность, сумму устно.

Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:

6х2=12

6х3=18

6х4=24 и так далее.

Смело предлагайте такие примеры:

24:6=4

24:4=6

12:2=6

18:3=6

Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.

Игровые задания

Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.

• Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.

  Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.

• Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
• «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.
• «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
• Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.

• «Ищем дерево».

  Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:

45:9           120:60          14:7

Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:

45:9=5

120:60=2

14:7=2

5+2+2=9

Ребенок должен найти дерево под номером 9.

Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.

После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.

Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:

1. Мама-учитель

Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.

Например, это:

Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.

3. Нанять репетитора

Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом.

Этот вариант оставим на крайний случай.

Как делить столбиком десятичные дроби с запятой?

Существует несколько особенностей при подобном делении. Если вы совершаете действие с:

• десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
• числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя. Например, 749,5:100=7,495,
• десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.

Как пошагово объяснить алгоритм математического действия?

Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:

Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части

Важно указать ребенку, что ответ не должен превышать 9.
Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
Далее, нужно найти разницу между частью делимого и полученным произведением.
Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.

Деление многозначного числа на многозначное

При делении многозначного числа на многозначное поступаем точно так же, как поступали при делении многозначного числа на однозначное.

Разделяя число 37207 на 47, мы прежде всего определяем, из скольких цифр состоит частное. Частное меньше 1000 и больше 100, ибо 37207 меньше 47000 (47 × 1000) и больше 4700 (47 × 100), следовательно, частное состоит из сотен, десятков и единиц. Начиная с сотен, мы определяем каждую цифру частного отдельно:

1. Определяем сотни частного:

   Делимое 37207 имеет 372 сотни. Десятки и единицы делимого не имеют влияния на цифру сотен частного. В частном может быть только 7 сотен, ибо 47 содержится в 372 семь раз; пишем в частном 700.

   Умножая делитель на частное и вычитая из делимого, получаем первый остаток 4307.

2. Определяем десятки частного:

   Остаток 4307 содержит 430 десятков. Единицы не имеют влияния на цифру десятков частного. Делитель 47 содержится в 430 девять раз; пишем в частном 90.

   Умножая 90 на частное 47 и вычитая произведение 4330, получаем в остатке 77.

3. Определяем единицы частного:

   47 содержится в 77 один раз. Пишем в частном 1 и, вычитая из 77 произведение единицы на делитель, получаем в остатке 30.

Итак, после деления имеем в целом частном 791 и в остатке 30.

Если не писать каждый раз лишних нулей и принимать в соображение только те цифры делимого, которые имеют влияние на частное, ход вычисления изобразится письменно:

словесно:

1. Отделяем в делимом от левой руки к правой столько цифр, чтобы делитель мог содержаться в отделенной части делимого. В данном случае отделяем 3 цифры, 47 содержится в 372 семь раз; умножаем делитель 47 на 7, цифру частного, и, вычитая произведение 47 × 7 = 329 из 372, получаем в остатке 43.

   

   

   

   

   

   

   

   

   

   

2. К остатку 43 сносим 0, следующую цифру делимого; 47 содержится в 430 девять раз, пишем в частном 9. Умножая 47 на 9 и вычитая произведение 423 из 430, получаем остаток 7.

3. Сносим к остатку следующую цифру частного 7; 47 содержится в 77 один раз. Пишем единицу в частном.

Умножая ею делитель и вычитая 47 из 77, получаем в остатке 30 и в целом частно 791.

Пример. Разделить 671064 на 335. Деление изобразится письменно:

словесно:

1. Отделяем 671 в делимом; 335 содержится в 671 два раза, пишем в частном 2. Умножая 335 на 2 и вычитая произведение 670, получим в остатке 1.

2. Сносим 0, следующую цифру делимого; 335 не содержится в 10, — пишем для второй цифры частного 0.

3. Сносим 6, следующую цифру делимого; 335 не содержится в 106, — пишем для третьей цифры частного 0.

4. Сносим следующую цифру делимого 4; 335 содержится в 1064 три раза, — пишем в частном 3. Умножая делитель на 3 и вычитая произведение, получим в остатке 59 и в целом частном 2003.

Из предложенных примеров выводим следующее правило:

1. Чтобы разделить многозначное число на однозначное или многозначное, нужно отделить в делимом от левой руки к правой столько цифр, сколько их находится в делителе. Если делитель не содержится, отделяют в делимом одной цифрой больше. Разделив отделенное число на делитель, получают первую цифру частного, умножают ей делитель и полученное произведение вычитают из отделенной части делимого.

2. К остатку сносят следующую цифру делимого и снова задаются.

3. Если при этом получается число меньше делителя, пишут в частном нуль, сносят следующую цифру и снова задаются.

4. Получив новую цифру частного, поступают с нею так же, как и с первой цифрой.

5. Деление продолжают до тех пор, пока не снесут всех цифр делимого и не получат таким образом всех цифр частного.

Всякий раз, когда приходится делить, нужно задаваться в частном такою цифрой, чтобы остаток был меньше делителя

Чтобы легче найти такую цифру частного, при делении многозначного числа на многозначное обращают внимание на одну или две старшие цифры делителя и задаются только ими в соответствующей части делимого. При этом в делимом и в делителе отделяют от правой руки к левой одинаковое число цифр

Так, определяя, сколько раз содержится 6373 в 27302, мы задаемся четырьмя, ибо 6 в 27 содержится 4 раза.

Полученная при этом цифра частного будет или равна или больше действительной. В последнем случае ее нужно уменьшить.

Иногда при делении не подписывают произведение цифры частного на делитель, а, подразумевая его в уме, подписывают один остаток. Сокращая таким образом деление, изображают его письменно:

словесно:

1. 8 в 43 содержится 5 раз; 5-ю 8 — сорок. Вычитая 40 из 43, получаем в остатке 3.

2. Сносим 2; 8 в 32 содержится 4 раза; 4-жды 8 составляет 32. Вычитая 32, получим в остатке нуль.

3. Сносим 8; 8 в 8-ми содержится 1 раз, 1-жды 8 составляет 8. Вычитая 8, получаем в остатке нуль и в частном 541.

Как правильно делить числа в столбик: алгоритм деления

Для деления чисел столбиком следуйте по таким шагам:

• правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
• разлинейте место между делимым и делителем.
  Вам поможет схема ниже.

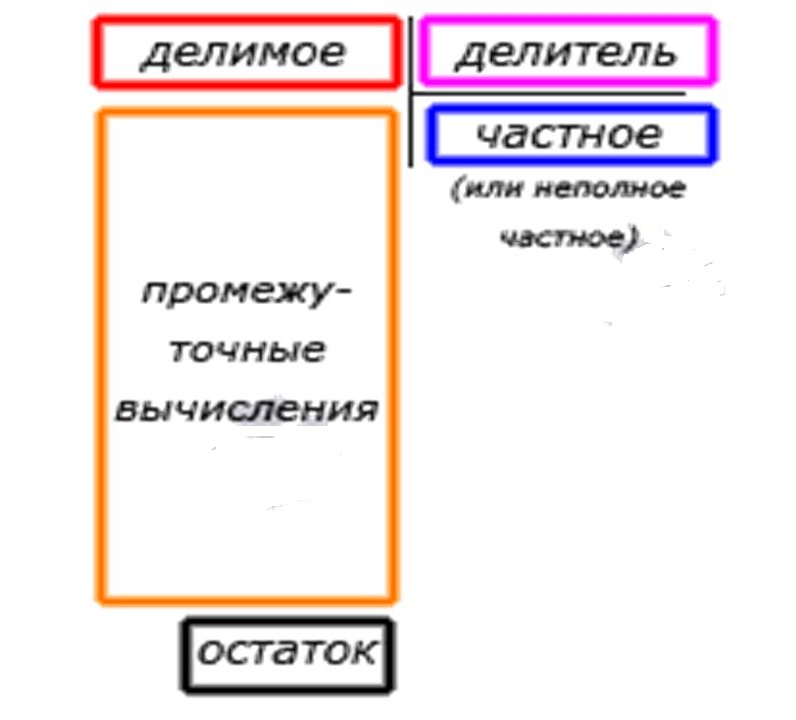
• планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
• первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
• перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
• завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
• допишите следующую цифру делимого к остатку и продолжайте решение,
• последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.

Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение

Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.

Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.

Схематически он выглядит так:

В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.

Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.

Схема деления трехзначного на двузначное числа такая:

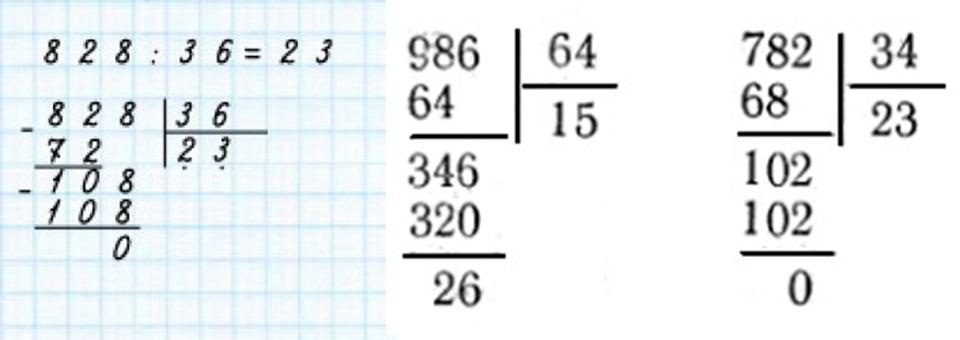
Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.

Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.

Схема деления трёхзначного на трёхзначное числа.

Как правильно подготовить ребенка к восприятию нового материала?

Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.

Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.

Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ