Примеры
Задача 1. Найдите количество всех двузначных чисел, делящихся на 3 без остатка.
Решение:
Чтобы определить количество 2-х значных натуральных чисел, делящихся на 3, нам сначала нужно вспомнить признак делимости на 3.
Мы можем начать с перечисления всех вариантов и проверки того, какие из них делятся на 3.
Вот они: 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99. Пересчитаем и увидим, что их всего 30. Но есть и более простой способ решения этой задачи — альтернативный.
В качестве альтернативы мы можем использовать более математический подход, чем простое подсчитывание. Мы знаем, что двузначные натуральные числа находятся в диапазоне от 10 до 99 и их всего 90. Мы можем найти количество тех из них, которые делятся на 3, путем деления 90 на количество возможных исходов для каждых трех.
Каждое третье, начиная с 12, будет делиться на 3: 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42…93, 96, 99. То есть, повторимся для лучшего понимания, из 90 каждое третье будет делиться на 3.
Тогда если мы разделим 90 на 3, мы получим 30 без остатка.
Ответ: 30
Задача 2. Определите количество двузначных чисел, делящихся на 5 без остатка.
Решение:
Число делится на 5, если оно оканчивается на 0 или 5. Следовательно, чтобы найти количество двузначных натуральных чисел, которые делятся на 5, нам нужно найти те из них, которые оканчиваются на 0 или 5.
Сначала мы рассмотрим оканчивающиеся на 0. Это числа от 10 до 99, которые кратны 10. Мы знаем, что между 10 и 99 есть 9 чисел кратных 10, то есть 10, 20, 30, 40, 50, 60, 70, 80 и 90.
Теперь мы рассмотрим те, что оканчиваются на 5. Мы знаем, что между 15 и 95 существует 9 чисел кратных 5, то есть 15, 25, 35, 45, 55, 65, 75, 85, 95.
Чтобы получить общее количество, складываем оканчивающиеся на 0 и оканчивающиеся на 5:
9 (оканчивающиеся на 0) + 9 (оканчивающиеся на 5) = 18
Следовательно, существует 18 двузначных натуральных чисел, делящихся на 5. Это числа: 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90.
Ответ: 18.
Задача 3. В ящике находятся шары, на них нанесены только двузначные числа. Маша вынимает шар, определите вероятность того, что число на шаре будет делиться на 5.
Ответ: Всего чисел, кратных пяти — восемнадцать (смотрите предыдущую задачу). Маша может достать любой шар. Благоприятных исходов 18. А всего исходов — 90.
Таким образом, рассчитываем вероятность, как отношение количества благоприятных исходов к общему количеству исходов.
P=18/90= 0,2.
Ответ: 0,2.
Задача 3. Сколько всего двузначных чисел, в записи которых есть цифра 1?
Решение: опираясь на список, можно просто выписать все его элементы, удовлетворяющие условию задачи:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19,
20, 21, 22, 23, 24, 25, 26, 27, 28, 29
30, 31, 32, 33, 34, 35, 36, 37, 38, 39
40, 41, 42, 43, 44, 45, 46, 47, 48, 49
50, 51, 52, 53, 54, 55, 56, 57, 58, 59
60, 61, 62, 63, 64, 65, 66, 67, 68, 69
70, 71, 72, 73, 74, 75, 76, 77, 78, 79
80, 81, 82, 83, 84, 85, 86, 87, 88, 89
90, 91, 92, 93, 94, 95, 96, 97, 98, 99.
Это будут: все элементы первого ряда 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 — здесь цифра 1 стоит в разряде десятков. И по одному элементу из каждого из следующих рядов: 21, 31, 41, 51, 61, 71, 81, 91. Итого: 18.
Ответ: 18.
Что узнали. Чему научились
Номер 1.
Вычисли с устным объяснением и проверкой.
Ответ:

1) Пишу десятки под десятками, а единицы под единицами.
Складываю единицы:
2 + 5 = 7
Пишу под единицами 7.
Складываю десятки:
3 + 4 = 7
Пишу под десятками 7.
Читаю ответ: сумма чисел 32 и 45 равна 77.
Пишу десятки под десятками, а единицы под единицами.
Вычитаю единицы:
8 − 3 = 5
Пишу под единицами 5.
Вычитаю десятки:
6 − 4 = 2
Читаю ответ: разность чисел 68 и 43 равна 25.
Пишу десятки под десятками, а единицы под единицами.
Складываю единицы:
4 + 3 = 7
Пишу под единицами 7.
Складываю десятки:
5 + 1 = 6
Пишу под десятками 6.
Читаю ответ: сумма чисел 54 и 13 равна 67.
Пишу десятки под десятками, а единицы под единицами.
Вычитаю единицы:
9 − 6 = 3
Пишу под единицами 3.
Вычитаю десятки:
7 − 5 = 2
Пишу под десятками 2.
Читаю ответ: разность чисел 79 и 56 равна 23.
2) Пишу десятки под десятками, а единицы под единицами.
Складываю единицы:
7 + 8 = 15
15 ед. − это 1 дес. и 5 ед. 5 ед записываю под единицами, а 1 дес. запоминаю.
Пишу под единицами 5
Складываю десятки:
5 + 3 = 8, да еще 1 десяток
8 + 1 = 9
Пишу под десятками 9.
Читаю ответ: сумма чисел 57 и 38 равна 95.
Пишу десятки под десятками, а единицы под единицами.
Складываю единицы:
3 + 7 = 10
10 ед. − это 1 дес. и 0 ед. 0 ед записываю под единицами, а 1 дес. запоминаю.
Пишу под единицами 0
Складываю десятки:
7 + 1 = 8, да еще 1 десяток
8 + 1 = 9
Пишу под десятками 9.
Читаю ответ: сумма чисел 73 и 17 равна 90.
Пишу десятки под десятками, а единицы под единицами.
Складываю единицы:
4 + 6 = 10
10 ед. − это 1 дес. и 0 ед. 0 ед записываю под единицами, а 1 дес. запоминаю.
Пишу под единицами 0
Складываю десятки:
6 + 2 = 8, да еще 1 десяток
8 + 1 = 9
Пишу под десятками 9.
Читаю ответ: сумма чисел 64 и 26 равна 90.
Пишу десятки под десятками, а единицы под единицами.
Складываю единицы:
7 + 3 = 10
10 ед. − это 1 дес. и 0 ед. 0 ед записываю под единицами, а 1 дес. запоминаю.
Пишу под единицами 0
Складываю десятки:
8 + 1 = 9, да еще 1 десяток
9 + 1 = 10. 10 дес. − 1 сот. и 0 дес. записываю под сотнями 1, а под десятками 0.
Читаю ответ: сумма чисел 87 и 13 равна 100.
Пишу десятки под десятками, а единицы под единицами.
Складываю единицы:
2 + 3 = 5
Пишу под единицами 5.
Складываю десятки:
5 + 4 = 9,
Пишу под десятками 9.
Читаю ответ: сумма чисел 42 и 53 равна 95.
3) Пишу десятки под десятками, а единицы под единицами.
Вычитаю единицы: из 0 нельзя вычесть 8.
Беру 1 дес. из 4 дес. (чтобы не забыть, ставлю точку над цифрой 4).
1 дес. = 10 ед. 10 − 8 = 2
Пишу под единицами 2.
Вычитаю десятки:
Было 4 дес., но 1 дес. взяли при вычитании единиц.
Осталось 3 дес.
3 − 1 = 2
Пишу 2 под десятками.
Читаю ответ: разность чисел 40 и 18 равна 22.
Пишу десятки под десятками, а единицы под единицами.
Вычитаю единицы: из 0 нельзя вычесть 4.
Беру 1 дес. из 5 дес. (чтобы не забыть, ставлю точку над цифрой 5).
1 дес. = 10 ед. 10 − 4 = 6
Пишу под единицами 6.
Вычитаю десятки:
Было 5 дес., но 1 дес. взяли при вычитании единиц.
Осталось 4 дес.
4 − 2 = 2
Пишу 2 под десятками.
Читаю ответ: разность чисел 50 и 24 равна 26.
Пишу десятки под десятками, а единицы под единицами.
Вычитаю единицы: из 2 нельзя вычесть 8.
Беру 1 дес. из 4 дес. (чтобы не забыть, ставлю точку над цифрой 4).
1 дес. = 10 ед. 12 − 8 = 4
Пишу под единицами 4.
Вычитаю десятки:
Было 4 дес., но 1 дес. взяли при вычитании единиц.
Осталось 3 дес.
3 − 1 = 2
Пишу 2 под десятками.
Читаю ответ: разность чисел 42 и 18 равна 24.
Пишу десятки под десятками, а единицы под единицами.
Вычитаю единицы: из 6 нельзя вычесть 7.
Беру 1 дес. из 5 дес. (чтобы не забыть, ставлю точку над цифрой 5).
1 дес. = 10 ед. 16 − 7 = 9
Пишу под единицами 9.
Вычитаю десятки:
Было 5 дес., но 1 дес. взяли при вычитании единиц.
Осталось 4 дес.
4 − 2 = 2
Пишу 2 под десятками.
Читаю ответ: разность чисел 56 и 27 равна 29.
Пишу десятки под десятками, а единицы под единицами.
Вычитаю единицы:
6 − 3 = 3
Пишу под единицами 3.
Вычитаю десятки:
9 − 4 = 5
Пишу 5 под десятками.
Читаю ответ: разность чисел 96 и 43 равна 22.
Номер 2.
Ответ:

Номер 3.
Найди значения выражений a + 8 и b − 6 при a = 14, a = 8, a = 6, a = 0 и b = 13, b = 18, b = 44, b = 50.
Ответ:
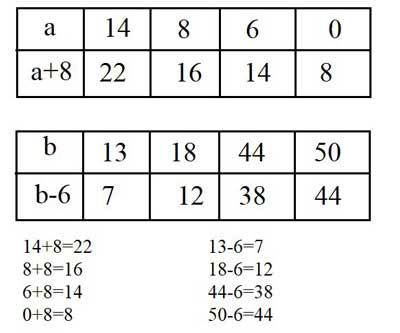
Номер 4.
Выпиши уравнения, решением которых является число 7.
Ответ:
Ответ: 15 − х = 8, х + 40 = 47, 14 − х = 7, 17 − х = 10, 16 − х = 9, 27 − х = 20.
Проверим:
15 − х = 8
х = 15 − 8
х = 7
х + 40 = 47
х = 47 − 40
х = 7
14 − х = 7
х = 14 − 7
х = 7
17 − х = 10
х = 17 − 10
х = 7
16 − х = 9
х = 16 − 9
х = 7
27 − х = 20
х = 27 − 20
х = 7
Номер 5.
Используя числа 21, 14, 8 и 7, составь по 2 верных равенства и неравенства.
Ответ:
14 + 7 = 21 21 − 7 = 14
21 + 8 > 14 + 7 14 − 8 < 7
Номер 6.
Ответ:
80 − (24 − 6) = 80 – 18 = 62
90 − (36 − ![]() = 90 – 28 = 62
= 90 – 28 = 62
48 + (13 + 7) = 48 + 20 = 68
34 + (18 + 2) = 34 + 20 = 54
89 − (64 − 4) = 89 – 60 = 29
75 − (37 − 7) = 75 – 30 = 45
Номер 7.
Ответ:
8 + 7 − 6 = 15 – 6 = 9
4 + 9 − 7 = 13 – 7 = 6
12 − 7 + 9 = 5 + 9 = 14
16 − 8 + 9 = 8 + 9 = 17
6 + 6 − 8 = 12 – 8 = 4
7 + 7 − 5 = 14 – 5 = 9
Номер 8.
Ответ:
8 + 4 + 4 = 8 + 8 = 16
7 + 9 + 4 = 16 + 4 = 20
15 − 7 − 8 = 8 − 8 = 0
17 − 7 − 10 = 10 − 10 = 0
9 + 0 + 11 = 9 + 11 = 20
9 − 9 + 15 = 0 + 15 = 15
Задание на полях страницы
Ребусы:
Ответ:
Немного истории математики
Понятие двузначных чисел, то есть состоящих из двух цифр, берет свое начало в развитии ранних систем счета. В ранних цивилизациях счет в основном производился с помощью пальцев, и это был первый способ счета. Люди считали на пальцах рук и ног, чтобы представлять сколько у них предметов, продуктов, добычи.
По мере того как общества становились более сложными и возникала потребность в более сложных способах счета, люди начали использовать другие объекты для представления количества. Они начали использовать камешки, палочки или другие мелкие предметы, а затем помещали их в группы, чтобы представить большие числа. Такое представление называется «система подсчета».
По мере развития системы подсчета люди начали использовать символы, и именно здесь мы видим начало происхождения системы счисления. В первых системах счисления использовались простые метки или символы, например, линия для обозначения единицы, две линии для обозначения двух и так далее.
Со временем эти символы стали более сложными и изощренными, и, в конце концов, была разработана концепция позиционной записи. Разрядность — это концепция представления чисел с помощью цифр, где каждая цифра представляет разную степень числа 10. Например, в записи 42 — 4 представляет четыре десятка, а 2 — две единицы.
Эта система позволяла представлять гораздо большие числа с использованием меньшего количества символов, а также делала арифметические операции, такие как сложение и вычитание, намного более эффективными. Это та система, которую мы используем до сих пор.
Похожая статья — сколько всего трехзначных чисел.






























