Умножение суммы на число
Задание. Посчитайте и запишите решение на вопрос: сколько квадратов в прямоугольнике?
Вариант 1. Рассуждайте так: в ряду шесть синих квадратов плюс три красных квадрата. Рядов 4. Значит, запишите решение:
Сумма в скобках равна девяти. 9 ∙ 4 = 36. Это табличное умножение.
Вариант 2. Количество квадратов подсчитайте другим способом. Узнайте, сколько синих, потом, сколько красных, полученные результаты сложите.
Таким способом удобно умножать большие величины.
Любое двузначное число легко записать как сумму разрядных слагаемых: круглых десятков и единиц.
Умножайте сначала десятки, потом единицы, произведения складывайте.
Как это сделать, рассмотрите на примере.
Сумму десяти и пяти умножим на шесть.
Это распределительное свойство умножения суммы на число.
Правило умножения суммы на число запишите буквенным выражением.
За внимание награждаю вас оранжевой лентой. Идите по маршруту дальше
Идите по маршруту дальше.
Умножение двузначного числа на однозначное
Сейчас будем решать вот такие примеры:
Они такие легкие, что мы разделаемся с ними на раз, два, три.
Устное умножение чисел двузначного на однозначное
Считать устно — это просто замечательно, я сам стараюсь обходиться без калькулятора. Но для того, чтобы это делать, нужно знать приемы устного счета. Это чудесная разминка для мозга.
Мы разберемся с примерами, когда двузначное число умножается на однозначное. Вы научились записывать сумму разрядных слагаемых, поэтому воспользуемся этим умением.
Давайте тренироваться:
Пример сложнее.
89 умножить на семь.
Ну как, простые примеры? По способу решения — да. А вот, если не знаете таблицу умножения, то не такие уж простые.
Умножение столбиком двузначного числа на однозначное
Это письменный прием вычислений. Такие примеры мы привыкли называть примеры в столбик или примеры столбиком. Давайте научимся правильно записывать такое решение.
Пусть надо 58 умножить на семь.
А теперь начните решать. Последовательно умножьте слева направо все цифры первого множителя на 7, пока они не закончатся. Умножаем 8 на 7, это 56. Что нам с ним делать? Смотрите, то, что единицы, мы так и записываем.
Процесс умножения закончен. Читаем ответ — четыреста шесть.
Давайте посмотрим другой пример.
Запишите столбиком.
Проверьте, как записали.
Выполните вычисления. 5 ∙ 9 = 45. Пять записываем под девяткой. Четыре в уме.
4 ∙ 9 = 36. Да 4 в уме. 36 + 4 = 40. Записываем значение произведения. Читаем ответ — 405.
Проверьте свою запись.
Будем учиться решать уравнения, в котором неизвестным является уменьшаемое.
Номер 1
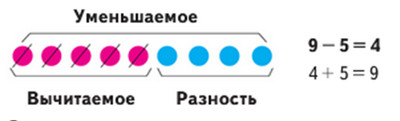
Объясни, что получится, если из суммы двух слагаемых вычесть одно из них.
Закончи вывод.
Если к разности прибавить вычитаемое, получится … .
Зная это, можно решать уравнения, в которых неизвестным является уменьшаемое
Решение:
Если к разности прибавить вычитаемое, получится уменьшаемое.
Номер 2
Объясни решение уравнения и проверку.
х — 20 = 31
х = 31 + 20
х = 51
Проверка:
51 — 20 = 31
31 = 31
Решение:
Объясняю решение уравнения.
х – уменьшаемое, 20 – вычитаемое, 31 – разность. Неизвестно уменьшаемое. Чтобы найти уменьшаемое надо к разности прибавить вычитаемое: х = 31 + 20, х = 51.
Проверка. В уравнение х – 20 = 31 вставляем 51 вместо х: 51 – 20 = 31. Вычисляем, сравниваем значение выражений слева и справа: 32 = 32. Уравнение решено правильно.
Пояснение:
Чтобы найти вычитаемое, надо к разности прибавить уменьшаемое.
Номер 3
Реши уравнение с объяснением.
b – 8 = 54, х – 36 = 40, k + 14 = 20
Решение:
b – 8 = 54
b = 54 + 8
b = 62
Проверка:
62 – 8 = 54
54 = 54
Объясняю решение уравнения.
Неизвестно уменьшаемое. Чтобы найти уменьшаемое, надо к разности 54 прибавить вычитаемое 8.
Делаю проверку.
В уравнение вместо неизвестного уменьшаемого вставляю 62.
Вычисляю. Левая и правая части выражения равны 54 – уравнение решено правильно.
х – 36 = 40
х = 40 + 36
b = 76
Проверка:
76 – 36 = 40
40 = 40
Объяснение решения такое же.
k + 14 = 20
k = 20 – 14
b = 6
Проверка:
6 + 14 = 20
20 + 20
Объясняю решение уравнения.
Неизвестно первое слагаемое. Чтобы найти первое слагаемое, надо из суммы 20 вычесть второе слагаемое 14.
Делаю проверку.
Вставляю вместо неизвестного слагаемого 6.
Вычисляю. Левая и правая части выражения равны 20 – уравнение решено правильно.
Пояснение:
При решении уравнений надо повторить правила, как найти неизвестное уменьшаемое, слагаемое. Проверку делать обязательно.
Номер 4
Запиши столбиком решение и проверку.
49 – 35; 32 – 17
68 – 18; 80 – 65
Решение:
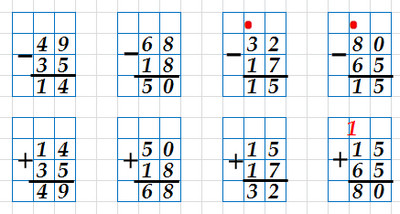
Пояснение:
Вычитание проверяем сложением – к разности прибавить вычитаемое получим уменьшаемое.
Номер 5
Найди значения суммы и разности чисел b и 10 при b = 36, b = 57, b = 63, b = 10.
Решение:
36 + 10 = 46
36 – 10 = 26
57 + 10 = 67
57 – 10 = 47
63 + 10 = 73
63 – 10 = 53
10 + 10 = 20
10 – 10 = 0
Пояснение:
Чтобы найти значение буквенного выражения, надо в выражение вставить значение переменой.
Номер 6
7 + 7 о 7 + 7 +7
2 см о 1 см 8 мм
9 + 9 +9 о 9 +9
3см 6 мм о 4 см
Решение:

Пояснение:
Чтобы сравнить значение выражений, надо произвести действия с ними, результаты сравнить. Именованные числа надо выразить в меньших единицах.
Можно сравнить не производя действий, не преобразовывая: 2 семёрки меньше, чем 3
семёрки, 2 см меньше 1 см (при устном объяснении).
Номер 7
На клумбе расцвели 15 красных астр, розовых на 3 меньше, а белых астр столько, сколько красных и розовых вместе. Сколько белых астр?
Решение:

1) 15 – 3 = 12 (астр) – розовых.
2) 15 + 12 = 27 (астр) – белых.
Ответ: 27 белых астр.
Пояснение:
Чтобы узнать, сколько белых астр расцвело, нужно знать, сколько расцвело розовых и красных астр. Сколько красных – известно, сколько розовых – надо узнать.
Номер 8
![]()
Решение:
48 + 49 + 2 = 48 + 2 + 49 = 50 + 49 = 99
56 + 27 + 3 = 27 + 3 + 56 = 30 + 56 = 86
69 − (26 + 24) = 69 − 50 = 19
69 − 26 + 24 = 43 + 24 = 67
30 − 22 = 8
80 − 4 = 76
44 − 30 = 14
84 − 5 = 79
Пояснение:
Применяем переместительный и сочетательный законы сложения, чтобы при выполнении действий с числами получалось круглое число. При сложении и вычитании чисел действия сначала производят с единицами, а затем с десятками.
Номер 9
Какой из двух отрезков длиннее? Определи на глаз, а затем проверь измерением.
Решение:
На глаз отрезки одинаковые.
Измеряю.
Длина синего отрезка – 4 см.
Длина красного отрезка – 4 см.
Пояснение:
Необходимо измерить отрезки, чтобы сравнить их длины.
Задание под чертой
Найди среди записей уравнение и реши его.
Решение:
Пояснение:
Уравнение – это равенство с переменной. Решить его – найти значение переменной, при котором равенство будет верным.
Задание на полях
Решение:
Пояснение:
Чтобы заполнить рамки, нужно сложить числа, размещённые по сторонам рамки, а затем сумму вычесть из числа, находящегося в середине рамки.
Стр 7
Стр 9
Вернуться к содержанию: Математика 3 класс учебник Моро
Часть 2:
Страница 4
1
2
3
4
5
6
7
?
Страница 5
1
2
3
4
5
6
7
?
Страница 6
1
2
3
?
Страница 7
1
2
3
4
5
6
7
8
?
Страница 8
1
2
3
4
5
6
7
?
Страница 9
1
2
3
4
5
6
7
8
9
?
Страница 10
1
2
3
4
5
6
7
8
9
?
Страница 11
1
2
3
4
?
Страница 12. Странички для любознательных
1
2
3
4
Страница 13
1
2
3
4
5
6
?
Страница 14
1
2
3
4
5
6
?
Страница 15
1
2
3
4
5
6
7
?
Страница 16
1
2
3
4
5
6
?
Страница 17
1
2
3
4
5
6
?
Страница 18
1
2
3
4
5
6
7
?
Страница 19
1
2
3
4
5
6
7
?
Страница 20
1
2
3
4
5
6
7
8
?
Страница 21
1
2
3
4
5
6
7
8
9
10
Страница 22-23. Странички для любознательных
1
2
3
Страница 24-25. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
Страница 26
1
2
3
4
5
?
Страница 27
1
2
3
4
5
?
Страница 28
1
2
3
4
5
6
7
?
Страница 29
1
2
3
4
5
6
?
Страница 30
1
2
3
4
5
6
?
Страница 31
1
2
3
4
5
6
7
8
Страница 32
1
2
3
4
5
6
7
?
Страница 33-35. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Страница 38-39. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
10
11
Вариант 2
1
2
3
4
5
6
7
8
9
10
11
Страница 40. Странички для любознательных
1
2
Страница 42
1
2
3
4
5
6
7
8
?
Страница 43
1
2
3
4
5
6
7
?
Страница 44
1
2
3
4
Страница 45
5
6
7
8
9
10
11
12
?
Страница 46
1
2
3
4
5
6
7
8
9
10
?
Страница 47
1
2
3
4
5
6
7
?
Страница 48
1
2
3
4
5
6
?
Страница 49
1
2
3
4
5
6
7
8
?
Страница 50
1
2
3
4
5
6
?
Страница 51
1
2
3
4
5
6
7
8
9
Страница 52-53. Странички для любознательных
1
2
3
4
5
6
7
8
Страница 54
1
2
3
4
5
?
Страница 55. Задачи — Расчеты
1
2
3
4
Страница 56-57. Странички для любознательных
1
2
3
4
Страница 58-61. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Страница 62-63. Проверим себя и оценим свои достиженияВариант 1
1
2
3
4
5
6
7
8
9
Вариант 1
1
2
3
4
5
6
7
8
9
Страница 64. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
Страница 66
1
2
3
4
5
6
7
?
Страница 67
1
2
3
4
5
6
7
8
?
Страница 68
1
2
3
4
5
?
Страница 69
1
2
3
4
5
6
7
?
Страница 70
1
2
3
4
5
6
7
8
9
?
Страница 71
1
2
3
4
5
6
?
Страница 72
1
2
3
4
5
6
7
?
Страница 73
1
2
3
4
Страница 74
1
2
3
4
5
6
?
Страница 75. Странички для любознательных
1
2
3
4
5
Страница 76-79. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Страница 80. Странички для любознательных
1
2
3
4
5
6
7
8
9
10
11
Страница 82
1
2
3
4
5
6
7
?
Страница 83
1
2
3
4
5
6
7
?
Страница 84
1
2
3
4
5
6
7
8
?
Страница 85
1
2
3
4
5
?
Страница 86
1
2
3
4
?
Страница 87. Странички для любознательных
1
2
3
Страница 88
1
2
3
4
5
?
Страница 89
1
2
3
4
5
6
?
Страница 90
1
2
3
4
5
6
7
8
?
Страница 91
1
2
3
4
5
6
?
Страница 92
1
2
3
4
5
6
7
?
Страница 93
1
2
3
Страница 94
4
5
6
?
Страница 95
1
2
3
4
5
6
7
?
Страница 96
1
2
3
4
5
6
7
8
Страница 98
1
2
3
4
5
6
?
Страница 99-102. Что узнали. Чему научились
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Что узнали, чему научились в 3 классе?Страница 103. Нумерация
1
2
3
4
5
6
7
8
Страница 103-104. Сложение и вычитание
1
2
3
4
5
6
7
8
Страница 105-106. Умножение и деление
1
2
3
4
5
6
7
8
Страница 107. Правила о порядке выполнения действий
1
Страница 107-108. Задачи
1
2
3
4
5
6
7
8
9
10
11
Страница 109. Геометрические фигуры и величины
1
2
3
4
5
Тексты для итоговой контрольной работыСтраница 110. Задания базового уровня
1
2
3
4
5
6
7
Страница 111. Задания повышенного уровня
1
2
3
4
5
6
7
Деление двузначного числа на однозначное
Ребята, вы меня узнали? Люблю наряжаться на маскарад. Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.
Такие задания называют примерами с «усиками». Да, да, но усики носят не люди, кто делит, а сами примеры. Рисовать их нужно простым карандашом, а когда научитесь быстро считать, то просто представляйте в голове.
Устное деление двузначного на однозначное
Задание 1.
Пусть надо решить, сколько будет
К «усикам» запишем такие два слагаемых, которые делятся на 8, а в сумме дают 96.
Самое главное — это не ошибиться в подборе первого «усика». Надо запомнить, что он всегда больше, чем второй. Ищем его, умножая 8 на 10. Если не подойдет, то будем умножать на 20, на 30. Главное, чтобы было круглое число.
Все понятно? Будем тренироваться.
Задание 2.
Задание 3.
Попробуем разделить 90 на два. «Первый усик» явно не 20, тогда второй будет 70. Знаем, что «второй усик» не может быть больше первого.
Вижу, что не 60, потому что 30 разделить на два — это не табличный случай.
Следовательно, 2 ∙ 40 = 80. Значит «первый усик» предположительно 80. «Второй усик» тогда найдем вычитанием: 90 – 80 = 10. Десять разделить на два, это таблица.
Как думаете, вы справитесь с делением? Когда встречаете случаи, где двузначное число делится на однозначное, и примеры не относятся к таблице умножения, то решайте подбором «усиков». Разбивайте делимое на подходящие слагаемые. Их можно записать суммой в скобочках, а при делении использовать правило деления суммы на число.
Решите задачу.
Таня выполнила 96 примеров, а Коля в 4 раза меньше. Сколько примеров решил Коля?
Чтобы ответить на вопрос задачи, надо выполнить действие деления.
96 : 4 =
«Усиками» будут 80 и 16, получается сумма 80 + 16. Значит, каждое из этих слагаемых разделите на 4, а частные сложите.
Ответ: 24
Деление столбиком двузначное на однозначное
Письменное деление уголком просто невозможно усвоить без блестящего знания таблицы умножения. Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.
Задание 1.
Пусть надо 84 разделить на три. Посмотрите на запись. Такой значок означает деление уголком. Уголок имеет наверху делитель, на который делим. Под чертой — результат, который ищем. Он называется частным.
Нам надо узнать, чему равно частное. Но прежде определим, сколько цифр будет в результате. Это очень важный шаг, поэтому упускать его нельзя. Как мы будем это делать? Посмотрите на первую цифру. Это восьмерка. Восемь больше трех. Значит, она может дать нам полноценную цифру в частном. Ставим точку. После восьмерки еще одна цифра, это значит, что частное — двузначное число. Под чертой в уголке карандашом поставьте вторую точку.
Первое неполное делимое — восьмерка. Начинаем ее делить на три, ищем табличный случай. Легче всего уменьшать 8 на единицу.
8 – 1 = 7. В таблице нет деления семи на три.
Уменьшаем еще на 1.
7 – 1 = 6. Шесть делится на три, получается — по два. Записываем 2 в частное под чертой.
Теперь мы должны понять, сколько не разделили. Ведь разделили всего шесть.
А надо было разделить восемь.
Два осталось неразделенным. Это остаток. Он должен быть меньше делителя.
Давайте проверим: два меньше трех.
Да, действительно. Мы сделали все правильно. Этот шаг очень важен. Не забывайте сравнивать остаток с делителем.
После этого сносим следующую цифру с тем, чтобы получить новое неполное делимое
Обратите внимание: нужно писать каждую цифру в своей клетке. Получается неполное делимое 24
Ответ: 28.
Задание 2.
Решите пример столбиком 96 : 4 =
Проверьте:
Ура! Наш математический маршрут пройден. Знания-сокровища из цветных лент превратились в волшебную радугу. Что же у нас вышло, что мы унесем в нашем сундуке. Закончите предложения:
Умножение и деление круглых чисел
Обратите внимание: круглым называется число, которое оканчивается нулем — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Круглые числа похожи на десятки
Разряд единиц круглых десятков равняется нулю.
Прочитайте таблицу круглых чисел:
Умножение и деление круглого двухзначного числа на однозначное выполняется по определенным правилам. Познакомьтесь с этими правилами.
Деление круглых чисел
Рассмотрим пример внетабличного деления:
В примерах деления круглого числа делим количество десятков и дописываем в ответе нуль.
Делим на 10 — убираем в ответе нуль.
В частном не пишем нули, если делимое, делитель — круглые числа.
Умножение круглых чисел
А знаете ли вы, что за тысячелетия развития математики было придумано много вариантов умножения. Считалось, что для овладения искусством вычисление нужен талант. Итальянский математик 15 века Лука Пачоли приводит 8 способов. Познакомимся с некоторыми из них.
Рассмотрите прием внетабличного умножения.
Двадцать умножить на три равно шестидесяти.
Воспользуемся правилом перестановки множителей, получим пример, который умеем решать.
Прочитайте правило внимательно.
При умножении круглого числа на однозначное, надо умножить десятки на второй множитель, в ответ справа добавить нуль.
Увеличить в десять раз — это значит написать в значение произведения первый множитель и добавить к нему 0 справа.
Произведение семи и десяти равно семидесяти.
Воспользуйтесь правилами математики внетабличного умножения и деления для решения примеров:
Проверьте:
Ошибок нет, молодцы. Ваша первая награда — красная ленточка.
Впереди ждут новые открытия, не отставайте, думайте, решайте.
Деление суммы на число
Прочитайте рассказ «Из истории символов».
Люди сначала умножали, делить научились позднее. В десятом веке ученый Герберт в математических трудах упомянул сложные правила «железного деления». Старинная итальянская поговорка гласила: «Трудное дело — деление»
Оно и в самом деле было трудно, если принять во внимание утомительные методы, какими выполнялось тогда это действие.
В середине 18 века в странах Европы начали делить привычным для нас простым способом, который изобрели арабы. Он получил название «золотое деление».
Для записи действия применяются разные знаки:
В 17 веке в Англии и США чаще всего использовался обелюс. Символ в виде двух точек придумал немецкий математик Г. Лейбниц в 1684 году. На письме он очень похож на двоеточие.
Познакомимся со способом деления. Выполните задание.
Какие числа нужно вставить в «окошки», чтобы получились верные равенства?
Решение.
Рассуждаем: первое слагаемое — круглое число. В окошко нужно подставить слагаемое, которое делится на три без остатка.
Подсказка: вспомните результаты табличного умножения на 3. Например, 27.
Деление суммы чисел 30 и 27 на данное число 3 вычисляется так: каждое слагаемое делится на три и результаты складываются.
Запишите подробное решение:
Сформулируйте правило деления суммы на число:






























