Несколько слов в защиту учителей …
Несправедливо и неправильно всю ответственность за такой стиль обучения сваливать исключительно на школьных учителей. Действует система.
Некоторые учителя понимают абсурдность происходящего, но что делать? Закон об образовании, ФГОСы, методики, технологические карты уроков … Все должно делаться «в соответствии и на основании» и все должно быть задокументировано. Шаг в сторону — встал в очередь на увольнение. Не будем ханжами: зарплата московских учителей ну очень неплохая … Уволят — куда идти?..
Поэтому сайт этот не об образовании. Он об индивидуальном образовании, единственно возможном способе выбраться из толпы поколения Z …
Метод Гаусса в 5 классе школы
Оговорюсь сразу: метод Гаусса имеет гораздо более широкое применение, например, при решении систем линейных уравнений. То, о чем мы будем говорить, проходят в 5 классе. Это начала, уяснив которые, гораздо легче разобраться в более «продвинутых вариантах». В этой статье мы говорим о методе (способе) Гаусса при нахождении суммы ряда
Вот пример, который принес из школы мой младший сын, посещающий 5 класс московской гимназии.
Школьная демонстрация метода Гаусса
… Учитель математики с использованием интерактивной доски (современные методы обучения ) показал детям презентацию истории «создания метода» маленьким Гауссом.
… Школьный учитель выпорол маленького Карла (устаревший метод, нынче в школах не применяется) за то, что тот,
вместо того, чтобы последовательно складывая числа от 1 до 100 найти их сумму заметил, что пары чисел, равно отстоящие от краев арифметической прогрессии, в сумме дают одно и то же число. например, 100 и 1, 99 и 2. Посчитав количество таких пар, маленький Гаусс почти моментально решил предложенную учителем задачу. За что и был подвергнут экзекуции на глазах изумленной публики. Чтобы остальным думать было неповадно.
Что сделал маленький Гаусс, развивший чувство числа? Заметил некоторую особенность числового ряда с постоянным шагом (арифметической прогрессии). И именно это сделало его впоследствии великим ученым, умеющим замечать, обладающим чувством, инстинктом понимания.
… Этим и ценна математика, развивающая способность видеть общее в частном — абстрактное мышление
Поэтому большинство родителей и работодателей инстинктивно считают математику важной дисциплиной …. Однако, последователи тех, кто порол розгами будущих гениев, превратили Метод в нечто противоположное
Как 35 лет назад говорил мой научный руководитель: «Занаучили вопрос». Или как сказал вчера о методе Гаусса мой младший сын: «Может не стоит из этого большую науку делать-то, а?»
Однако, последователи тех, кто порол розгами будущих гениев, превратили Метод в нечто противоположное. Как 35 лет назад говорил мой научный руководитель: «Занаучили вопрос». Или как сказал вчера о методе Гаусса мой младший сын: «Может не стоит из этого большую науку делать-то, а?»
Последствия творчества «ученых» видны по уровню нынешней школьной математики, уровню ее преподавания и понимания «Царицы наук» большинством.
Однако, продолжим …
Главное преступление учителя математики
Вряд ли после того случая Карл Гаусс испытал высокое чувство уважения по отношению к школьному учителю математики. Но если бы он знал, как последователи того учителя извратят самую суть метода … он взревел бы от негодования и через Всемирную организацию интеллектуальной собственности ВОИС добился запрета на использование своего честного имени в школьных учебниках!..
В чем главная ошибка школьного подхода? Или, как я выразился — преступление школьных учителей математики против детей?
Алгоритм непонимания
Что делают школьные методисты, абсолютное большинство которых думать не умеет ни фига?
Создают методики и алгоритмы (см. статью об этом). Это защитная реакция, предохраняющая учителей от критики («Все делается согласно …»), а детей — от понимания. И таким образом — от желания критиковать учителей! (Вторая производная чиновничьей «мудрости», научный подход к проблеме ). Человек не улавливая смысл скорее будет пенять на собственное непонимание, а не на тупость школьной системы.
Что и происходит: родители пеняют на детей, а учителя … то же на детей, «не понимающих математику!..
Смекаете?
Что сделал маленький Карл?
Абсолютно нешаблонно подошел к шаблонной задаче. Это квинтэссенция Его подхода. Это главное, чему следует учить в школе: думать не учебниками, а головой. Конечно, есть и инструментальная составляющая, которую вполне можно использовать … в поисках более простых и эффективных методов счета.
Метод Гаусса по-Виленкину
В школе учат, что метод Гаусса состоит в том, чтобы
попарно находить суммы чисел, равноотстоящих от краев числового ряда, непременно начиная с краев!
находить число таких пар и т.д.
Но:
что, если число элементов ряда окажется нечетным, как в задаче, которую задали сыну?..
«Подвох» состоит в том, что в этом случае следует обнаружить «лишнее» число ряда и прибавить его к сумме пар. В нашем примере это число 260.
Как обнаружить? Переписывая все пары чисел в тетрадь! (Именно почему учительница заставила детей делать эту тупую работу, пытаясь научить «творчеству» методом Гаусса … И именно поэтому такой «метод» практически неприменим к большим рядам данных, И именно поэтому он не является методом Гаусса).
Немного творчества в школьной рутине …
Сын же поступил иначе.
Сначала он отметил, что умножать легче число 500, а не 520
(20 + 500, 40 + 480 …).
Потом он прикинул: количество шагов оказалось нечетным: 500 / 20 = 25.
Тогда он в начало ряда добавил НОЛЬ (хотя можно было и отбросить последний член ряда, что также обеспечило бы четность) и сложил числа, дающие в сумме 500
0+500, 20+480, 40+460 …
26 шагов это 13 пар «пятисоток»: 13 х 500 = 6500..
Если мы отбросили последний член ряда, то пар будет 12, но к результату вычислений следует не забыть прибавить «отброшенную» пятисотку. Тогда: (12 х 500) + 500 = 6500 !
Несложно, правда?
А практически делается еще легче, что и позволяет выкроить 2-3 минуты на ДЗ по русскому, пока остальные «считают». К тому же сохраняет количество шагов методики: 5, что не позволяет критиковать подход за антинаучность.
Явно этот подход проще, быстрее и универсальнее, в стиле Метода. Но … учительница не то, что не похвалила, но и заставила переписать «правильным образом» (см. скриншот). То есть предприняла отчаянную попытку задушить творческий импульс и способность понимать математику на корню! Видимо, чтобы потом наняться репетитором … Не на того напала …
Все, что я так долго и нудно описал можно объяснить нормальному ребенку максимум за полчаса. Вместе с примерами.
Причем так, что он это никогда не забудет.
И это будет шаг к пониманию … не только математики.
Признайтесь: сколько раз в жизни вы складывали методом Гаусса? И я ни разу!
Но инстинкт понимания, который развивается (или гасится) в процессе изучения математических методов в школе … О!.. Это поистине незаменимая вещь!
Особенно в век всеобщей цифровизации, в который мы незаметно вошли под чутким руководством Партии и Правительства.
Методы объяснения метода Гаусса в 5 классе школы
Учитель математики московской гимназии, объясняя метод Гаусса по-Виленкину, усложнил задание.
Что, если разность (шаг) арифметической прогрессии будет не единица, а другое число? Например, 20.
Задача, которую он дал пятиклассникам:
посчитать сумму ряда чисел:
20+40+60+80+ … +460+480+500
Прежде, чем познакомиться с гимназическим методом, заглянем в Сеть: как это делают школьные учителя — репетиторы по математике?..
Метод Гаусса: объяснение №1
Известный репетитор на своем канале YOUTUBE приводит следующие рассуждения:
«запишем числа от 1 до 100 следующим образом:
сначала ряд чисел от 1 до 50, а строго под ним другой ряд чисел от 50 до 100, но в обратной последовательности»
1, 2, 3, … 48, 49, 50
100, 99, 98 … 53, 52, 51
«Обратите внимание: сумма каждой пары чисел из верхнего и нижнего рядов одинакова и равняется 101 ! Посчитаем количество пар, оно составляет 50 и умножим сумму одной пары на количество пар! Вуаля: Ответ готов!». «Если вы не смогли понять — не расстраивайтесь!», — три раза в процессе объяснения повторил учитель
«Этот метод вы будете проходить в 9 классе!»
«Если вы не смогли понять — не расстраивайтесь!», — три раза в процессе объяснения повторил учитель. «Этот метод вы будете проходить в 9 классе!»
Метод Гаусса: объяснение №2
Другой репетитор, менее известный (судя по числу просмотров) использует более научный подход, предлагая алгоритм решения из 5 пунктов, которые необходимо выполнить последовательно.
Для непосвященных: 5 это одно из чисел Фибоначчи, традиционно считающееся магическим. Метод из 5 шагов всегда более научен, чем метод, например, из 6 шагов. … И это вряд ли случайность, скорее всего, Автор — скрытый приверженец теории Фибоначчи
Дана арифметическая прогрессия: 4, 10, 16 … 244, 250, 256.
Алгоритм нахождения суммы чисел ряда методом Гаусса:
Шаг 1: переписать заданную последовательность чисел наоборот, точно под первой.
4, 10, 16 … 244, 250, 256
256, 250, 244 … 16, 10, 4
Шаг 2: посчитать суммы пар чисел, расположенных в вертикальных рядах: 260.
Шаг 3: посчитать, сколько таких пар в числовом ряду. Для этого вычесть из максимального числа числового ряда минимальное и разделить на величину шага: (256 — 4) / 6 = 42.
При этом нужно помнить о правиле «Плюс один»: к полученному частному необходимо прибавить единицу: иначе мы получим результат, меньший на единицу, чем истинное число пар: 42 + 1 = 43.
Шаг 4: умножить сумму одной пары чисел на количество пар: 260 х 43 = 11 180
Шаг5: поскольку мы посчитали сумму пар чисел, то полученную сумму следует разделить на два: 11 180 / 2 = 5590.
Это и есть искомая сумма арифметической прогрессии от 4 до 256 с разницей 6 !
Метод Гаусса: объяснение в 5 классе московской гимназии
А вот как требовалось решить задачу нахождения суммы ряда:
20+40+60+ … +460+480+500
в 5 классе московской гимназии, учебник Виленкина (со слов моего сына).
… Показав презентацию, учительница математики показала пару примеров по методу Гаусса и дала классу задачу по нахождению суммы чисел ряда с шагом 20.
При этом требовалось следующее:
Шаг 1: обязательно записать в тетради все числа ряда от 20 до 500 (с шагом 20).
Шаг 2: записать последовательно слагаемые — пары чисел: первого с последним, второго с предпоследним и т.д. и посчитать их суммы.
Шаг 3: посчитать «сумму сумм» и найти сумму всего ряда.
Как видим, это более компактная и эффективная методика: число 3 — также член последовательности Фибоначчи
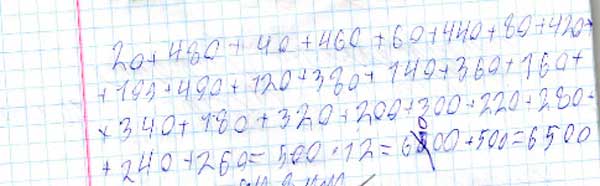
Ответы к стр. 64
Немецкого учёного Кáрла Гáусса называли королём математиков. Его математическое дарование проявилось уже в детстве. Рассказывают, что в трёхлетнем возрасте он удивил окружающих, поправив расчёты своего отца с каменщиками. Однажды в школе (Гауссу в то время было 10 лет) учитель предложил классу сложить все числа от 1 до 100. Пока он диктовал задание, у Гаусса уже был готов ответ. На его грифельной доске было написано: 101 • 50 = 5050.
389. Попробуйте догадаться, как Карл Гаусс складывал числа от 1 до 100.
Он складывал первое и последнее число (1 + 100 = 101), затем второе и предпоследнее число (2 + 99 = 101) и так далее до 50 + 51 = 101. Если 100 чисел разбить на пары, то получится 100 2 = 50 пар, каждая из которых равна 101. То есть 101 • 50 = 5050.
390. Из проволоки длиной 15 м делают обручи длиной 2 м. На сколько об ручей хватит проволоки? Можно ли изготовить 4 обруча? 8 обручей?
15 2 = 7 (ост. 1) — можно сделать 7 обручей и останется ещё 1 м проволоки
О т в е т: хватит на 7 обручей, 4 обруча можно изготовить, а 8 — нельзя.
391. Вычислите, выбирая удобный порядок выполнения действий:
а) 937 — (137 + 793); г) (747 + 896) — 236;
б) (654 + 289) — 254; д) (348 + 252) — 299;
в) 854 + (249 — 154); е) (227 + 358) — (127 + 258).
а) 937 — (137 + 793) = 937 — 137 — 793 = (937 — 137) — 793 = 800 — 793 = 7;
б) (654 + 289) — 254 = 654 + 289 — 254 = (654 — 254) + 289 = 400 + 289 = 689;
в) 854 + (249 — 154) = 854 + 249 — 154 = (854 — 154) + 249 = 700 + 249 = 949;
г) (747 + 896) — 236 = 747 + 896 — 236 = 747 + (896 — 236) = 747 + 660 = 1407;
д) (348 + 252) — 299 = 600 — 299 = 301;
е) (227 + 358) — (127 + 258) = 227 + 358 — 127 — 258 = (227 — 127) + (358 — 258) = 100 + 100 = 200.
392. На одной грядке посадили 30 кустов клубники, а на другой k кустов. Погибло 6 кустов. Сколько кустов клубники осталось на грядках? Составьте выражение для решения задачи и найдите его значение при k = 26; 35.
1) 30 + k (к.) — посадили всего
2) (30 + k) — 6 = 30 + k — 6 = 24 + k (к.) — осталось
3) при k = 26: 24 + 26 = 50 (к.)
4) при k = 35: 35 + 24 = 59 (к.)
О т в е т: при k = 26 осталось 50 кустов, при k = 35 осталось 59 кустов.
393. Найдите значение выражения, предварительно упростив его:
а) (b + 179) — 89 при b = 56; 75;
б) (839 + с) — 239 при с = 37; 98;
в) (256 — х) — 156 при x = 44; 87;
г) 238 — (38 + α) при α = 78; 0.
а) (b + 179) — 89 = b + 179 — 89 = b + 90,при b = 56: 56 + 90 = 146,
при b = 75: 75 + 90 = 165;
б) (839 + с) — 239 = 839 + с — 239 = 600 + с,
при с = 37: 600 + 37 = 637,
при с = 98: 600 + 98 = 698;
в) (256 — х) — 156 = 256 — х — 156 = 100 — х,
при x = 44: 100 — 44 = 56,
при х = 87: 100 — 87 = 13;
г) 238 — (38 + α) = 238 — 38 — α = 200 — α,
при α = 78: 200 — 78 = 122,
при α = 0: 200 — 0 = 200.
394. Найдите значение выражения:
1) 34 • 27 + 1638 : 39; 3) (321 — 267) • (361 — 215) : 219;
2) 32 • 37 — 3293 : 37; 4) (123 + 375) • 24 : (212 — 129).
1) 34 • 27 + 1638 39 = 918 + 42 = 960;
2) 32 • 37 — 3293 37 = 1184 — 89 = 1095;
3) (321 — 267) • (361 — 215) 219 = 54 • 146 219 = 7884 219 = 36;
4) (123 + 375) • 24 (212 — 129) = 498 • 24 83 = 11 952 83 = 144.
395. Решите уравнение:
а) 395 + х = 864; в) 300 — у = 206; д) 166 = m — 34;
б) z + 213 = 584; г) t — 307 = 308; е) 59 = 81 — k.
а) 395 + х = 864,х = 864 — 395,х = 469;
б) z + 213 = 584,z = 584 — 213,z = 371;
в) 300 — у = 206,
300 — 206 = уу = 94;
г) t — 307 = 308,t = 308 + 307,t = 615;
д) 166 = m — 34,
166 + 34 = m,m = 200;
е) 59 = 81 — k,k = 81 — 59,k = 22.
396. Решите уравнение и выполните проверку:
а) (х — 87) — 27 = 36; б) 87 — (41 + у) = 22.
а) (х — 87) — 27 = 36,х — 87 = 36 + 27,х — 87 = 63,х = 63 + 87,х = 150
Проверка:
(150 — 87) — 27 = 36,
63 — 27 = 36,
36 = 36;
б) 87 — (41 + у) = 22,
87 — 22 = 41 + у,
65 = 41 + у,у = 65 — 41,у = 24
Проверка:
87 — (41 + 24) = 22,
87 — 65 = 22
22 = 22.
| ← Предыдущая | Следующая → |
§5. Обыкновенные дроби
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294





















