§8. Инструменты для вычислений и измерений
689
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
Ответы к стр. 29
148. Выясните, какое из чисел больше, и запишите ответ с помощью знака >:
а) 0 или 18; г) 11 871 или 11 859;
б) 74 или 23; д) 2 613 008 или 2 613 001;
в) 147 или 174; е) 6 756 540 623 или 6 756 540 633.
Прочитайте получившиеся неравенства.
а) 0 < 18 — ноль меньше восемнадцати;
б) 74 > 23 — семьдесят четыре больше двадцати трёх;
в) 147 < 174 — сто сорок семь меньше ста семидесяти четырёх;г) 11 871 > 11 859 — одиннадцать тысяч восемьсот семьдесят один больше одиннадцати тысяч восьмиста пятидесяти девяти;д) 2 613 008 > 2 613 001 — два миллиона шестьсот тринадцать тысяч восемь больше двух миллионов шестиста тринадцати тысяч одного;е) 6 756 540 623 < 6 756 540 633 — шесть миллиардов семьсот пятьдесят шесть миллионов пятьсот сорок тысяч шестьсот двадцать три меньше шести миллиардов семисот пятидесяти шести миллионов пятьсот сорока тысяч шестисот тридцати трёх.
149. В числах стёрли несколько цифр и вместо них поставили звёздочки. Выясните, какое из чисел больше, и запишите ответ с помощью одного из знаков > или <:а) 71*** или 75***; б) *3*** или *8*.
а) 71*** < 75***;
б) *3*** > *8*.
150. Прочитайте записи:
а) 17 < 18 < 20; б) 346 < 358 < 400.
а) 17 < 18 < 20 — восемнадцать больше семнадцати и меньше двадцати;
б) 346 < 358 < 400 — триста пятьдесят восемь больше трёхсот сорока шести и меньше четрёхсот.
151. Назовите все натуральные числа, которые лежат между:
а) 11 и 19; б) 2089 и 2091.
Есть ли натуральное число между 6077 и 6078?
а) 12, 13, 14, 15, 16, 17, 18;
б) 2090.
Нет — число 6077 предшествует числу 6078.
152. Запишите с помощью двойного неравенства:
а) число 10 больше, чем 5, и меньше, чем 15;
б) число 11 меньше, чем 18, и больше, чем 8;
в) число 21 меньше, чем 28, а число 28 меньше, чем 45.
а) 5 < 10 < 15;
б) 8 < 11 < 18;
в) 21 < 28 <45.
153. Отметьте на координатном луче все натуральные числа, которые:
а) меньше 9; б) больше 10, но меньше 14.
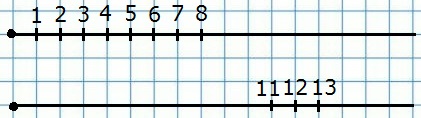
154. Я задумал число, оканчивающееся цифрой 5. Оно больше, чем 210, и меньше, чем 220. Какое это число?
Это число 215: 210 < 215 < 220.
155. В следующей таблице указан рост учащихся. Назовите их фамилии: а) в порядке возрастания их роста; б) в порядке убывания их роста.
| № | Фамилия | Рост, см | № | Фамилия | Рост, см | |
| 1 | Антонов | 124 | 4 | Гришин | 123 | |
| 2 | Борисов | 135 | 5 | Дёмина | 136 | |
| 3 | Воронина | 127 | 6 | Ермилова | 141 |
а) Гришин, Антонов, Воронина, Борисов, Дёмина, Ермилова;
б) Ермилова, Дёмина, Борисов, Воронина, Антонов, Гришин.
156. Верно ли, что:
а) 341 + 569 = 910; г) 98 • 57 = 23 790 : 78;
б) 25 • 42 = 10 500; д) 23 • 27 < 630;
в) 192 : 32 = 38 — 32; е) 1288 : 56 > 40?
а) 341 + 569 = 910 — верно, 910 = 910;
б) 25 • 42 = 10 500 — неверно, 1050 < 10 500;
в) 192 32 = 38 — 32 — верно, 6 = 6;
г) 98 • 57 = 23 790 78 — неверно, 5586 > 305;
д) 23 • 27 < 630 — верно, 621 < 630;
е) 1288 56 > 40 — неверно, 23 < 40.
| ← Предыдущая | Следующая → |
Сравнение натуральных чисел
Давайте рассмотрим данное действие на простых примерах. Если на дереве сидит стая, которая состоит из 7 птиц, а другом дереве сидит стая из 5 десятка птиц, то такие стаи можно считать разными, потому что они не похожи друг на друга. Таким образом можно сделать вывод о том, что данная непохожесть и является сравнением.
В процессе сравнение натуральных чисел может быть проведена такая же проверка по сходству. Если подразумевать под сравнением натуральных чисел действие, то его итогом могут служить следующие исходы:
- Равенство. Данный случай считается вероятным тогда, когда числа являются равными.
- Неравенство. Данный случай считается вероятным тогда, когда числа являются неравными.
Когда получается неравенство — значит, одно из чисел является большим или же меньшим в отношении другого. Это увеличивает диапазон действий, которые можно совершать с натуральными числами.
§3. Умножение и деление натуральных чисел
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
Повторение изученной информации
Запись является неравенством тогда, когда содержит математические выражения, между которыми стоит знак «>» и «<». К примеру, 5 > 4 является неравенством, 2 < 7 также является неравенством. 2 + 3 < 7 также будет являться неравенством.
Неравенства, как и равенства, могут быть как неверными (например, 5 > 8 является неверным неравенством), так и верными (2 < 9 является верным неравенством).
Нестрогое неравенство может предполагать случай равенства правой и левой частей неравенства. Например, является верным неравенством.
Также, для того чтобы записать неравенство двух натуральных чисел, может использоваться знак . Знак M будет читаться как «не равно». К примеру, форма записи будет означать то, что a не равно b. Обычно, если нет оговорок, то понятие неравенства соотносится только с записями со знаками «>» и «<», «» и «».
Неравенство и знаки неравенства.
Чтобы не писать словами больше, меньше или равно в математике придумали обозначения. Больше (>), меньше (<), равно (=). Например, 3 больше 2 математическая запись будет выглядеть так 3>2. Или 6 меньше 10, мы запишем как 6<10. 8 равно 8, запишем 8=8.
Выражения 3>2, 6<10 и 8=8 называются в математики неравенствами.
Такая запись 2<3<4 называется двойным неравенством.
Вопросы к теме:Назовите наименьшее натуральное число?
Ответ: единица.
Назовите наибольшее натуральное число?
Ответ: натуральный ряд чисел бесконечен, поэтому наибольшего натурального числа не существует.
Какое из чисел больше шестизначное или семизначное число?
Ответ: семизначное число больше шестизначного.
Разобраны примеры с ответами на типичные задания темы.Пример №1:
Прочитайте неравенство: а) 5<12 б) 6>1 в) 7=7
Ответ: а) пять меньше двенадцати б) шесть больше одного в) семь равено семи.
Пример №2:
Запишите неравенство: а) 4 меньше 8 б) 10 больше 9 в) 11 равно 11.
Ответ: а) 4<8 б) 10>9 в) 11=11.
Пример №3:
Верны ли неравенства? Проверьте знаки сравнения: а) 5<6 б) 7<3 в) 22>23 г) 5=55
Ответ: а) верно б) неверно в) неверно г) неверно.
Пример №4:
Сравните числа, поставьте правильно знаки неравенства (<, >, =): а)3 и 3 б)4 и 9 в)8 и 3
Ответ: а) 3=3 б) 4<9 в) 8>3
Пример №5:
Посмотрите на рисунок и составьте неравенство.
 Ответ: 10>2 или 2<10.
Ответ: 10>2 или 2<10.
Способы сравнения натуральных чисел.
Рассмотрим натуральный ряд чисел.
1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, …
1) Всегда числа, стоящие справа в натуральном ряду больше чисел, стоящих слева.
Например, сравним числа 7 и 9. Число 9 стоит правее числа 7, следовательно, число 9 больше 7.
Единица, является самым маленьким натуральным числом.
Любое натуральное число больше нуля.
2) Всегда больше то натуральное число, у которого разрядов больше.
Сравним два числа 45 и 190. Сразу понятно, что число 190 больше числа 45. Мы сделали такой вывод потому, что число 190 является трехзначным числом, а 45 – двухзначным числом. У числа 190 есть разряд сотен, десятков и единиц, а у числа 45 только разряд десятков и единиц.
3) Если количество разрядов одинаково, то мы будем сравнивать величины цифр разрядов, начиная с высшего разряда (слева направо).
Например, сравним числа 478 и 399. Оба числа являются трехзначными, поэтому подробно рассмотрим высший разряд сотен. У первого числа 478 разряд сотен равен 4, а у второго числа 399 разряд сотен равен 3. Следовательно, первое число 478 больше второго числа 399, потому что 4 больше 3.
Если высшие разряды одинаковые мы сравниваем следующий меньший разряд цифр.
Сравним числа 7890 и 7860. Начинаем сравнивать высший разряд единиц тысяч он у обоих чисел равен 7. Следующий разряд сотен, также равен у обоих чисел 8. А вот разряд десятков различен. У первого числа 7890 разряд десятков равен 9, а у второго числа 7860 равен 6. Далее делаем вывод, первое число 7890 больше 7860, потому что разряд десятков у первого числа больше чем у второго. Проще сказать, 9 больше 6.
4) Если при сравнении все цифры разрядов двух натуральных чисел одинаковы, значит числа равны.
Например, сравним числа 4890765 и 4890765. Видно, что у обоих чисел все цифры разрядов одинаковы, следовательно, они равны.
Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Меньше или больше — Урок 2 — НАТУРАЛЬНЫЕ ЧИСЛА И ШКАЛЫ — НАТУРАЛЬНЫЕ ЧИСЛА
Основная дидактическая цель урока: учить сравнивать натуральные числа и записывать результат сравнения в виде неравенства, читать и записывать двойные неравенства.
Ход урока
I. Организационный момент
II. Устный счет
1. Индивидуальная работа у доски.
Задание 1. В каждой группе подчеркните ту точку, которая лежит левее всех.
А(64) В(61) С(16)
К(41) Е(14) Р(40)
М(6) Y(2) D(12)
Задание 2. В каждой группе подчеркните ту точку, которая лежит правее всех.
E(76) O(56) K(87)
P(32) A(23) B(31)
М(61) T(16) С(45)
Задание 3. Сравните.
766 и 677
3434 и 3344
2154 и 999
2. Фронтальная работа (учащиеся работают вместе с учителем).
1) Найдите сумму чисел 620 и 40. (660.)
2) Найдите разность чисел 620 и 40. (580.)
3) Число 15 увеличьте в 6 раз. (80.)
4) Число 48 уменьшите на 8. (40.)
5) Что больше — сумма 13 и 1 или их произведение? (Сумма.)
6) Что меньше — произведение 64 и 0 или их сумма? (Произведение.)
7) Сколько натуральных чисел лежит между точкой A(67) и точкой B(69)? (Одно.)
![]() От точки М с координатой 59 отложили семь единичных отрезков вправо. Назовите координату полученной точки. (66.)
От точки М с координатой 59 отложили семь единичных отрезков вправо. Назовите координату полученной точки. (66.)
3. Коллективная проверка индивидуальной работы у доски.
4. Решите задачу.
В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных (одну девочку и одного мальчика)?
— Что можете сказать про эту задачу?
— Сколькими способами можно выбрать на дежурство одного мальчика? (15.)
— Сколько вариантов выбора девочки существует для каждого мальчика? (10.)
— Сколько же вариантов выбора двух дежурных существует? (15 ∙ 10 = 150.)
III. Определение темы урока
Сегодня на уроке мы будем учиться сравнивать числа, записывать и читать неравенства.
IV. Работа по теме урока
1. Вместо звездочки поставьте цифру так, чтобы неравенство было верным. Объясните свой выбор.
617* < 6171
3454 >34*9
3128 < 312*
2785 < 27*0
2. Запишите в тетрадь все натуральные числа, которые на координатном луче находятся между числами 894 и 901.
3. В числах стерли несколько цифр, а вместо них поставили звездочки. Сравните эти числа, если возможно. Объясните свое решение.
63*** и 61***
28* и 1***
**1* и 99*
V. Работа по учебнику
1. С. 29, № 149 (работа в паре).
2. С. 29, № 150.
— Как называются эти записи?
— Как читаются двойные неравенства?
— Прочитайте.
3. С. 29, № 152.
Проверка
5 < 10 < 15
8 < 11 < 18
21 < 28 < 45
— Прочитайте двойные неравенства.
— Придумайте свое задание с двойным неравенством.
4. С. 29, № 153.
— Прочитайте задание.
— Сколько координатных лучей надо начертить?
VI. Работа над задачей
С. 30, № 164.
— Прочитайте задачу.
— Что требуется узнать в задаче?
— Что нужно знать для того, чтобы узнать производительность каждого рабочего?
— Можно ли узнать время работы?
— Что можно узнать, зная всю работу и время?
— Составьте план решения задачи.
— Решите задачу.
1) 10 — 2 = 8 (ч.) — время работы.
2) 1248 : 8 = 156 (д.) — 13 рабочих в час.
3) 156 : 13 = 12 (д.) — производительность одного рабочего.
VII. Самостоятельная работа
Вариант 1
С. 31, № 167 (1 и 3).
4428: 123 — 33
4428 : 123 = 36
36 — 33 = 3
Ответ: 3.
(8032 — 595) : 37
8032 — 595 = 7437
7437 : 37 = 201
Ответ: 201.
Вариант 2
С. 31, № 167 (2 и 4).
4000 — 3249 : 57
3249 : 57 = 57
4000 — 57 = 3943
Ответ: 3943.
10 486 : (2455 — 2357)
2455 — 2357 = 98
10 486 : 98 = 107
Ответ: 107.
VIII. Рефлексия
— Что бы вы хотели повторить на следующем уроке?
— Как читают двойные неравенства?
— Как сравнивать числа с одинаковым количеством знаков?
Домашнее задание
С. 31, № 173, 174; с. 32, № 179.
ПредыдущаяСледующая
Двойные и тройные неравенства
Математике известно, что 5 < 12, а 12 < 35. Два данных неравенства возможно показать в форме одного двойного неравенства. Данная запись обладает следующим видом: 5 < 12 < 35. Видно, что в процессе записи двойного неравенства получится три неравенства, которые можно записать как 5 < 12, 12 < 35 и 5 < 35.
В форме двойного неравенства можно сделать запись в процессе сравнения трех чисел. Когда нужно совершить сравнение 76, 512 и 10, у нас может получиться целых три неравенства 76 < 512, 76 > 10, 512 > 10. Данные неравенства также можно записать как одно, но двойное: 10 < 76 < 512.
Точно так же можно совершить и тройные, и четверные, и другие неравенства. Так, известно, что 5 < 16, 16 < 305, 305 < 1001, 1001 < 3214. Тогда можно показать запись в следующем виде: 5 < 16 < 305 < 1001 < 3214. Нужно проявлять крайнюю внимательность тогда, когда составляются двойные неравенства, потому что можно составить их неверно, что повлечет за собой неверное решение задачи.































