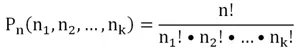3 класс. окружающий мир. плешаков, новицкая. рабочая тетрадь. часть 1. страницы 70, 71, 72, 73

Метод шаров и перегородок

9. Сколькими способами можно разложить 10 шаров в 4 коробки? Предполагается, что некоторые коробки могут оказаться пустыми.

Решение.

Рассмотрим 10 шаров:

Будем «раскладывать шары  по коробкам», ставя перегородки.

Например, так:

В этом примере в первой коробке  3 шара, во второй  — 2, в третьей — 4, и в четвертой — 2. Переставляя шары и перегородки, мы получаем различные комбинации шаров в коробках. Например, переставив последний шар в первой коробке и первую внутреннюю перегородку, мы получим такую комбинацию:

Таким образом, мы получаем различное число шаров в коробках, комбинируя позиции 10-ти шаров и 3-х внутренних перегородок. Чтобы определить, сколько различных комбинаций мы можем получить, нам нужно найти число сочетаний из 13 по 3. (Или, что то же самое, что число сочетаний из 13 по 10.) Столько способов выбрать 3 места для перегородок из 13 возможных позиций. Или, что то же самое, 10 мест для шаров.

10. Сколько решений имеет уравнение в целых неотрицательных числах?

Решение.

Так как переменные могут принимать только целые неотрицательные значения, следовательно, у нас есть 10 переменных, и они могут принимать значения 0, 1, 2, 3 и 4. Представим, что у нас есть 10 коробок (это переменные), и мы должны разложить по этим коробкам 4 шара. Сколько шаров попадет в коробку, таково значение соответствующей переменной. Если у нас 10 коробок, следовательно, 10-1=9 внутренних перегородки. И 4 шара. Всего 13 мест. Нам надо расположить на этих 13 местах 4 шара. Число таких  возможностей:

В общем случае, если нам нужно разложить шаров в коробок, мы получаем комбинации из шаров  и внутренней перегородки. И число таких комбинаций равно числу сочетаний из по .

В этой задаче мы имели дело с сочетаниями с повторениями.

Что готовят ученикам уроки математики

Учебный курс за третий класс познакомит школьников с методами решения задач и примеров в несколько действий, кроме этого они изучат таблицу умножения и деления в пределах двух десятков, а также рассмотрят единицы стоимости, массы и времени. Третьеклассники освоив программу научатся:

1. Сравнивать различные величины.
2. Решать и составлять текстовые задачи.
3. Чертить отрезок и измерять его длину.
4. Находить значение числовых выражений.
5. Обозначать буквами геометрические фигуры.

Уроки дисциплины учат юных школьников анализировать, сопоставлять, сравнивать и делать выводы. Эти навыки крайне необходимы для успешного изучения предмета в средней и старшей школе.

Размещения

Пусть в футбольном турнире участвуют 6 команд. Нам предлагают угадать те команды, которые займут призовые места (то есть первые три места). Сколько вариантов таких троек существует?

Сначала запишем ту команду, которая выиграет турнир. Здесь есть шесть вариантов, по количеству участвующих команд. Запишем эти варианты:

Далее выберем один из вариантов и для него укажем серебряного призера соревнований. Здесь есть только 5 вариантов, ведь 1 из 6 команд уже записана на 1-ом месте:

Такую пятерку можно записать для каждого из шести вариантов того, кто станет чемпионом. Получается, что всего есть 6•5 = 30 пар «чемпион – серебряный призер». Наконец, для одной такой пары можно записать 4 варианта того, кто окажется третьим (две команды писать нельзя, так как они уже записаны на первых двух строчках):

Для каждой пары можно записать 4 тройки призеров. Так как число пар «чемпион – вице-чемпион» равно 6•5 = 30, то число троек составит 6•5•4 = 120.

В данном случае из некоторого множества команд мы выбрали несколько и расположили их в каком-то порядке. То есть мы выбрали упорядоченное множество. В комбинаторике оно называется размещением.

Если общее число команд обозначить как n (в этом примере n = 6), а количество упорядочиваемых команд равно k, то количество таких размещений в комбинаторике обозначается как

В примере с командами количество размещений равнялось 120:

Читается эта запись как «число размещений из 6 по 3 равно 120».

Для нахождения этого числа мы перемножили k (3)множителей. Первый из них был равен n(6), так как каждая из n команд могла занять первая место. Второй множитель был равен (n– 1), так как после определения чемпиона мы могли поставить на вторую позицию одну из (n– 1) команд. Третий множитель был равен (n– 2). По этой логике каждый следующий множитель будет меньше предыдущего на единицу. Например, чтобы вычислить число размещений из 7 по 4, надо перемножить 4 множителя, первый из которых равен 7, а каждый следующий меньше на 1:

Однако математически удобнее представлять это произведение как отношение двух факториалов. Для этого умножим количество размещений на дробь 3!/3!, равную единице. Естественно, число размещений из-за умножения на единицу не меняется:

Число 3 в данном случае можно получить, если из 7 вычесть 4. В общем случае из числа n надо вычесть число k. Тогда формула для вычисления количества размещений примет вид:

Пример. В программе 8 «А» класса 12 различных предметов. В понедельник проводится 5 занятий подряд. Сколько существует вариантов расписаний для класса, если в течение понедельника нельзя проводить два одинаковых урока?

Решение. Для составления расписания нужно выбрать 5 предметов и расставить их по порядку. Поэтому нам необходимо найти размещение из 12 по 5:

Ответ: 95040

Пример. В вагоне 10 свободных мест. В него зашло 6 пассажиров. Сколькими способами они могут расположиться в вагоне?

Решение. Из десяти мест надо выбрать шесть и указать для каждого, какому пассажиру оно соответствует. То есть каждый вариант рассадки пассажиров – это размещение из 10 по 6. Найдем их количество:

Ответ: 151200

Заметим, что перестановка – это частный случай размещения, когда k = n. Действительно, если нам надо указать тройку призеров турнира, в котором участвуют 6 команд, то мы указываем размещение из 6 по 3. Но если мы указываем для каждой из 6 команд, какое место она займет в чемпионате, то это размещение из 6 по 6. С другой стороны, это расстановка одновременно является и перестановкой 6 команд. Убедимся, что в этом частном случае формула для подсчета количества размещений покажет тот же результат, что и формула для перестановок

Для примера с 6 командами это будет выглядеть так:

Здесь мы использовали тот факт, что факториал нуля принимается равным единице. Данное рассуждение можно, наоборот, использовать для того, чтобы доказать, что факториал нуля – это единица.

Ответы к страницам 70, 71, 72 и 73

Другие решебники 3 класс:

• Математика
• Русский язык
• Английский язык
• Окружающий мир
• Литературное чтение

Луг — царство цветов и насекомых

1. Найди на рисунке учебника (с. 106 — 107) цветы и насекомых. Впиши их названия в таблицу.Цветы и насекомые луга

Цветы	Насекомые
Колокольчик, тысячелистник, нивяник, мышинный горошек.	Кобылка, цветочные мухи, навозник обыкновенный, шмель, пчела, махаон, кузнечик, голубянка.

2. 1. Определите растения луга, изображённые в Приложении. Вырежите рисунки и наклейте их в соответствующие окошки.

Сравните виды растений в каждой паре: найдите черты сходства и различий.
Отметьте (закрасьте кружок) растения, которые вы встречали в природе.

2. Определите насекомых луга, изображённых на рисунке. Подпишите названия. При необходимости используйте слова для справок.

желтушка луговая	жук-могильщик	зорька
бронзовка золотистая	пестрянка	навозник обыкновенный

Подумайте, на какие две группы можно разделить этих насекомых. Красным карандашом (бабочки) обведите представителей одной группы, зелёным (жуки) — представителей другой. Проверьте себя по Приложению.
Отметьте (закрасьте кружок) насекомых, которых вы видели в природе.

3. Самостоятельно или с помощью рисунка учебника (с. 106 — 107) составьте схемы цепей питания в луговом сообществе.
а) колокольчик → кобылка → трясогузка
б) тысячелистник → журчалка → коростель
в) нивяник → кузнечик → ящерица

4. Нарисуй схему круговорота веществ на лугу. Возьми за образец схему круговорота веществ в лесном сообществе (с. 102 учебника).

Расскажи по схеме о круговороте веществ на лугу. Сравни его с круговоротом веществ в лесу.

5. Запиши названия обитателей лугов твоего края (не менее трёх в каждом пункте).
Растения: клевер, одуванчик, мать-и-мачеха, ромашка.
Животные: змеи, трясогузка, полевая мышь, ящерица.
Грибы: сыроежка, лисички, шампиньоны.

6. В книге «Зелёные страницы» прочитай на выбор рассказ «Тысячелистник» или «Кислый, но вкусный». Запиши 2—3 интересных факта.Если щавелю оторвать листок, то на этом месте вскоре вырастет новый.В листьях щавеля содержится особое вещество — щавелевая кислота.

7. В книге «Великан на поляне» прочитай рассказ «Не ловите насекомых для коллекций». Найди в рассказе и кратко запиши ответы на вопросы.
Почему коллекции насекомых, которые раньше собирали школьники, приносили больше вреда, чем пользы?Школьники собирали много различных насекомых, в том числе и редких, тем самым наносили вред природе. Большая часть коллекций потом просто выбрасывалась.

Как лучше изучать насекомых тому, кто ими интересуется?Делать фотографии и рисунки насекомых, вести дневник наблюдений.

Где можно увидеть настоящие коллекции насекомых, собранные учёными?В зоологических музеях.

• ← предыдущее
• следующее →

Сочетания

Выбирая размещение, мы должны были выбрать из множества несколько объектов и упорядочить их. В частности, мы выбирали три команды из шести и указывали, какая из них будет первой, какая второй, а какая третьей. Поэтому размещения «Локомотив, Зенит, Краснодар» и «Локомотив, Краснодар, Зенит» отличались друг от друга.

Однако порою этот порядок не имеет значения. Так, существует известная лотерея, где предлагается угадать 7 чисел из 49, которые выпадут во время розыгрыша из барабана. При этом порядок их выпадения не играет никакой роли. Игрок, выбирая эти 7 чисел, с точки зрения математики формирует сочетание из 49 по 7.

Количество возможных сочетаний из n по k обозначается буквой С:

Для вычисления количеств сочетаний из n по k сначала найдем количество аналогичных размещений. Оно вычисляется по формуле:

Однако ясно, что, как и в случае с перестановками с повторениями, некоторые сочетания мы посчитали несколько раз. Вернемся к примеру с командами. Если мы выбрали команды Л (Локомотив) , З (Зенит) и К (Краснодар), то мы можем составить ровно 3! = 6 размещений из них:

ЛЗК

ЛКЗ

ЗЛК

ЗКЛ

КЛЗ

КЗЛ

Однако все они соответствуют только одному сочетании – ЛКЗ. Таким образом, считая количество размещений, мы посчитали каждое сочетание не один, а 3! раз. Поэтому для нахождения количества сочетаний в комбинаторике надо поделить число размещений на число перестановок k элементов:

Эта формула связывает важнейшие понятия комбинаторики – перестановки, сочетания и размещения. Подставим в неё формулы для размещений и перестановок и получим:

Пример. Сколько троек призеров турнира можно составить, выбирая три футбольные команды из шести?

Решение. Посчитаем число сочетаний из 6 по 3:

Ответ: 20

Пример. Сколько комбинаций чисел может составить игрок, играющий в лотереи «5 из 36», «6 из 45», «7 из 49»?

Решение. В каждом из этих случаев игрок выбирает сочетание нескольких чисел. Посчитаем их число:

Ответ: 376992; 8145060; 85900584

Пример. На плоскости отмечены 8 точек, причем никакие три из них не лежат на одной прямой. Сколько различных прямых можно провести через них? Сколько треугольников и четырехугольников можно построить с вершинами в этих точках?

Решение. Для того чтобы провести прямую, достаточно выбрать любые 2 точки из 8. Общее количество прямых будет равно числу сочетаний из 8 по 2:

Заметим принципиальную важность того условия, что никакие три точки не лежат на одной прямой. Оно гарантирует, что при выборе двух различных точек мы будем получать различные прямые

Если бы, например, точки АВС лежали бы на одной прямой, то при выборе сочетаний АВ, ВС и АС мы получали бы одну и ту же прямую:

Это же условие гарантирует, что, выбрав любые 3 и 8 точек, мы сможем построить треугольник с вершинами в этих точках, а выбрав 4 точки, получим четырехугольник. Поэтому для подсчета количества треугольников и четырехугольников следует искать число сочетаний по 3 и 4:

Ответ: 28 прямых, 56 треугольников и 70 четырехугольников.

Пример. В одной урне находится 10 различных шаров с номерами от 0 до 9, а в другой – 8 различных шаров с первыми восемью буквами алфавита. По условиям лотереи ведущий вытаскивает из первой урны два шара с числами, а из второй – три шара с буквами. Для победы в лотерее надо угадать выпавшие шары. Сколько комбинаций шаров может выпасть в игре?

Решение. Посчитаем отдельно, сколькими способами можно выбрать 2 шара с цифрами из 10 и 3 шара с буквами из 8:

По правилу умножения мы должны перемножить эти числа, чтобы найти общее количество возможных вариантов:

56•45 = 2520

Ответ: 2520

Заметим, что выбирая, например, сочетание из 49 по 7, мы одновременно выбираем и сочетание из 49 по 49 – 7 = 42. Действительно, игрок, обводящий в кружок в лотерейном билете свои 7 счастливых чисел, одновременно и определяет остальные 42 числа, какие числа он НЕ считает счастливыми. Для наглядности запишем число сочетаний в обоих случаях:

Получили одну и ту же дробь, в которой отличается лишь последовательность множителей в знаменателе. Можно показать, что и в общем случае число сочетаний из n по k совпадает с количеством сочетаний из n по (n– k):

Какое количество символов входит в комбинацию?

Количество символов входит в определение комбинации в данной игре. В данном контексте комбинация — это набор из 6 символов.

Символы могут быть любыми, включая буквы, цифры и специальные символы. Например, комбинацией может быть последовательность букв «abc123» или «xy#00!».

Всего возможно составить огромное количество комбинаций из 6 символов. Для того чтобы понять, сколько именно, нужно использовать комбинаторику.

В данном случае используется комбинация без повторений символов, то есть символы в комбинации не могут повторяться.

Для вычисления количества таких комбинаций можно использовать формулу:

n! / (n — k)!

где n — общее количество символов (букв, цифр, специальных символов), а k — количество символов в комбинации.

Например, если имеется 26 букв английского алфавита и 10 цифр, то общее количество символов будет равно 26 + 10 = 36. А если в комбинации должно быть ровно 6 символов, то формула будет выглядеть следующим образом:

36! / (36 — 6)! = 36! / 30!

Здесь знак «!» обозначает факториал — произведение всех натуральных чисел от 1 до данного числа.

Результатом вычислений будет очень большое число, которое покажет, сколько всего комбинаций из 6 символов можно составить в данном случае.

Можно представить это число в виде графического примера. Например, рассмотрим таблицу, в которой каждой комбинации из 6 символов будет соответствовать одна строка:

Комбинация
abc123
abc12#
abc1!6
…
zzy#00

Таких строк будет очень много, и количество возможных комбинаций будет определяться формулой, описанной выше.

Комбинаторика и ее основные принципы

Очень часто приходится решать задачи, в которых надо посчитать количество возможных вариантов для той или иной ситуации. Например, сколько позиций может возникнуть на шахматной доске после первого хода обоих игроков? Сколько разных паролей длиною в десять символов можно записать, если ни один символ не использовать дважды? Сколько разнообразных комбинаций чисел может выпасть при игре в лотерею «6 из 49»? На все эти вопросы помогает ответить специальный раздел математики, называемый комбинаторикой. Почти всегда комбинаторную задачу можно сформулировать так, чтобы ее вопрос начинался словами «сколькими способами…».

Очевидно, что если в конечном множестве содержится n элементов, то есть ровно n способов выбрать один из них.

Пример. В классе 15 человек. Сколькими способами учитель может назначить одного из них ответственным за чистоту доски?

Ответ. Таких способов ровно 15.

В комбинаторике существует два основных правила. Первое из них называется правилом сложения.

Несмотря на формулировку, по сути это очень простое правило.

Пример. В магазине продается 14 телевизоров Panasonic и 17 телевизоров Sony. Петя хочет купить один телевизор. Сколько у него вариантов покупки?

Решение. По правилу сложения Петя может выбрать один из 14 + 17 = 31 телевизоров.

Ответ: 31 телевизор.

Особое значение имеет второе правило, которое называют правилом умножения.

Проиллюстрируем это правило.

Пример. В секции бадминтона 15 мальчиков и 20 девочек. Тренер должен отправить на соревнования смешанную пару. Сколько вариантов действий у него?

Решение. Тренер может составить 15•20= 300 разнополых пар из своих воспитанников.

Ответ: 300

Пример. Пете нужно купить технику для компьютера. В магазине продается 20 различных клавиатур, 25 моделей геймпадов и 30 компьютерных мышей. Купить надо по одному экземпляру каждого из этих устройств. Сколько вариантов покупки есть у него?

Решение. Сначала подсчитаем число возможных пар «клавиатура-геймпад». Их количество равно 20•25 = 500. Теперь составим «тройку» из одной из 500 пар и одной из 30 мышей. Число троек равно 500•30 = 15000.

Ответ: 15000

Правила сложения и умножения можно комбинировать.

Пример. Сколько слов не более чем из трех букв можно составить, используя алфавит, содержащий ровно 30 букв?

Решение. Очевидно, что слов из одной буквы можно составить ровно 30. Количество двухбуквенных слов равно количеству пар, которые можно составить из этих букв, то есть 30•30 = 900. Трехбуквенных слов можно составить 30•30•30 = 27000. Всего же слов длиною не более 3 букв будет

30 + 900 + 27000 = 27930

Ответ: 27930

Далее мы изучим основные понятия комбинаторики – перестановки, размещения, сочетания.

Перестановки с повторениями

До этого мы рассматривали случаи, когда все переставляемые объекты были различными. Однако порою некоторые из них не отличаются друг от друга. Пусть на полке надо расставить 3 книги, но две из них одинаковые. Сколько тогда существует перестановок? Общее число перестановок 3 книг составляет 3! = 6:

Здесь одинаковые книги отмечены как А и А1. Очевидно, что 1-ый и 2-ой варианты (А1АБ) и (АА1Б) на самом деле не отличаются друг от друга. В них отличается лишь порядок одинаковых книг А и А1. В первом случае за А1 следует А, а во втором, наоборот, за А следует А1. Тоже самое можно сказать про варианты 3 и 4, 5 и 6. Получается, что все возможные перестановки можно разбить на группы, в которых находятся «перестановки-дубликаты»:

А1АБ и АА1Б

А1БА и АБА1

БА1А и БАА1

В каждой группе находится ровно по два «дубликата». Почему именно по два? Это число равно количеству перестановок одинаковых книг. Так как одинаковых томов 2, а Р₂ = 2, то в каждой группе по 2 «дубликата». Действительно, если бы мы «убрали» с полки все книги, кроме повторяющихся, то там осталось бы только 2 одинаковых тома, которые можно переставить двумя способами.

Для того чтобы найти количество «оригинальных» перестановок, надо их общее количество поделить на число дубликатов в каждой группе.

6:2 = 3

Пусть теперь надо расставить 4 книги, из которых 3 одинаковы. Обозначим тома как А, А1, А2 и Б. Всего можно записать 4! = 24 перестановки. Однако каждые 6 из них будут дублировать друг друга. То есть их можно разбить на группы, в каждой из которых будет 6 идентичных «дубликатов»:

1-ая группа: БАА1А2, БАА2А1, БА1АА2, БА1А2А, БА2АА1, БА2А1А

2-ая группа: АБА1А2, АБА2А1, А1БАА2, А1БА2А, А2БАА1, А2БА1А

3-ая группа: АА1БА2, АА2БА1, А1АБА2, А1А2БА, А2АБА1, А2А1БА

4-ая группа: АА1А2Б, АА2А1Б, А1АА2Б, А1А2АБ, А2АА1Б, А2А1АБ

И снова для подсчета числа оригинальных перестановок надо из общее число расстановок поделить на количество дубликатов в каждой группе:

Р₄/Р₃ = 4!/3! = 24/6 = 4

Для обозначения перестановок с повторениями используется запись

Р_n(n₁, n₂, n₃,… n_k)

где n – общее количество объектов, а n₁, n₂, n₃,… n_k – количество одинаковых элементов. Например, в задаче с 4 книгами мы искали величину Р₄(3, 1), потому что всего книг было 4, но они были разбиты на две группы, в одной из которых находилось 3 одинаковых тома (буквы А, А1, А2), а ещё одна книга (Б) составляла вторую группу. Мы заметили, что для вычисления числа перестановок с повторениями надо общее число перестановок делить на количество дублирующих перестановок. Формула в общем случае выглядит так:

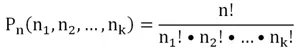
Решение. Вася должен расставить 3 урока испанского и 4 урока английского, тогда n₁ = 3, а n₂ = 4. Общее количество уроков равно 3 + 4 = 7. Тогда

Ответ: 35

Обратите внимание, что для удобства при делении факториалов мы не вычисляли их сразу, а пытались сократить множители. Так как в ответе любой комбинаторной задачи получается целое число, то весь знаменатель дроби обязательно сократится с какими-нибудь множителями в числителе

Пример. У мамы есть 3 яблока, 2 банана и 1 апельсин. Эти фрукты она распределяет между 6 детьми. Сколькими способами она может это сделать, если каждый должен получить по фрукту?

Решение. Всего есть три группы фруктов. В первой находится 3 яблока, поэтому n₁ = 3. Во второй группе 2 банана, поэтому n₂ = 2. В третьей группе только 1 апельсин, поэтому n_k = 1. Общее число фруктов равно 6. Используем формулу:

Ответ: 60

В знаменателе формулы для перестановок с повторениями мы записываем число объектов в каждой группе одинаковых предметов. Так, если переставляются 3 яблока, 2 банана и 1 апельсин, то в знаменателе мы пишем 3!•2!•1!. Но что будет, если в каждой группе будет находиться ровно один уникальный объект? Тогда мы запишем в знаменателе произведение единиц:

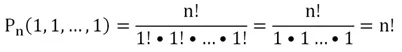
В итоге мы получили ту же формулу, что и для перестановок без повторов. Другими словами, перестановки без повтора могут рассматриваться просто как частный случай перестановок с повторами.

Перестановки

Воспользуемся правилом умножения чтобы ответить на вопрос, «сколькими способами можно построить 7 человек в шеренгу?».

Человека, стоящего первым в шеренге можно выбрать семью способами, второго можно выбрать из оставшихся шести человек, то есть шестью способами. Третьего, соответственно, пятью. И так далее. Последнего можно выбрать единственным способом. Всего получаем способов построить 7 человек в шеренгу.

В общем случае, если мы имеем объектов, которые хотим расположить в определенном порядке (пронумеровать их), то мы получим

способов расположения этих объектов.

Факториалом натурального числа называется произведение всех натуральных чисел от 1 до :

По определению 0!=1; 1!=1.

Перестановкой из предметов называется любой способ нумерации этих предметов (способ расположения их в ряд).

Число перестановок предметов равно .

3. Имеется 10 компьютерных дисков и 10 коробок от них. Найдите вероятность того, что случайным образом уложив диски в коробки, мы обнаружим, что

1. Каждый диск лежит в своей коробке.

2. Хотя бы один диск лежит не в своей коробке.

3. Два определенных диска перепутаны местами, а остальные в своих коробках.

4. Ровно один лежит не в своей коробке, а остальные  — в своих коробках.

Решение.

4. Слово «МАТЕМАТИКА» написали на полоске картона и разрезали полоску на буквы. Найдите вероятность того, что составив все эти буквы случайным образом в ряд, мы снова получим слово «МАТЕМАТИКА».

Сколько буквосочетаний можно составить из букв слова «МАТЕМАТИКА»?

Решение.

Вопросы

1. Вычислите результат целочисленного деления.23 // 7 = 320 // 5 = 42 // 5 = 0123 // 10 = 12— 123 // 10 = -13
2. Вычислите остаток от деления.23 % 7 = 220 % 5 = 02 % 5 = 2123 % 10 = 3
3. Что будет выведено на экран в результате выполнения следующей программы?a = 15 // (16 % 7) b = 34 % a * 5 — 29 % 5 * 2 print(a + b)Ответ: 29
4. Что будет выведено на экран в результате выполнения следующей программы?a = 82 // 3 ** 2 % 7print(a)Ответ: 2

# Получаем переменные b1,q,n
b1 = int(input())
q = int(input())
n = int(input())

# Выводим результат на экран
print(b1 * q ** (n-1))

# Получаем число в сантиметрах и записываем в переменую cm
cm = int(input())

# Переводим сантиметры в метры
m = cm // 100

# Выводим результат на экран
print(m)

# Получаем число школьников и мандаринов записав данные в переменные
sch = int(input())
fru = int(input())

# Выводим результат на экран
print(fru // sch)
print(fru % sch)

# Получаем население и записываем в переменную n
n = int(input())

# Выводим на экран колличество выживших
print(n//2 + n%2)

# Получаем номер места и кладем в переменную n
n = int(input())

# Добавленное к месту 3 оставшихся места и проводим целочисленное деление на количество мест в купе (4)
print((n + 3) // 4)

# Получаем и записываем в переменную кол-во минут
m = int(input())

h = m // 60    # Часы    целочисленное деление
s = m % 60     # Минуты  остаток от деления

# Выводим результат на экран
print(m, "мин - это", h, "час", s, "минут.")

# Получаем число и сохраняем в переменную num
num = int(input())

a = num % 10            # Последняя цифра числа 
b = (num % 100) // 10   # Предпоследняя цифра числа
c = num // 100          # Первая цифра числа

# Выводим результат на экран
print("Сумма цифр =", c + b + a)
print("Произведение цифр =", c * b * a)

# Получаем трехзначное число и сохраняем в переменную abc
abc = int(input())

c = abc % 10            # Последняя цифра числа 
b = (abc % 100) // 10   # Предпоследняя цифра числа
a = abc // 100          # Первая цифра числа

# Выводим перебор всех перестановок цифр
print(a, b, c, sep='')
print(a, c, b, sep='')
print(b, a, c, sep='')
print(b, c, a, sep='')
print(c, a, b, sep='')
print(c, b, a, sep='')

# Получаем число и сохраняем в m
m = int(input())

m1 = m // 1000        # Цифра в позиции тысяч
m2 = (m // 100) % 10  # Цифра в позиции сотен 
m3 = (m // 10) % 10   # Цифра в позиции десятков
m4 = m % 10           # Цифра в позиции единиц

# Выводим результат согласно условиям
print("Цифра в позиции тысяч равна", m1)
print("Цифра в позиции сотен равна", m2)
print("Цифра в позиции десятков равна", m3)
print("Цифра в позиции единиц равна", m4)

Следующий модуль 3: Итоговая работа по условным операторам («Поколение Python»).

архив записей

архив записейВыберите месяц Июль 2021  (2) Май 2021  (2) Май 2020  (2) Апрель 2020  (2) Март 2020  (1) Февраль 2020  (1) Январь 2020  (2) Декабрь 2019  (1) Ноябрь 2019  (2) Октябрь 2019  (9) Сентябрь 2019  (2) Август 2019  (5) Май 2019  (3) Апрель 2019  (2) Март 2019  (2) Февраль 2019  (2) Январь 2019  (2) Декабрь 2018  (4) Ноябрь 2018  (2) Октябрь 2018  (3) Сентябрь 2018  (4) Август 2018  (3) Июль 2018  (5) Июнь 2018  (2) Май 2018  (3) Апрель 2018  (10) Март 2018  (9) Февраль 2018  (3) Январь 2018  (1) Декабрь 2017  (4) Ноябрь 2017  (3) Октябрь 2017  (4) Сентябрь 2017  (6) Август 2017  (1) Июль 2017  (5) Июнь 2017  (13) Май 2017  (2) Апрель 2017  (48) Март 2017  (3) Февраль 2017  (11) Январь 2017  (9) Декабрь 2016  (2) Ноябрь 2016  (9) Октябрь 2016  (3) Сентябрь 2016  (2) Август 2016  (4) Июль 2016  (10) Июнь 2016  (14) Май 2016  (9) Апрель 2016  (26) Март 2016  (5) Февраль 2016  (4) Январь 2016  (16) Декабрь 2015  (6) Ноябрь 2015  (10) Октябрь 2015  (4) Август 2015  (3) Июль 2015  (3) Июнь 2015  (6) Май 2015  (1) Апрель 2015  (8) Март 2015  (10) Февраль 2015  (7) Январь 2015  (7) Декабрь 2014  (5) Ноябрь 2014  (16) Октябрь 2014  (4) Сентябрь 2014  (12) Август 2014  (1) Июль 2014  (8) Июнь 2014  (2) Май 2014  (10) Апрель 2014  (6) Март 2014  (9) Февраль 2014  (8) Январь 2014  (2) Декабрь 2013  (1) Ноябрь 2013  (9) Октябрь 2013  (10) Сентябрь 2013  (13) Июнь 2013  (3) Май 2013  (9) Апрель 2013  (11) Март 2013  (9) Февраль 2013  (8) Январь 2013  (9) Декабрь 2012  (3) Ноябрь 2012  (7) Октябрь 2012  (8) Сентябрь 2012  (12) Август 2012  (5) Июнь 2012  (3) Май 2012  (15) Апрель 2012  (17) Март 2012  (28) Февраль 2012  (23) Январь 2012  (32) Декабрь 2011  (15)

Полезные свойства решебника

Освоение дисциплины довольно сложная задача, с которой многие ученики справляются с трудом. Современная школьная программа и большие нагрузки крайне негативно влияют на качество знаний и успеваемость. В таком случае специалисты рекомендуют использовать «ГДЗ по Математике 3 класс Рабочая тетрадь Школа России Моро, Волкова (Просвещение)». Онлайн-решебник имеет правильные и максимально понятные ответы. Они расписаны практически ко всем номерам учебного издания и помогут:

• без ошибок выполнить домашнюю работу;
• понять и разобрать сложную тему;
• на «отлично» подготовиться к предстоящему уроку;
• сэкономить время и силы на поиск необходимой информации.

Систематическое использование ГДЗ имеет только положительные результаты, которые наилучшим образом скажутся на учёбе, плюс ко всему школьник всегда будет во всеоружии перед любой проверкой знаний в классе.